矩阵乘法的五种理解 - Strang MIT 18.06 线性代数精髓 1
在本系列中,我们用彩色 Latex 笔记记录下 MIT 18.06 Gilbert Strang 教授经典的线性代数课程的精髓,部分内容也会以动画和代码的形式。后续会覆盖更多人工智能所涉及的数学基础课程:统计,优化等,欢迎大家关注和反馈。
本文对应视频课程第三节中详细解释了6矩阵相乘的5种方法及其理解。
假定 中, A 是 行 列的矩阵, 是 行 列的矩阵, 为 行 列矩阵:
1. B矩阵的列组合:列列切分
这是最经典的理解方式,沿袭了第一部分 的方式。
回顾可以将 视为 的列向量关于每个 分量的线性组合。
那么 相乘可以理解为将矩阵 按列切分成列向量,即
如此,结果矩阵的第 列就是 : 的列向量关于 的线性组合。
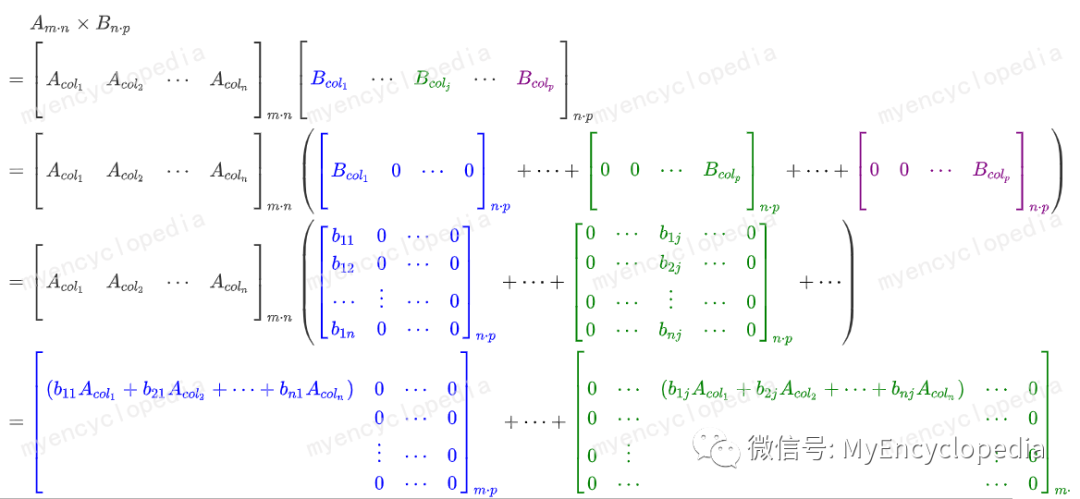
由于我们将 和 都按列来切,这种方式可以助记成 列列 切分。
A矩阵行组合:行行切分
同样的,对应于 右乘向量等同于列的组合, 左乘行向量等同于行的组合:
其结果是一个行向量。
那么 相乘可以理解为将矩阵 按行切分成行向量,即
如此,结果矩阵的第 行就是 : 的行向量关于 的线性组合。
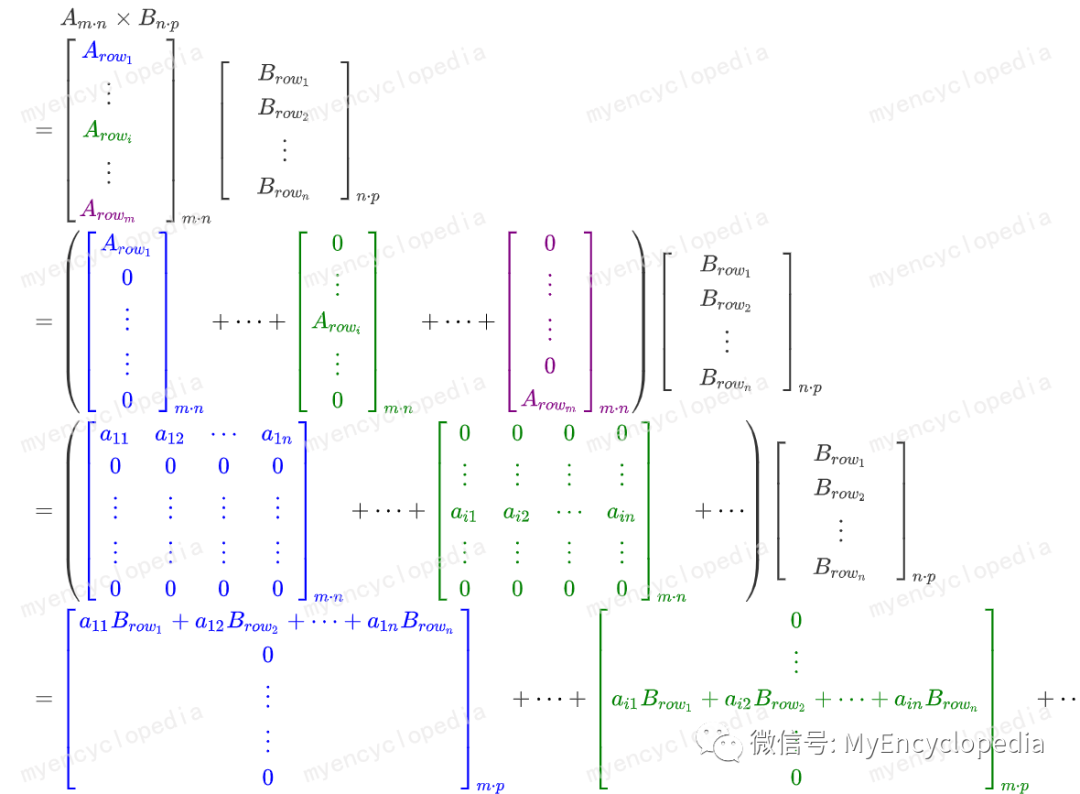
这种方式可以助记成 行行 切分。
A行 x B列 点乘:行列切分
如 矩阵按行切, 矩阵按列切,可住记成 行列 切分,具体推导如下。
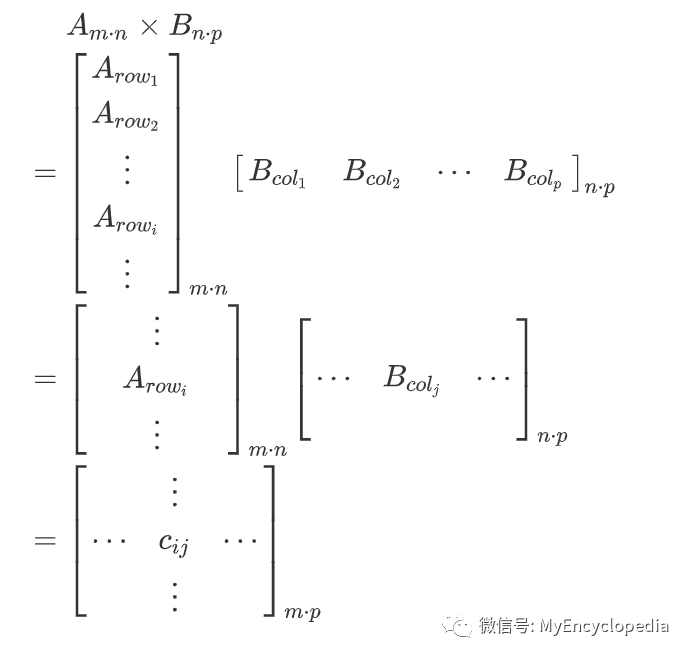
行乘以列即列向量点乘,结果是一个标量。因此 为结果矩阵 的第 行 列的值。
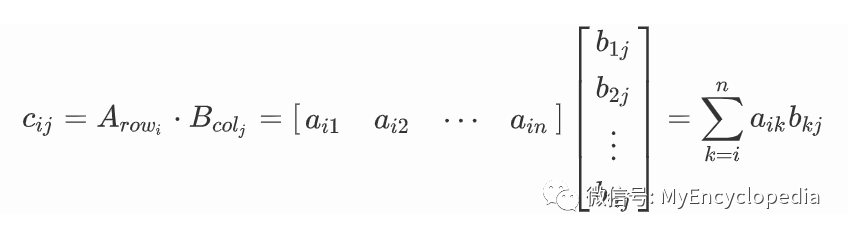
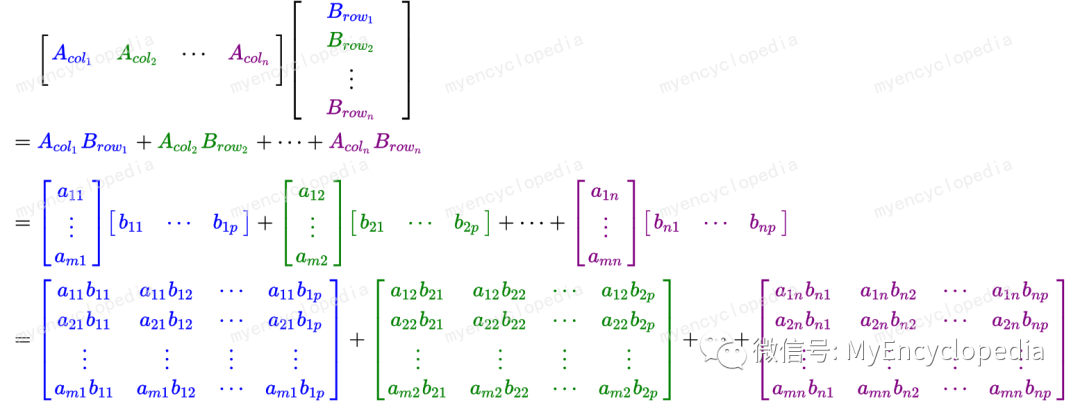
A列 x B行 矩阵和:列行切分
最后,也可也按列行来切分。注意列乘以行时的结果是一个矩阵。
分块相乘
第五种方式是分块相乘,可以认为是点乘理解下的扩展。
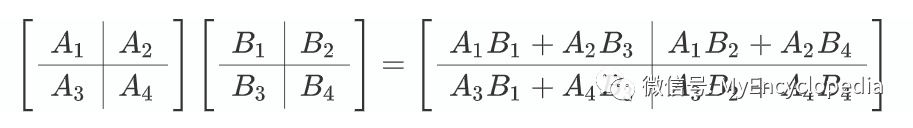
长按扫描下方二维码添加小助手。
可以一起讨论遇到的问题
声明:转载请说明出处
扫描下方二维码关注【集智书童】公众号,获取更多实践项目源码和论文解读,非常期待你我的相遇,让我们以梦为马,砥砺前行!

评论
