两道例题详解贝叶斯定理

导读:本文首先讲解条件概率及贝叶斯定理,之后有两道例题,看看你都能答对吗?

概率在0~1之间变化,即0≤P(A)≤1,其中P(A)代表事件A发生的概率。 如果事件确定发生,则其发生概率为1。即,当事件A确定发生时,P(A)=1。 如果事件确定不会发生,则其发生概率为0。即,当事件A确定不发生时,P(A)=0。 如果事件A和事件B不能同时发生,则称它们是互斥的。当事件A和事件B互斥时,任一事件(事件A或事件B)发生的概率就是每个事件发生概率之和,即:P(A或B)=P(A)+P(B)
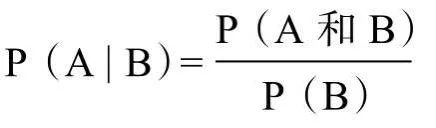
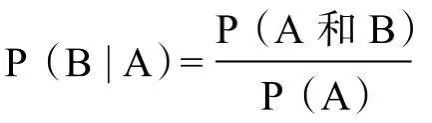
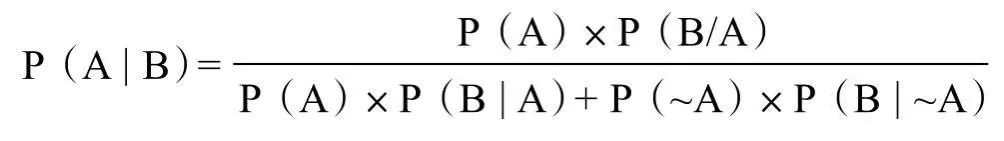
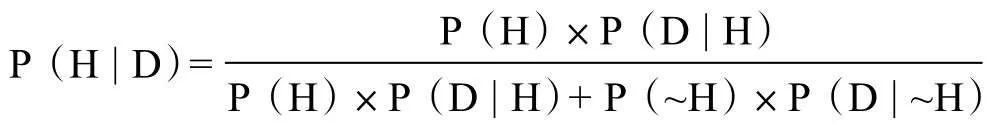
某个夜晚,一辆出租车肇事后逃逸。该城市共有两家出租车公司,一家公司的出租车均为绿色(“绿色”公司),拥有出租车数量为全市出租车总数的85%;另一家公司的出租车均为蓝色(“蓝色”公司),拥有出租车数量为全市出租车总数的15%。一名目击者称肇事出租车是“蓝色”公司的。法院对目击者的证词进行了测试,发现目击者在出事当时那种情况下正确识别两种颜色的概率是80%。那么肇事出租车是蓝色的概率是多少(用百分数表示,范围从0%到100%)?
15%的出租车是蓝色。 目击者认为该出租车是蓝色的(识别准确率为80%)。

假设XYZ病毒能够引起严重的疾病,该病发病率为千分之一。假设有一种化验方法,可以精准地检测到该病毒。也就是说,如果一个人携带XYZ病毒,一定可以被检测出来。但是该项化验的假阳性率为5%,即健康人接受该项化验,会有5%的可能性被误诊为病毒携带者。假设从人群中随机选择一人进行检测,化验结果为阳性(阳性意味着受检者可能是XYZ病毒携带者)。那么,在不考虑具体症状、病史等情况下,此人携带XYZ病毒的概率是多少?(用百分数表示,范围从0到100%。)
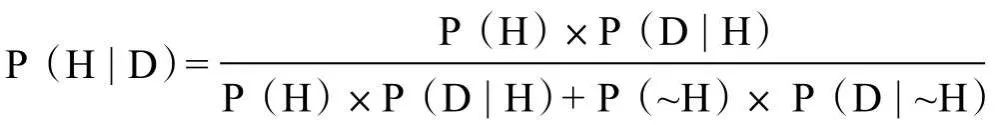
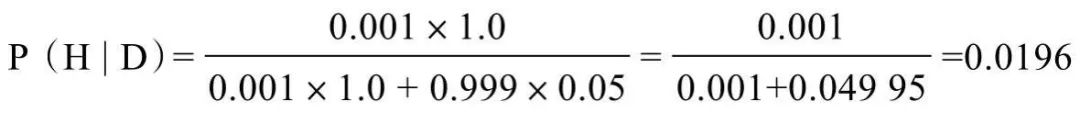

评论
