矩阵之芯 SVD: 基本应用以及与其他分解的关系

上一篇里忘记说了,为什么取名为矩阵之芯呢?
1基本性质
上一篇最后讨论了左右奇异向量具有如下性质,
对于
今天来看看另一个简单但是也挺有用的性质。
令
1、秩
, 等于 的非零奇异值的数量。 2、由左右奇异向量
和
可以构建
验证
注意,最后那个等号对应的式子很有意思,两个矩阵的乘积可以记为两个向量的内积形式。这里,向量都默认写为列向量的形式。
对矩阵乘法的不同理解
上面分解里虽然有三个矩阵,但我们只需要看两个矩阵的乘法。
1、矩阵乘法
从上面式子可以看出来,每个元素都是
2、矩阵乘法
再观察,乘积
所以,将下面这
就是矩阵
§外积展开式
上面性质也可以如下展开,
这里,每一项
2简单应用
这一条简单的性质有什么用呢?
我们知道,
这一点对应的其实就是下面这个低秩矩阵近似问题。
§低秩矩阵近似
一些实际应用需要求解矩阵
其中,对角矩阵
不过这里有个问题,就是这个
那么就选这前
我们将图像灰度看成一个矩阵,然后把它分解了,丢掉一部分重新合成一张图像,看看如何效果。这个例子应该到处都可以看到吧,再来温习一下。
我们来处理一种味道不错的水果(猜猜这是哪个品种)的图像。

import numpy as np
from PIL import Image
import matplotlib.pyplot as plt
plt.style.use('ggplot')
def load(pic):
i = Image.open(pic)
g = i.convert('L')
mat = np.array(g).astype(np.uint8)
return mat
mat = load('orange.png')
plt.figure(figsize=(10, 5))
plt.imshow(mat, cmap='gray')
plt.show()

U, Sigma, V = np.linalg.svd(mat)
U.shape, Sigma.shape, V.shape
((383, 383), (383,), (492, 492))
看看只保留奇异值最大的那个秩 1 矩阵。
k = 1
re_img = U[:, :k] @ np.diag(Sigma[:k]) @ V[:k, :]
plt.figure(figsize=(10, 5))
plt.imshow(re_img, cmap='gray');
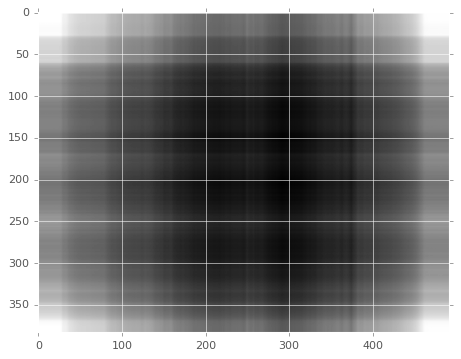
灰蒙蒙一片啊,那就再多看几个。下面我们来按照百分比来自动计算这个
def select_k(sigma, pcent):
s = np.add.accumulate(sigma)
s = s/s[-1]
return np.where((s>=pcent)==True)[0][0]
select_k(Sigma, 0.9)
85
前 85 个奇异值就占了百分之九十的信息量。
# 查看前百分之 70、80、90、100 的重建效果
for i in [select_k(Sigma, 0.7), select_k(Sigma, 0.8), select_k(Sigma, 0.9), select_k(Sigma, 1.0)]:
re_img = U[:, :i] @ np.diag(Sigma[:i]) @ V[:i, :]
plt.figure(figsize=(10, 5))
plt.imshow(re_img, cmap='gray')
title = "n = %s" % i
plt.title(title)
plt.show()



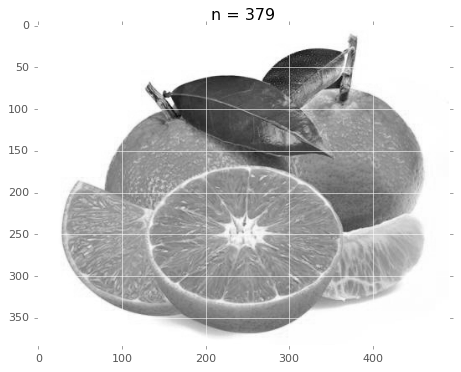
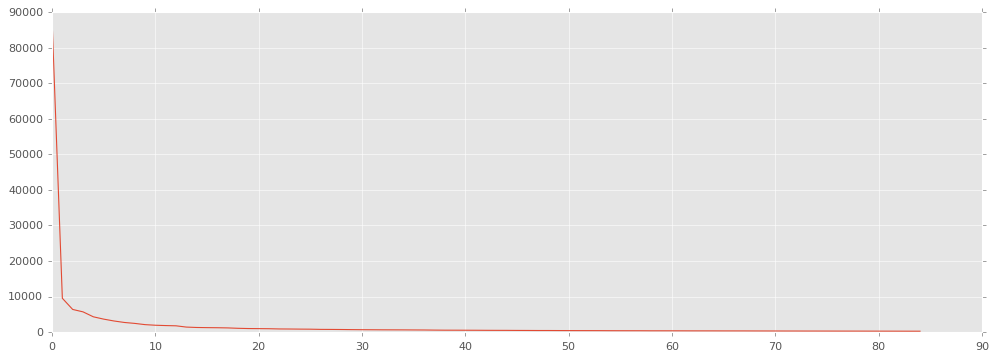
有没有发现,用 85 个秩 1 矩阵生成的结果跟原图差别不大吧。把前 85 个奇异值画出来看看。
plt.figure(figsize=(15, 5))
plt.plot(Sigma[:85]);
3与其他分解的关系
§与特征分解的关系
从可以应用于任何
给定
上面等式的右边是左边的特征分解。具体来说,
的列(右奇异向量)是 的特征向量。 的列(左奇异矢量)是 的特征向量。 的非零元素(非零奇异值)是 或 的非零特征值的平方根。
正规矩阵
正规矩阵定义: 对于复数值方阵
其中,
而下面分解
也被称为矩阵的酉对角化。
如果
如果
在实数域内,如果
根据谱定理可知该类矩阵可以使用特征向量对它进行对角化,因此可以将其写为
当
实对称矩阵
作为一种更特殊的情况,对于每个
其中,
其展开式跟 SVD 分解也有类似形式,
一般矩阵的特征分解
除了半正定正规矩阵外,
特征分解为
另外,只有具有完备特征向量集的方阵具有特征分解,但是任何
例子
给定如下实矩阵,
可以求得对
即有,
§一般矩阵
SVD 与不能作特征分解的更一般的矩阵之间的联系则可以通过极分解来建立,例如在实数域,可以构建如下分解
