矩阵之芯 SVD - 从奇异值角度看矩阵范数
首先,我们回顾一下矩阵奇异值分解的基本性质。
令
1、如果
,即矩阵 的秩为 ,那么 的非零奇异值的数量等于 。 2、将两个正交矩阵分别看成按左、右奇异向量按列排列,即
以及
则
1矩阵范数
在上面这篇里,我们介绍了向量的范数,那么矩阵的范数又是怎么样的呢?
.定义
考虑实数域上的矩阵,范数是满足以下性质的从
,以及 对于任意数
,有 对于可相乘矩阵,有
.矩阵 F-范数
矩阵
我们知道,矩阵具有专门的乘法,从而将它与一般的向量空间区分开。但是向量范数的三个性质与向量乘积并没有关系。
因此,对于矩阵来说,貌似需要一个额外的性质,能够将
而 F-范数刚好具有此额外性质,即
因此有,
可以说 Frobenius 矩阵范数
相容性条件
简写为,
因此可将乘积性质
除了 Frobenius 范数满足前面矩阵范数的定义外,但是其他有用的矩阵范数又是从何而来呢?
实际上,如下所述,每个合法的向量范数都会生成(或诱导出)一个矩阵范数。
.诱导矩阵范数
在
连续函数在有界闭区域上必有最小、最大值。
很明显,在某种意义上,诱导矩阵范数与其基础向量范数相容,即
当 非奇异时,
证明
容易验证
换句话说,诱导范数
下图描述了在
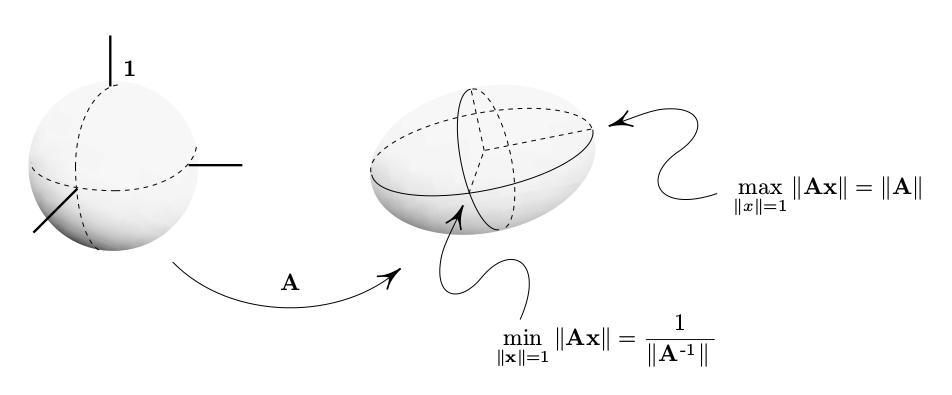
2奇异值与矩阵范数
下面,我们从奇异值角度审视一下矩阵的几个常用范数。
我们再次来看一下矩阵的秩 1 展开式,
注意看,上面将矩阵
由上面诱导矩阵范数的定义可知,范数在一定意义上是考量一个矩阵对单位向量的缩放能力。我们将展开式代入矩阵向量乘积,
矩阵对单位向量的变换可以按奇异值和相应的奇异向量分解开,而缩放能力主要反映在奇异值上。
那么,我们能不能直接从奇异值来考量或定义矩阵范数呢?
.Schatten p-范数
由矩阵
定义如下范数,
巧的是,这样用向量范数直接从奇异值定义的矩阵范数与常规方式定义的矩阵范数之间真的有等价关系。不信请看:
1、矩阵
其中,
2、矩阵
3、矩阵
定义如下,
也称为矩阵
下面我们来对上面的定义简单地解读一番。
由
令
因此,
.程序小实验
import numpy as np
from scipy.linalg import sqrtm
A = np.array([[1,2,3],[1,1,1],[0,1,-1]])
A
array([[ 1, 2, 3],
[ 1, 1, 1],
[ 0, 1, -1]])
U, S, V = np.linalg.svd(A)
AtA = A.T@A
AtA
array([[ 2, 3, 4],
[ 3, 6, 6],
[ 4, 6, 11]])
m = np.diag(S)@V
m
array([[-1.31467133, -2.16665828, -3.20525993],
[ 0.19957118, 1.13213211, -0.84714312],
[ 0.48146718, -0.15449536, -0.0930447 ]])
root_VSVT = V.T@np.diag(S)@V
root_VSVT
array([[0.90174674, 0.71064345, 0.82573525],
[0.71064345, 2.09285003, 1.05591886],
[0.82573525, 1.05591886, 3.03367709]])
S.sum()
6.028273858670582
root = sqrtm(AtA)
root
array([[0.90174674, 0.71064345, 0.82573525],
[0.71064345, 2.09285003, 1.05591886],
[0.82573525, 1.05591886, 3.03367709]])
root@root
array([[ 2., 3., 4.],
[ 3., 6., 6.],
[ 4., 6., 11.]])
np.trace(root)
6.028273858670583
3小结
将
矩阵对单位向量的变换可以按奇异值和相应的奇异向量分解开,而缩放能力主要反映在奇异值上。
因此,我们可以从奇异值的大小(甚至数量)来定义矩阵范数。可见,奇异值的确很厉害吧。
