原来激活函数是这样基活神经网络的
如何比较数学地诠释格局比努力更重要。
01坐标系的选择
数学中一个基本但又重要的方法是找到一个坐标变换,让复杂甚至不可能问题变得简单可行。
举个栗子,就是一个圆的方程。如果是在笛卡尔坐标系下用方程表示单位圆的话,可以将圆的轨迹表示为如下隐函数,

但是,如果将 y 求解出来,以获得显式表达式的话,情况将会变得很糟,
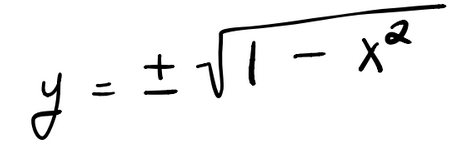
这样做,我们必须将平方根的两个分支(圆的上半部分和下半部分)对应的简单函数组合在一起才能表示一个完整的圆。这种表示方式不仅美学上有所遗憾,还有碍于展示圆固有的几何简单性。
讲到这里,想到一个疑问。圆的轨迹貌似需要两个坐标来刻画,但是古人(不管中国人还是外国人)还没有坐标的概念,那么古代数学家是如何描述圆的呢?
A circle is a plane figure bounded by one curved line, and such that all straight lines drawn from a certain point within it to the bounding line, are equal. The bounding line is called its circumference and the point, its centre.
“圆,一中同长也”。
这就是墨家经典《墨经》中对圆下的定义。

墨子虽然以思想家传世,但其实是木匠出身。不过,跟一般木匠不同,干技术活的同时还喜欢钻研光学、力学和几何学等。估计是靠画线、画圆、打孔等技能吃饭的同时启发了他对相关问题的思考,从而提出了一些概念和方法。
比如讲计算机视觉时不得不提的一项我国古代的创举,小孔成像,就是他老人家及门徒的杰作。这可能也是第一颗量子科学实验卫星取名墨子号的原因吧。
再进一步,如果要定义椭圆呢?我国古代貌似没有椭圆的概念,但顺着墨家定义圆的方式,可以推广一下。那应该就是: 椭圆,两中同长也。
在那个没有坐标系,没有符号的年代,墨家学派提出了很多数学中的概念。不过,他们也没有提出坐标系这个强大的数学工具。但如果在他们定义圆的时候配上一个坐标系,那我想应该是极坐标。
现在我们知道了,因为古代没有坐标系,所以不能用公式来表示图形。只能用文字来描述,古希腊人的定义虽然很详细,但跟墨家的定义在意思上完全一致。
不过要注意的是,坐标系只是工具,能用它来更好地解决某些问题。但并不代表没有它不行,甚至数学家后来又会追求不依赖于坐标系的办法。

事物及其性质以及事物之间的关系等,本身就在那里,不需要坐标系。只是便于我们刻画,所以才引入不同的坐标系。如果把坐标系比作衣服,那么有些衣服可能会更合身,但是不穿衣服也有不穿衣服的美。
绕了一大圈想说什么呢?其实想说的是,对于像圆这种图形,直角坐标并不直观(我们现代人的脑袋已经从小被数学知识改造过了)。也许另一个坐标更自然,对,那就是极坐标,用(距离,角度)来表示,而不是两个抽象的变量。
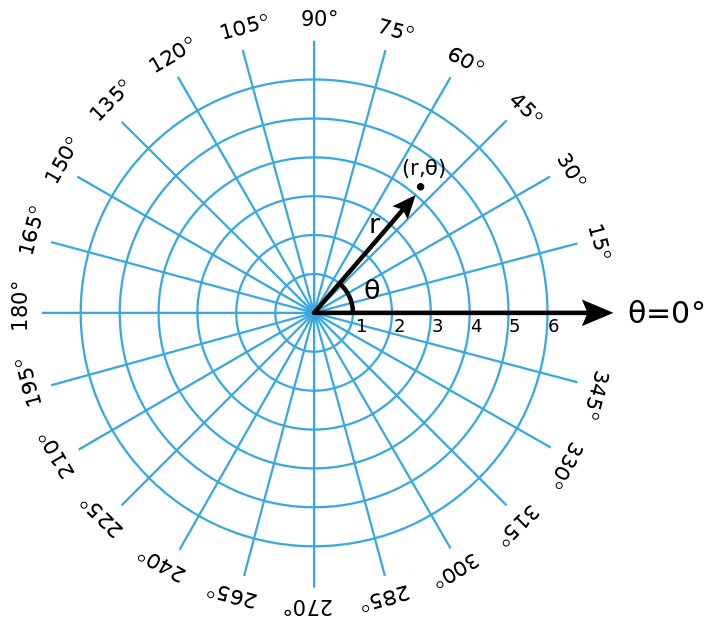
如果我们使用极坐标表示单位圆,它将变得简单明了。
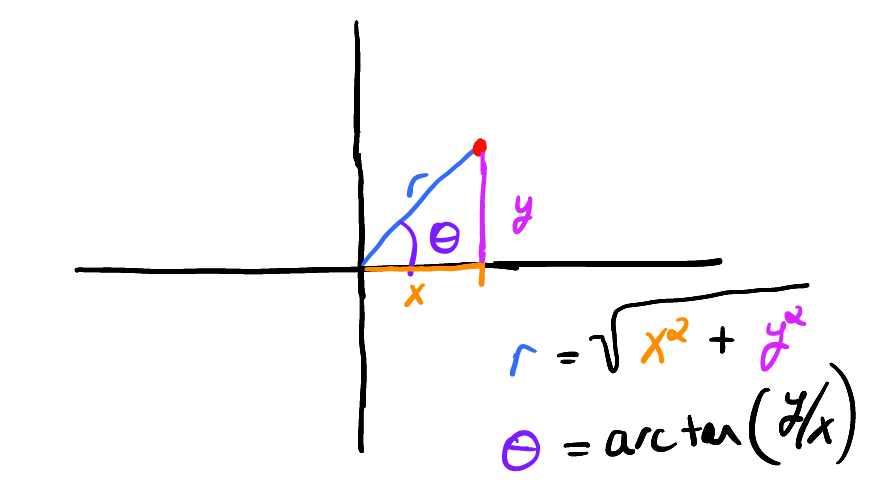
在极坐标中,我们的单位圆采用简单形式
直角坐标是矩形的自然坐标,极坐标是圆形的自然坐标。本文将把这种思路简单应用于构建神经网络,通过一个示例来说明选择正确坐标系的重要性。
02神经网络拟合函数
我们知道,人工神经网络(ANN)就是通过将简单的非线性函数(层)链接起来构建的网络(函数)。
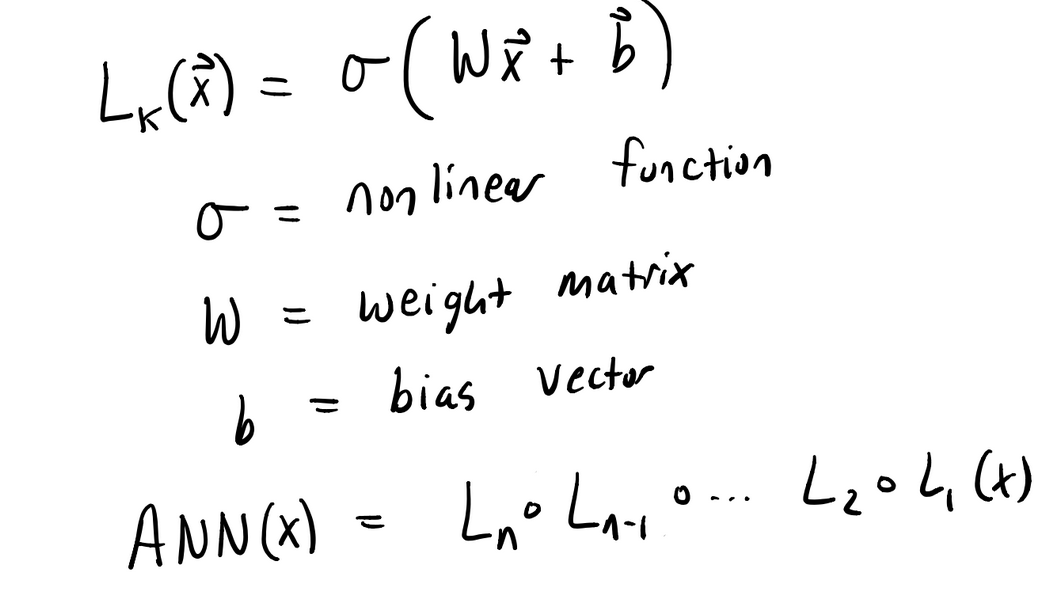
万能逼近定理告诉我们,通过将这些简单层链接在一起,我们可以用有限深度和宽度的 ANN 来逼近表示一般的函数。不严谨地说,激活函数的多重复合构成了神经网络的坐标系。不同的坐标系可以让神经网络具有不同的格局或者世界观。
让我们看一个简单的例子,看看如何使用神经网络来近似逼近正弦函数。
03神经网络拟合 sin(x)
让我们应用这种功能强大的函数逼近方法来构建简单函数
下面的代码使用标准的非线性函数 tanh 构建一个具有两个隐藏层的简单网络。
ann = Chain(Dense(1,20,tanh),Dense(20,20,tanh),Dense(20,1));
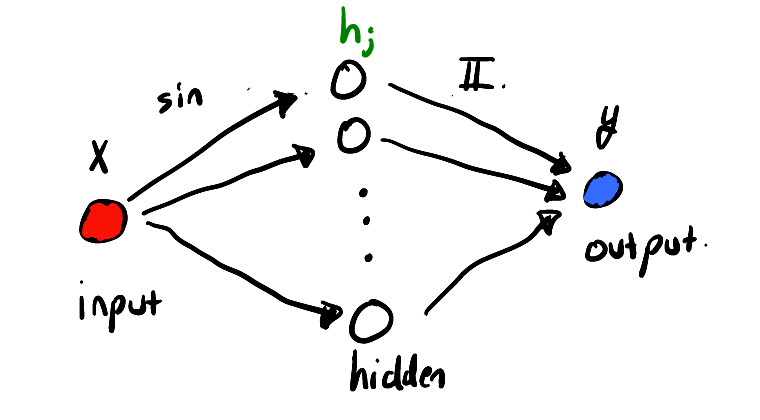
来个草图展示一下该神经网络,
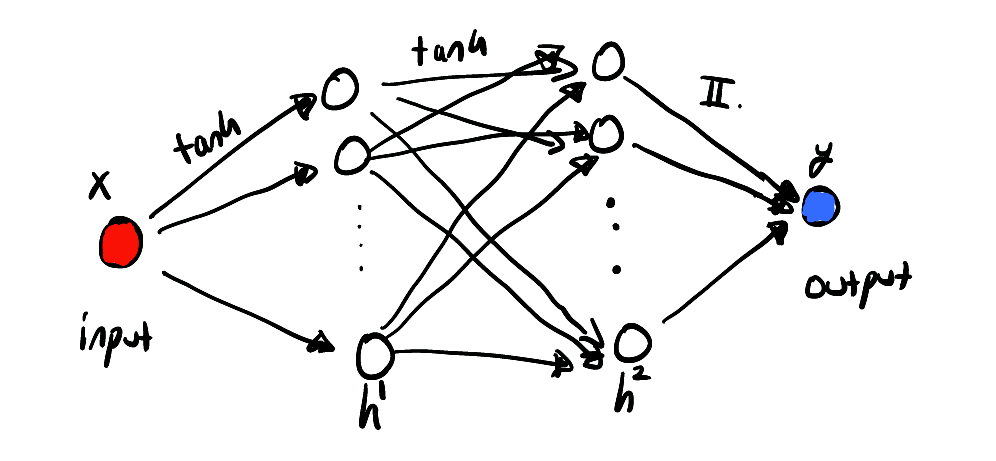
上图显示了我们只有一个输入和输出值,中间有两个隐藏图层。可以这么理解,该网络用于表示特定的一个函数族,通过固定参数来指定其中的一个具体函数。
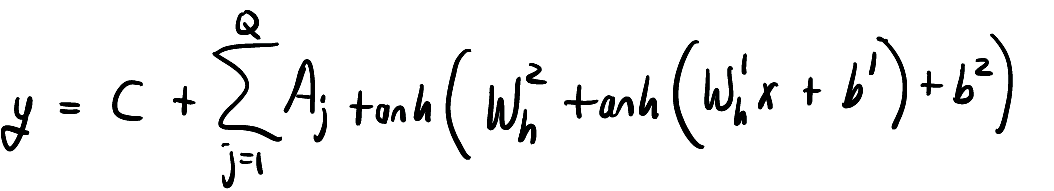
好了,我们希望可以用该函数族中的某个成员来近似表示函数
但是我们没有这般神力,即使拿出纸和笔去演算也很难下手。那怎么办呢?我们可以用数据驱动的方法来处理。为了尝试找到最接近它的成员,我们可以使用一些训练数据通过最小化误差来找到那些参数。
function loss(x, y)
pred=ann(x)
loss=Flux.mse(ann(x), y)
#loss+=0.1*sum(l1,params(ann)) #l1 reg
return loss
end
@epochs 3000 Flux.train!(loss,params(ann), data, ADAM())
拟合神经网络后,我们可以看看它对训练数据和一组测试数据的表现如何。
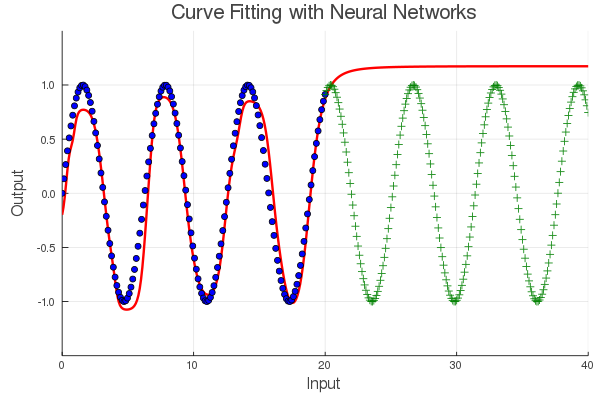
这个神经网络好像学会了一部分,但其他部分就错的离谱了,怎么回事呢?这其实跟我们的目标有关系,我们要表示的正弦函数是个周期函数,但是我们的数据只有部分。换句话说,从这些数据中学不到周期性,因此网络并没有捕获信号的周期性,用行话说就是对测试数据的泛化极差(绿色)。
这是什么地方出错了呢?经常被引用的万有逼近定理告诉我们,可以使用有限深度和宽度的前馈神经网络来表示一般的函数。对的,神经网络存在某些参数(权重和偏置)可以用来表示函数,这点没错,但它并不意味着我们可以轻松地找到这些参数。
好吧,那我们再次尝试应用蛮力来建立更深的网络或训练更长的时间呢。但是,别急,让我们改变一下思路。一个非常简单的更改将使我们在很短的时间内得到一个接近完美的近似值。
Ξ巧妙的做法
有了这些数据,我们可以看到它是周期性的。但是,我们前面的神经网络根本没有考虑这层信息。那怎么利用周期性呢?除了使用 tanh 非线性函数外,我们也可以使用 sin 函数啊。这样,我们第一层的输出将是周期性的。
对啊,激活函数不一定就是 tanh 和 sigmoid 之类的函数,也可以是个周期函数啊,比如 sin 函数。这样一整,我们的神经网络将具有天生的周期预见性。所谓的激活函数,相当于赋予了神经网络一定的世界观。
下图显示的是为该系统提供更好的近似网络的想法。
我们用函数形式写出上面使用的网络,

其中 Q 是隐藏层中神经元的数量。这在 Flux 中很容易做到,
Q = 20;
ann = Chain(Dense(1,Q,sin),Dense(Q,1));
让我们来拟合这个新模型,看看是否可以获得更好的效果。
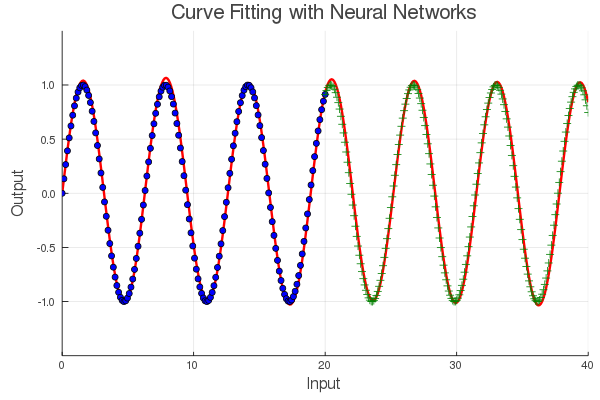
是不是如有神力,一下让神经网络开了天眼的赶脚?显然,这是一个更好的模型,因为它捕获了周期性。但是,请注意,我们在训练和测试数据上仍然略有偏差。这可能是因为我们的模型仍然具有实际上并不需要的额外自由度。
我们可以通过对参数应用一些正则化来解决此问题,但是针对这个例子,我们可以用非常酷的数学来改善它。

其实呢,上面的神经网络的功能形式与傅立叶级数的形式非常接近。傅立叶级数是一组基,可用于表示有限域 [a,b] 上所有的好函数。如果函数是周期性的,则可以将对有限域的描述扩展到整个实数轴。因此,傅立叶级数通常用于周期函数。
傅立叶级数的形式为,
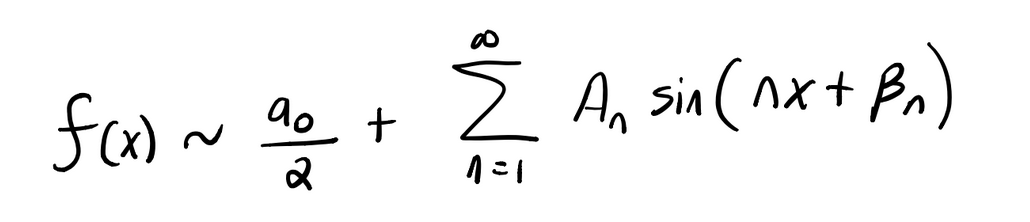
我们的神经网络与傅立叶级数之间的唯一区别是我们的神经网络允许权重
在 Flux 库中,很容易从可训练的参数集中删除第一层中的那些权重参数。通过将它们设置为整数值,我们实际上可以创建一个神经网络,它是一个傅立叶级数。
# Fourier Series ANN
Q = 20;
ann = Chain(Dense(1,Q,sin),Dense(Q,1));
function loss(x, y)
pred=ann(x)
loss=Flux.mse(ann(x), y)
return loss
end
opt = ADAM()
ps=params(ann)
for j=1:20
ann[1].W[j]=j
end
delete!(ps, ann[1].W) #Make the first layers weights fixed
@epochs 3000 Flux.train!(loss,ps, data, opt)
下图展示的是使用傅立叶 ANN 拟合 sin(x) 函数的效果,
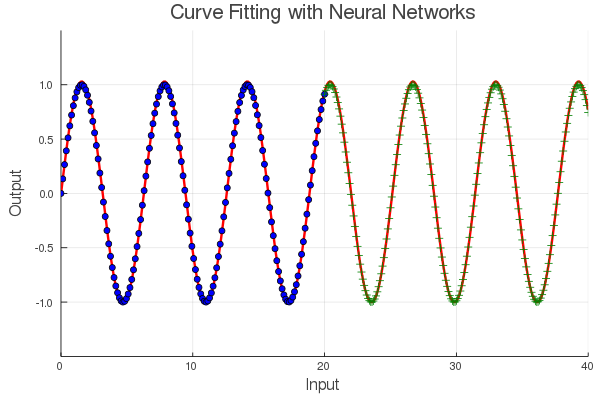
如果你想知道这种方法是否可以很好地泛化到其他更复杂的周期函数。考虑一个混有一些高次谐波的周期信号。
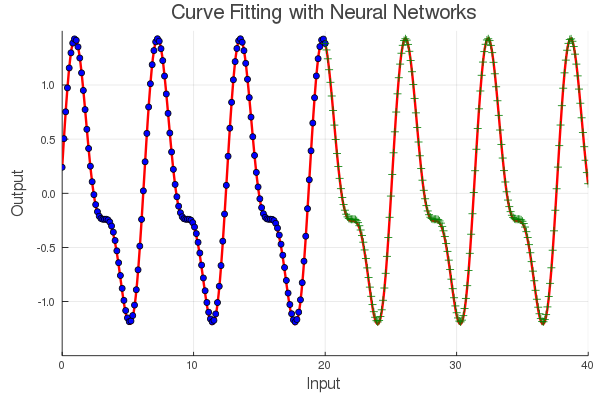
04小结
这个简单的示例提供了一些有关 ANN 的工作原理以及我们如何改进模型的重要见解。神经网络的设计会对结果产生巨大影响。对问题和领域的特定了解会产生巨大的影响。 确保将你所知道的有关问题的所有信息都传达给神经网络。在这里,我们看到告诉函数产生周期性信号的作用远远超过了增加网络规模或训练时间所能带来的好处。
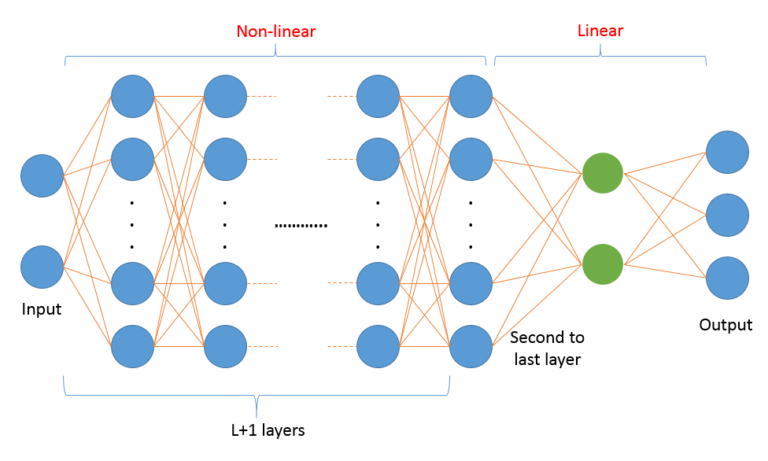
Ξ划重点
神经网络相当于定义了一个函数空间,空间的坐标系(基)是通过一系列网络层以及激活函数以多重复合方式构建出来的。 构建神经网络时用到的激活函数在表示这个函数空间的坐标系(基)上发挥了重要作用,不同的激活函数能让网络具有不同的表达能力,具体设计就看具体问题。 有时候,给网络配上合适的坐标系,会事半功倍,比加深网络、努力训练更重要。这叫什么来着?有没有那么点格局比努力更重要的赶脚?
⟳参考资料⟲
Flux: https://github.com/FluxML/Flux.jl
[2]Kevin Hannay: https://towardsdatascience.com/work-smarter-not-harder-when-building-neural-networks-6f4aa7c5ee61
[3]code: https://github.com/khannay/CurveFittingNeuralNets
