随机梯度蒙特卡洛算法-重要性采样|NeurIPS 2020

极市导读
重要性采样是蒙特卡洛方法中的一个重要策略。该方法不改变统计量,只改变概率分布,可以用来降低方差。本文作者通过通俗易懂的动图描述算法,阐述了发表在NeurlPS2020上一篇关于重要性采样的文章。>>加入极市CV技术交流群,走在计算机视觉的最前沿
大家好,在此宣传一篇NeurIPS 2020文章。为了少占用大家时间,我会用通俗的动图描述算法,抛砖引玉。文章的理论性质和潜力值得让数学大神加以改进并被计算机大牛发扬光大。
A Contour Stochastic Gradient Langevin Dynamics Algorithm for Simulations of Multi-modal Distributionsarxiv.org
文章地址:https://arxiv.org/pdf/2010.09800.pdf
话不多说,先放一个模拟图,一个分布有9个mode,中间一个概率最大,边上次之,角上四个最小。如果你能准确采样分布,你就能获得正确的预测分布。这在避免第二类统计错误(把不对的归为是对的)和增强学习中有巨大前景。深度学习中一个标准的采样算法是随机梯度朗之万动力学(SGLD),如图所示,粒子会在坑中逗留很久,坑越深,逗留时间指数变长。也就是说,采样这个分布是极其慢的。
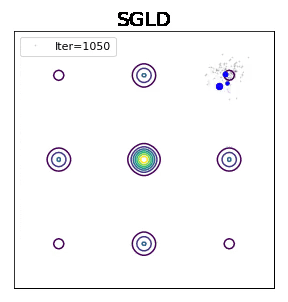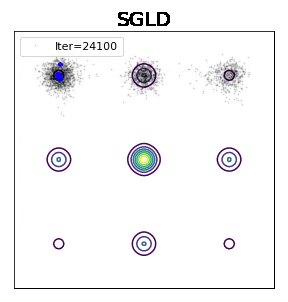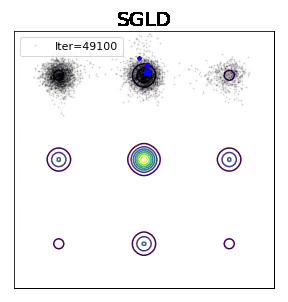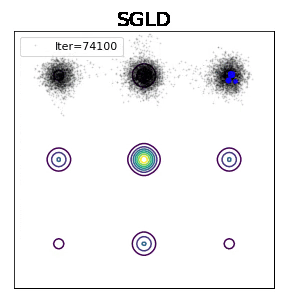
Welling and Teh - ICML 2011
有研究者尝试过一个简单的idea,即采用周期性cosine学习率获得不错的实验表现。大学习率explore新区域,小学习率获得局部采样。图下可见,效果比SGLD提升了一些。
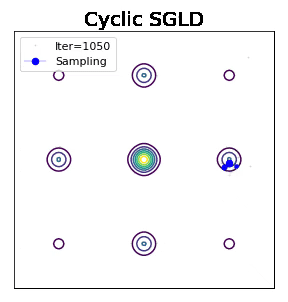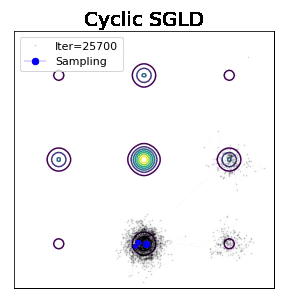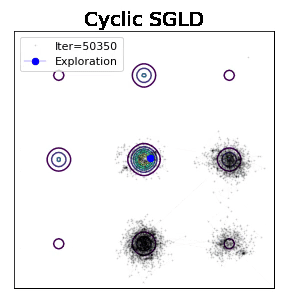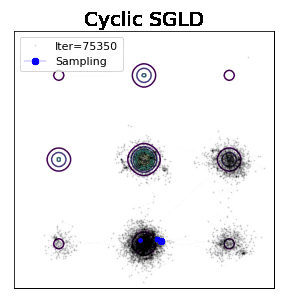
Zhang - ICLR 2020
当然,@Zhanxing Zhu老师的变温tempering算法,对non-convex问题也很有潜力。对于preconditioned SGLD@Chunyuan Li,它对Hessian条件数糟糕的情况做了一定的改进。
更著名的算法是经典的并行回火(Parallel tempering/ replica exchange)算法。思想是引入两个(或多个)随机过程,高温过程探索全局(exploration),低温过程采样(exploitation)。当高温过程能量(loss)值比低温过程没差很多时,参数有一定概率去互换(swap)。利用跳跃(jump)的方式解决爬坡难的问题。
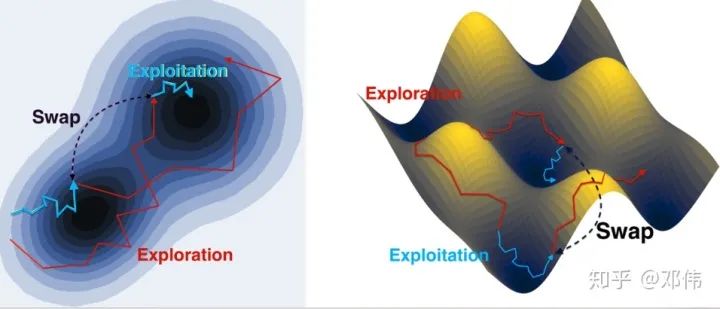
由于逃脱local trap需要的代价是指数级别(和深度有关),因此这个算法用较小代价获得了指数加速。此算法如此流行且重要甚至都出现在阿里数学竞赛试题里(忘了哪一版了)。
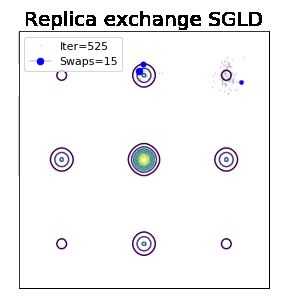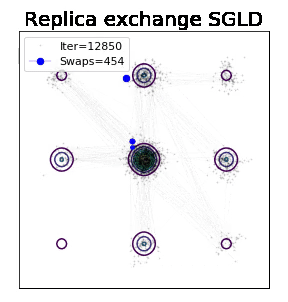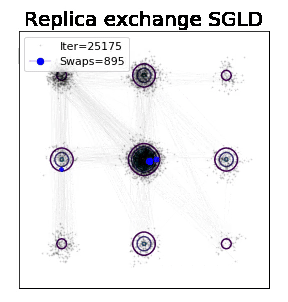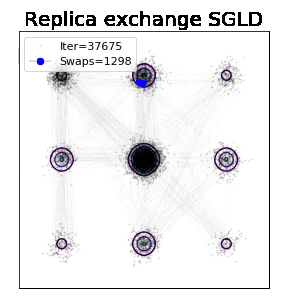
直观想象,如何跨越能量壁垒是加速采样的重中之中。而现实下,鱼和熊掌不可得兼,exploration and exploitation常常只能取舍。多个过程/引入跳跃无疑会很好的克服这一问题。但如果只用一个过程不带跳如何达到理论上最大的潜能呢?传统MCMC领域公认的一个答案是:重要性采样(importance sampling):
即如果 分布很难采样,但 分布容易的多,同时你还能获得分布之间的关系 (Radon nikodym导数,importance weight)。那么你可以通过间接采样来大大加速 的模拟。
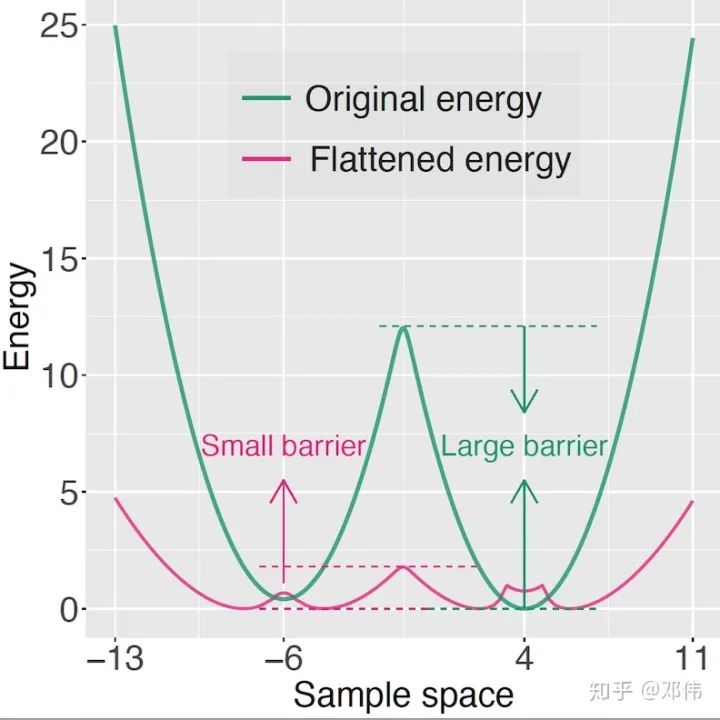
什么样的分布比分布容易采样呢?Neal在Annealed Importance Sampling提出用高温的思路将分布变平。这篇文章采用的则是统计物理里面的multicanonical ensemble和Wang-Landau里面的思路,将原分布(下图绿线)除以目标分布的能量pdf(也将作为importance weight)来将分布变平(下图红线)。
从而降低能量壁垒。该思想已经在统计物理和生物信息学领域获得极大成功,被王永雄、刘军教授(两位COPSS奖:统计菲奖,一年一人,coadvisor的老板和师兄)评价为最适合加速蒙特卡洛的算法。
尽管目标分布的能量pdf刚开始不知道,但获得能量pdf比获得分布信息要容易的多(比如一个Gaussian mixture with equal weight, 估计单个mode的能量pdf很容易,而这个信息已经足够;进一步的话,不equall weight也不是啥问题)。我们可以用stochastic approximation(可以想象成EM算法的进阶版)一边采样一边优化隐变量。均衡情况下,隐变量收敛到能量pdf,目标参数弱收敛到更容易采样的 分布。神奇的是,此算法拥有简洁的形式(比原算法只多了下面一行迭代,相比之下Adam需要额外5层迭代)
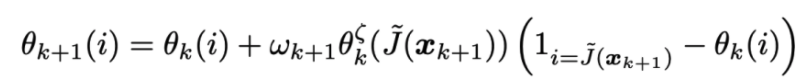
和极佳的稳定性,隐变量可以收敛到唯一fixed point而无关凸性(EM算法常见问题就是隐变量local trap且极其不稳定)。该算法和拟牛顿算法有一丝相似。但拟牛顿不改进能量函数只是估计Hessian,因此只能获得渐进超线性的表现;而我们的算法步步改变几何形状的做法,潜在的指数加速了收敛(为啥指数阶的话,由于分析很难,我还是引一篇reference吧)。
参考文章:https://arxiv.org/pdf/1501.07094.pdf
下面是路径展示:此算法引入一个隐变量,这个隐变量代表分布的能量pdf,原始分布除以这个隐变量可以获得更平的分布因而更容易模拟,你能看出高能区似乎也有很多样本,由于他们对应的importance weight很小,因此结合importance weight 还是可以恢复原始分布。能量pdf刚开始未知,但是一些初步的学习后便可以获得巨大的加速效果。
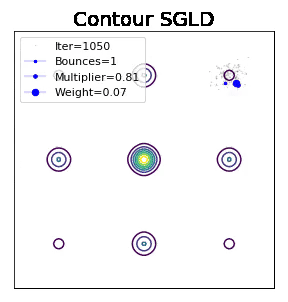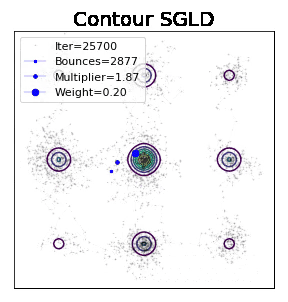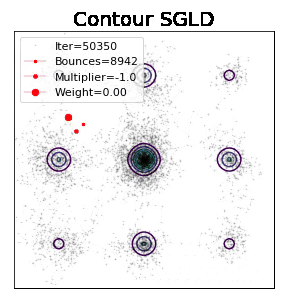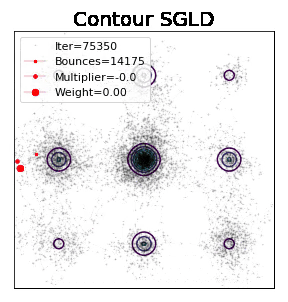
这份工作是统计物理里面Wang-Landau算法从Metropolis kernel 到Langevin kenel的拓展,为一类重要的加速技巧adaptive biasing force做了铺垫。为了能应用在深度学习领域,我们顺便把随机梯度的版本也一并做了出来。simulation比肩甚至超越parallel temerping的性能证明了其巨大的潜能。
此文章最大的novelty在于methodology development。如果你看到simulation的潜能不觉得新奇就可以无视后续了。虽然提供了一些简单的DNN实验,但实验中高loss下,概率分布的估计会变得困难,比如 在数值难估计。折中的办法有很多,就不在此文一一探讨了。应用的工作留给更专业的同学进行了。
改变几何形状带来的理论增益远超Hessian估计,动量,或者高阶数值格式。但也需要更高阶的数学技巧(大量PDE和黎曼几何袭来)。既有挑战性,也有无限潜力。呼唤真 数学大神关注此问题。
1. Max Welling, Yee Whye Teh. Bayesian Learning via Stochastic Gradient Langevin Dynamics. ICML'11
2. R. Zhang, C. Li, J. Zhang, C. Chen, A. Wilson. Cyclical Stochastic Gradient MCMC for Bayesian Deep Learning. ICLR'20
3. W. Deng, Q. Feng, L. Gao, F. Liang, G. Lin. Non-convex Learning via Replica Exchange Stochastic Gradient MCMC. ICML'20.
4. W. Deng, G. Lin, F. Liang. A Contour Stochastic Gradient Langevin Dynamics Algorithm for Simulations of Multi-modal Distributions. NeurIPS'20.
推荐阅读

