【论文解读】GCN论文阅读总结
本次要总结的论文是 Convolutional Neural Networks on Graphs with Fast Localized Spectral Filtering,论文链接GCN[1],参考的代码实现GCN-code[2]。
不得不说,读懂这篇论文难度较大,因为里面有许多数学推导,要了解较多的数学知识。本人数学一般,因此在读本论文的同时参考了网上部分较优秀的讲解,这里会结合我对论文的理解,对本论文下总结,文末会详细列出我参考的讲解链接。
「建议在非深色主题下阅读本文,pc端阅读点击文末左下角“原文链接”,体验更佳」
回顾卷积定义与CNN
传统傅里叶变换与卷积
拉普拉斯算子与拉普拉斯矩阵
GCN模型
切比雪夫多项式及其捕捉局部特征
Graph Coarsening(图粗化)
文本分类实验(Text Categorization on 20NEWS)
数据预处理步骤
模型部分
实验结果
个人总结
参考文献
回顾卷积定义与CNN
我们知道卷积神经网络(cnn)在图像、视频、语音识别等领域取得了巨大的成功。cnn的一个核心内容就是卷积操作。
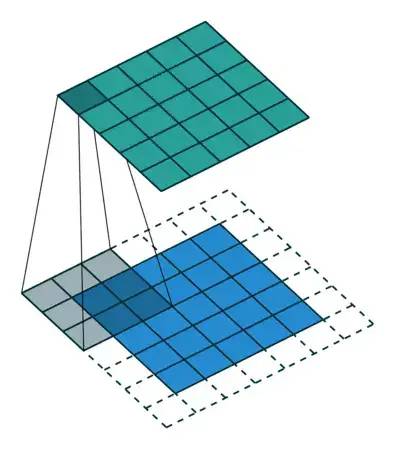
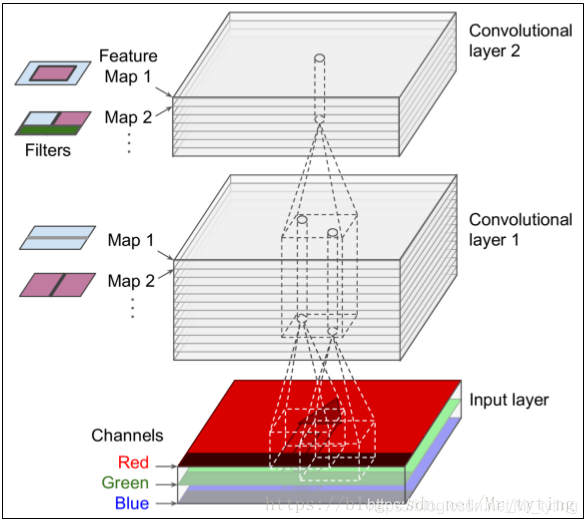 卷积核:上图中的feature map
参数共享机制:假设每个神经元连接数据窗口的权重是固定的
卷积核:上图中的feature map
参数共享机制:假设每个神经元连接数据窗口的权重是固定的
❝对于input layer中,不同的数据区域,卷积核参数是共享的,但是不同的输入通道卷积核参数可以不同
❞
这种参数共享机制有如下两个优点
大大减少了模型需要学习的参数 可以将卷积操作理解为 平移不变的滤波器,这意味着它们能够独立于其空间位置识别相同的特征。
在维基百科里,可以得到卷积操作的定义: 为 的卷积
连续形式
离散形式
❝更深入的理解可参考知乎这个回答:如何通俗易懂地解释卷积?[3]
❞
那么对于「不规则或非欧几里德域上」的结构数据,例如社交网络用户数据、生物调控网络上的基因数据、电信网络上的日志数据或单词嵌入的文本文档数据等,可以用图形(graph)来构造,cnn上的卷积操作想直接推广到graph上并不是简单可行的,「因为卷积核池化操作只能作用在规则的网格中。」

由上面一张社交网络图可以看出,每个顶点的邻居顶点数量可能都不一致,无法直接使用卷积核池化操作进行特征提取。
为此还需要了解傅里叶变换以及拉普拉斯算子。
传统傅里叶变换与卷积
傅里叶变换的核心是「从时域到频域的变换,而这种变换是通过一组特殊的正交基来实现的。即把任意一个函数表示成了若干个正交函数(由sin,cos 构成)的线性组合。」
Fourier变换
❝为傅里叶变换基函数,且为拉普拉斯算子的特征函数
❞
Fourier逆变换
定义 是 和 的卷积,则有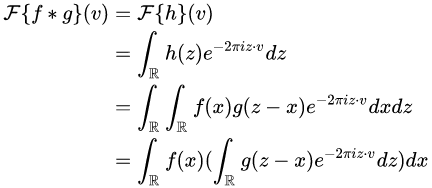 代入
代入  最后对等式的两边同时作用 ,得到
最后对等式的两边同时作用 ,得到 也即是:「即对于函数 与 两者的卷积是其函数傅立叶变换乘积的逆变换」
也即是:「即对于函数 与 两者的卷积是其函数傅立叶变换乘积的逆变换」
即可以通过傅里叶变换得到函数卷积结果。
那么问题来了,如何类比到graph上的傅里叶变换呢?
拉普拉斯算子与拉普拉斯矩阵
这里只说几点重要的结论
拉普拉斯算子计算了周围点与中心点的梯度差。当 受到扰动之后,其可能变为相邻的 之一,「拉普拉斯算子得到的是对该点进行微小扰动后可能获得的总增益」 (或者说是总变化)。 「拉普拉斯矩阵就是图上的拉普拉斯算子,或者说是离散的拉普拉斯算子」;拉普拉斯矩阵中的第 行实际上反应了第 个节点在对其他所有节点产生扰动时所产生的增益累积。直观上来讲,图拉普拉斯反映了当我们在节点 上施加一个势,这个势以哪个方向能够多顺畅的流向其他节点。「谱聚类中的拉普拉斯矩阵可以理解为是对图的一种矩阵表示形式。」
❝拉普拉斯矩阵实际上是对图的一种矩阵表示形式,这句话太重要了 更深入的证明请查看拉普拉斯矩阵与拉普拉斯算子的关系[4]
❞
上面讲到传统的傅里叶变换:
其中 为拉普拉斯算子的特征函数:
类比到图上,拉普拉斯算子可以由拉普拉斯矩阵 代替。而由于 为半正定对称矩阵,有如下三个性质:
实对称矩阵一定n个线性无关的特征向量 ,且 半正定矩阵的特征值一定非负 实对阵矩阵的特征向量总是可以化成两两相互正交的正交矩阵
其中 为特征向量, 为特征值构成的对角矩阵。
那么 在图上的傅里叶变换可以表示如下:
其中 表示第 个特征, 表示graph上顶点个数。
❝可以看出等式左边是以特征值为自变量,等式右边以顶点为自变量,同样可以类别理解为从一个域转换到另外一个域
❞
表示图 上的顶点数量, 可理解为输入 可理解为作用在顶点 上的函数, 故 为长度为 的向量
其中 个特征向量组成的矩阵如下:
其中 为 特征值为 对应的特征向量, 类似
则 「在图上的傅里叶变换」的矩阵形式如下:
即:
同理可以推导 在图上的逆傅里叶变换:
GCN模型
上面已经得出: 类比得到图上卷积:
类比得到图上卷积:
其中 :
其中 为 的参数。
则可得:
=
由此可得:
其中 为激活函数, 就是「卷积核」,注意 为特征值组成的对角矩阵,所以 也是对角的,可以将卷积核记为如下形式
❝这里面的 就是我们要定义的卷积核具体形式
❞
这里面的参数 即为模型需要学习的卷积核参数。
论文中将 ,也即
❝为 个shape相同的矩阵相加,结果还是矩阵形式 注意上式中不同的特征值共享相同的参数 ,做到了参数共享
❞
继续推导可得:
❝注意得到的还是 个矩阵相加形式
❞
可得:
好了,直观上看这样做有以下几个优点:
卷积核只有 个参数,一般 远小于 ,参数的复杂度被大大降低了。 矩阵变换后,直接用拉普拉斯矩阵 替换,计算 时间复杂度还是
切比雪夫多项式及其捕捉局部特征
可以利用切比雪夫多项式来逼近卷积核函数:
其中 表示切比雪夫多项式, 表示模型需要学习的参数, 表示re-scaled的特征值对角矩阵,进行这个shift变换的原因是Chebyshev多项式的输入要在 之间,因此
由 可得:
其中
在实际运算过程中,可以利用Chebyshev多项式的性质,进行「递推」:
那么这种切比雪夫展开式如何体现其"localize" 呢?可以看看下面这个简单例子
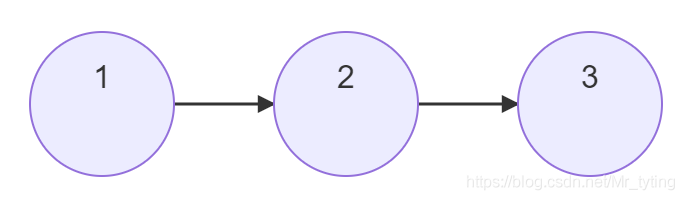
可以由上面这个简单的graph得到图的拉普拉斯矩阵
当 时,卷积核为 :
❝显然K=0时,卷积核只能关注到每个节点本身
❞
当 时,卷积核为 :
❝K=1时,卷积核能关注到每个节点本身与其一阶相邻的节点
❞
当 时,卷积核为 ,其中 :
❝K=2时,卷积核能关注到每个节点本身与其一阶相邻和二阶相邻的节点
❞
显然由上面推导可知:「切比雪夫多项式的项数,就是图卷积的感受野 」参数共享机制:「同阶共享相同参数,不同阶的参数不一样」。
Graph Coarsening(图粗化)
图的粗化可以理解为cnn中的pooling操作,这里面将相似的顶点合并成一个超级顶点。
论文中采用一种贪心(Graclus)算法来计算给定图的粗化结果,在每个coarsening level(可能存在多次粗化),使用一个unmarked的顶点 ,将这些顶点 与unmarked的邻居 相互匹配,找到
这两个匹配上的顶点然后mark一下,使用他们的权重的和 来作为粗化后的权重。一直重复这个过程,知道所有的点都被marked。
❝这里面相当于pool_size=2
❞
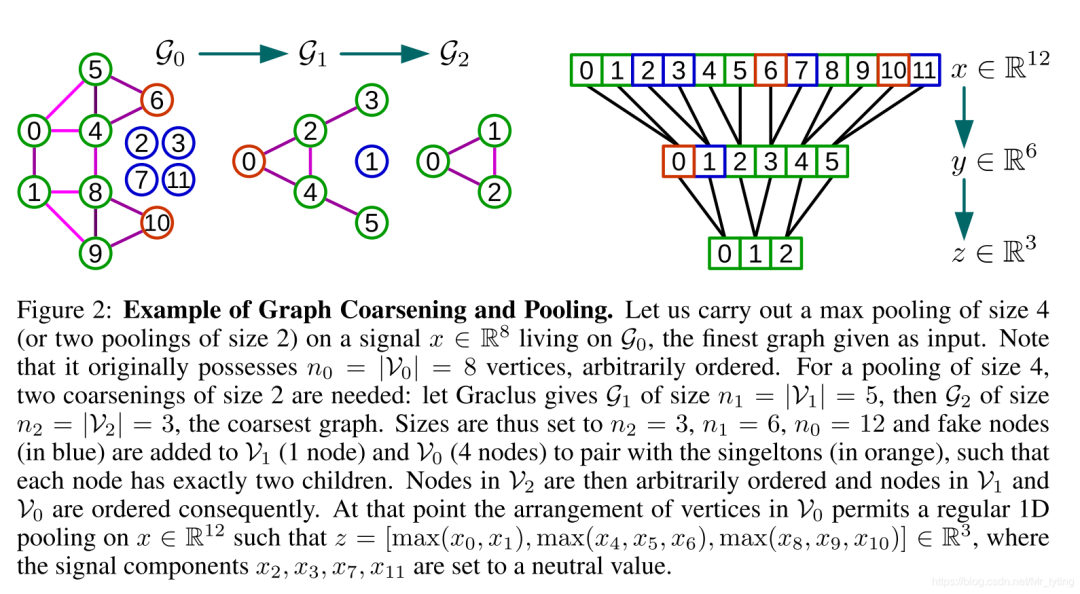
中两两类似的顶点合并,[0,1],[4,5], [8,9],6, 10合并重排成 中的0, 2, 4, 3, 5顶点 中的0, [2, 3], [4, 5] 顶点 合并重排成 中的 0, 1, 2顶点 为了能在1D数据上能方便的进行池化,需要给每个顶点配备两个子节点,如果该顶点有两个顶点则无需配备,否则需要配备一个或2个 。由 可知, 需要补充1 个 , 需要补充4 个 ,例如上图的右半部分图。 有12顶点后,可以在1D上很方便的pooling。 在 处,当使用 的时候, 初始化为0。这些 并不相连,故初值并不影响卷积操作结果,但是这些 确实增加了计算消耗,但是实践发现,Graclus算法里面的singletons很少。
❝图粗化的目的就是找到合适的填充fake node方式,方便后面在1D数据上pooling
❞
文本分类实验(Text Categorization on 20NEWS)
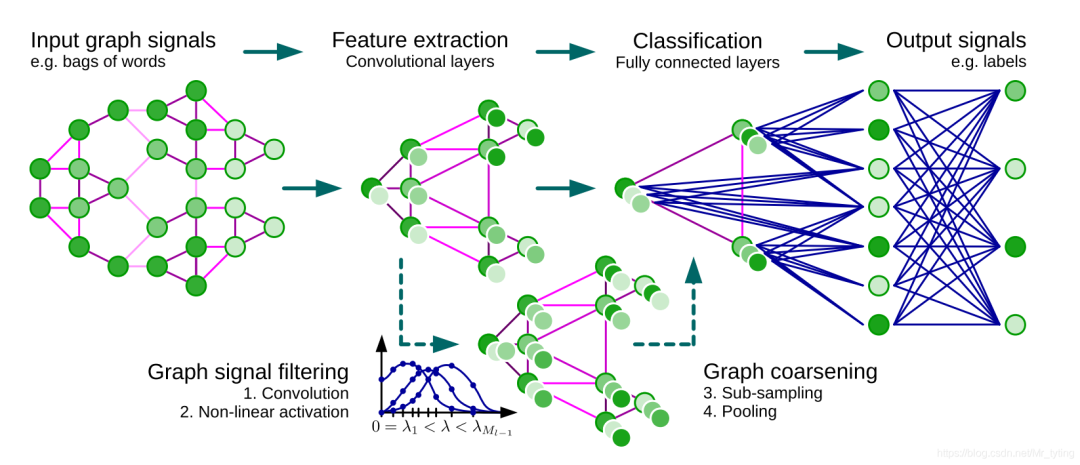
上面大概的把gcn的数学原理总结了一遍,来看看代码中 gcn是如何应用在文本分类这个task上的。
18846个text document【11314训练,7532测试】 20个类别 选取出现频次最高的1000个token作为词袋,每个document 用这个bag of words表示
数据预处理步骤
选取出现频次最高的1000个token作为词袋,每个文档用这个bag of words来表示 gensim.models.Word2Vec学习词的embeding矩阵,embed_size=100 计算词袋内两两词之间相似度,相似度矩阵shape=[1000, 1000] 相似度矩阵每行相当于一个顶点,将每行相似度最小的16个对应位置设置为0,剩余位置随机填1,由此构成邻接矩阵 对上面得到的邻接矩阵进行多层粗化,倒推每个coarsen_level应该填充多少个fake node 对train_data,test_data中每个样本填充相应数量的fake node,「其实就是对每个样本添加额外的零特征」
❝代码中顶点数量M_0 = |V| = 1000 nodes (0 fake node added),边数量|E| = 11390 edges 其实就是以词袋内每个token作为图上的顶点,以token之间相似度来随机构造边
❞
模型部分
表示一个batch的样本,论文代码中
这里以以下参数为例
name = 'cgconv_fc_softmax'
params = common.copy()
params['dir_name'] += name
params['regularization'] = 0
params['dropout'] = 1
params['learning_rate'] = 0.1
params['decay_rate'] = 0.999
params['momentum'] = 0
params['F'] = [5]
params['K'] = [15]
params['p'] = [1]
params['M'] = [100, C]
model_perf.test(models.cgcnn(L, **params), name, params,
train_data, train_labels, val_data, val_labels, test_data, test_labels)
params['F'] :表示卷积核的输出维度 params['K']:切比雪夫多项式数 params['p'] :每层池化的pool_size params['M'] = [100, C]: 表示先过100个神经元的fc,再在C=20个类别上做softmax
def _inference(self, x, dropout):
# Graph convolutional layers.
x = tf.expand_dims(x, 2) # N x M x F=1
for i in range(len(self.p)):
with tf.variable_scope('conv{}'.format(i+1)):
with tf.name_scope('filter'):
## filter表示切比雪夫的卷积过程
# self.L[i]表示当前level邻接矩阵的拉普拉斯矩阵
# self.F[i] 当前level卷积操作的输出维度
# self.K[i] 当前level卷积切比雪夫展开项数
x = self.filter(x, self.L[i], self.F[i], self.K[i])
with tf.name_scope('bias_relu'):
x = self.brelu(x)
with tf.name_scope('pooling'):
x = self.pool(x, self.p[i])
# Fully connected hidden layers.
N, M, F = x.get_shape()
x = tf.reshape(x, [int(N), int(M*F)]) # N x M
for i,M in enumerate(self.M[:-1]):
with tf.variable_scope('fc{}'.format(i+1)):
x = self.fc(x, M)
x = tf.nn.dropout(x, dropout)
# Logits linear layer, i.e. softmax without normalization.
with tf.variable_scope('logits'):
x = self.fc(x, self.M[-1], relu=False)
return x
切比雪夫过程
def chebyshev5(self, x, L, Fout, K):
N, M, Fin = x.get_shape()
N, M, Fin = int(N), int(M), int(Fin)
# Rescale Laplacian and store as a TF sparse tensor. Copy to not modify the shared L.
L = scipy.sparse.csr_matrix(L)
L = graph.rescale_L(L, lmax=2)
L = L.tocoo()
indices = np.column_stack((L.row, L.col))
L = tf.SparseTensor(indices, L.data, L.shape)
L = tf.sparse_reorder(L)
# Transform to Chebyshev basis
x0 = tf.transpose(x, perm=[1, 2, 0]) # M x Fin x N
x0 = tf.reshape(x0, [M, Fin*N]) # M x Fin*N
x = tf.expand_dims(x0, 0) # 1 x M x Fin*N
def concat(x, x_):
x_ = tf.expand_dims(x_, 0) # 1 x M x Fin*N
return tf.concat([x, x_], axis=0) # K x M x Fin*N
if K > 1:
x1 = tf.sparse_tensor_dense_matmul(L, x0)
x = concat(x, x1)
for k in range(2, K):
x2 = 2 * tf.sparse_tensor_dense_matmul(L, x1) - x0 # M x Fin*N
x = concat(x, x2)
x0, x1 = x1, x2
x = tf.reshape(x, [K, M, Fin, N]) # K x M x Fin x N
x = tf.transpose(x, perm=[3,1,2,0]) # N x M x Fin x K
x = tf.reshape(x, [N*M, Fin*K]) # N*M x Fin*K
# Filter: Fin*Fout filters of order K, i.e. one filterbank per feature pair.
W = self._weight_variable([Fin*K, Fout], regularization=False)
x = tf.matmul(x, W) # N*M x Fout
return tf.reshape(x, [N, M, Fout]) # N x M x Fout
pool过程:
def mpool1(self, x, p):
"""Max pooling of size p. Should be a power of 2."""
if p > 1:
x = tf.expand_dims(x, 3) # N x M x F x 1
x = tf.nn.max_pool(x, ksize=[1,p,1,1], strides=[1,p,1,1], padding='SAME')
#tf.maximum
return tf.squeeze(x, [3]) # N x M/p x F
else:
return x
可以看出加了fake node后,可以直接在输入矩阵上做pool
实验结果

个人总结
本论文旨在将图像上的卷积操作类比到graph上的卷积,做到了 「参数共享,局部特征」 cnn的两大核心特性,做法比较巧妙。
参考文献
http://papers.nips.cc/paper/6081-convolutional-neural-networks-on-graphs-with-fast-localized-spectral-filtering.pdf https://github.com/mdeff/cnn_graph http:/www.youtube.com/watch%3Fv%3Dc0MR-vWiUPU https://www.zhihu.com/question/54504471/answer/332657604 https://zhuanlan.zhihu.com/p/54505069 https://www.zhihu.com/column/c_1131513793020334080(强烈推荐)
Reference
GCN: http://papers.nips.cc/paper/6081-convolutional-neural-networks-on-graphs-with-fast-localized-spectral-filtering.pdf
[2]GCN-code: https://github.com/mdeff/cnn_graph
[3]如何通俗易懂地解释卷积?: https://www.zhihu.com/question/22298352
[4]拉普拉斯矩阵与拉普拉斯算子的关系: https://zhuanlan.zhihu.com/p/85287578
往期精彩回顾
