安全多方计算中常用的算法

“两个百万富翁都想比较到底谁更富有，但是又都不想让别人知道自己有多少钱。在没有可信的第三方的情况下如何进行？”这个问题就是著名的姚式百万富翁问题，此问题开创了安全多方计算领域。

1：安全多方计算

安全多方计算最初是针对一个两方安全计算问题，即所谓的“百万富翁问题”而被提出，并于1982年由姚期智提出和推广。安全多方计算的目的是协同的从每一方的隐私输入中计算函数的结果，而不用将输入展示给其他方。

安全多方计算具有以下特征：

• 隐私性(Privacy): 这是最重要的一点, 任何参与方不能获得任何所规定的输出之外的信息;

• 输入独立性(Input independence): 各个参与方必须独立选择自己的输入, 即不能根据其他参与方的输入来选择自身的输入;

• 输出一致性(Output consistency): 如果某个参与方获得了输出, 则所有参与方都将获得相同的输出.

通常安全多方计算能够通过三种框架来实现，不经意传输（Oblivious Transfer，OT）、秘密共享（Secret Sharing，SS）、阈值同态加密。其中不经意传输和阈值同态加密都使用了秘密共享的思想，所以秘密共享被广泛认为是安全多方计算的核心。

2：不经意传输（Oblivious Transfer，OT）

不经意传输是指数据发送方有n个数据，数据接收方接收其中的一个数据，且数据接收方不能获取其他的数据，数据发送方不知道接收方选择接收的数据具体是哪一个。一种比较实用的不经意传输方案，被称为1-2不经意传输。在1-2不经意传输中，发送方持有两个数据，接收方可以选择获取其中的一个，但是发送方并不知道接收方选择了哪一个数据。具体实现描述描述如下：

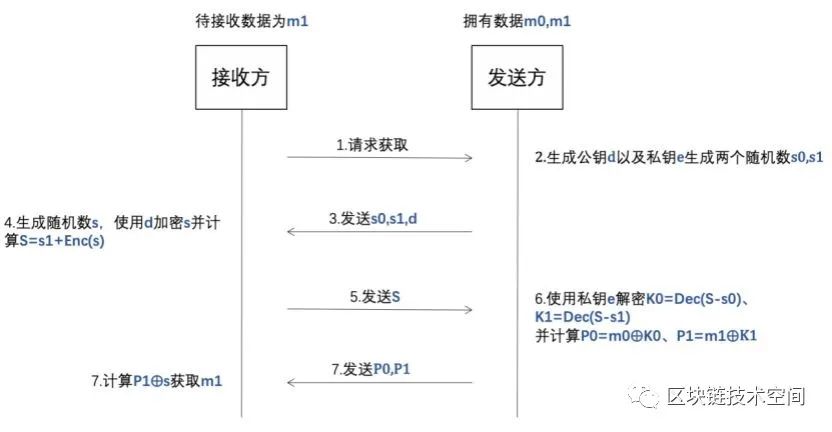
3：秘密分享

秘密分享（Secret Sharing，SS）是指通过将秘密值拆散成随机多份，并将这些数分发给不同方来隐藏秘密值得一种概念，每个参与方拿到的都是原始数据的一部分，一个或少数几个参与方无法还原出原始数据，只有把各自的数据凑在一起时才能还原出真实数据。

秘密共享主要包括算数秘密共享（Arithmetic Secret Sharing）、Shamir秘密共享、二进制秘密共享（Binary Secret Sharing）等方式。

• 假定A、B两方各有数x和y，其中将x和y进行分解，x = x1 + x2、y = y1 + y2

• 双方各自分享x2和y1，则A方计算z1 = x1+ y1，B方计算z2 = x2 + y2

• 将z1和z2共享，计算出z，显然有：z = x + y = z1 + z2 = x1 + x2 + y1 + y2

从而完成了加法运算。

3.1.2 乘法运算共享：

无条件的乘法运算分享被证明是不存在的，乘法运算的分享必须依赖于一个被分享的乘法三元组 <a, b, ab>，乘法三元组能够在离线阶段中产生，离线阶段可作为一个被信任的处理方。

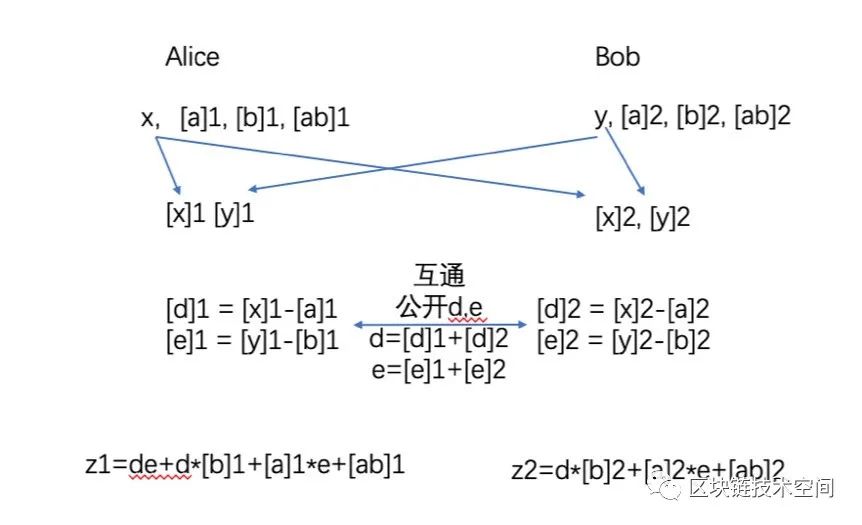
Alice和Bob分别持有x和y，他们得到了一对随机乘法三元组的分片。其中a = [a]1 + [a]2、b = [b]1 + [b]2、ab = a*b = [ab]1 + [ab]2。它们采用如下方法计算x、y的乘积。

• 各自将己方数据分享一个分片给对方，交换[x]2和[y]1。

• 各自通过加法分享并还原，分别得到x的盲化d = x - a ，y的盲化 e = y - b，并把d和e公开给对方。在此过程中, x, y, a, b均没有泄露。

• 此时x*y=(d+a)*(e+b)=de+[b]d+[a]e+[ab]，处于分享态的三元组放在了中括号内，可以看出问题已被转化为加法问题。

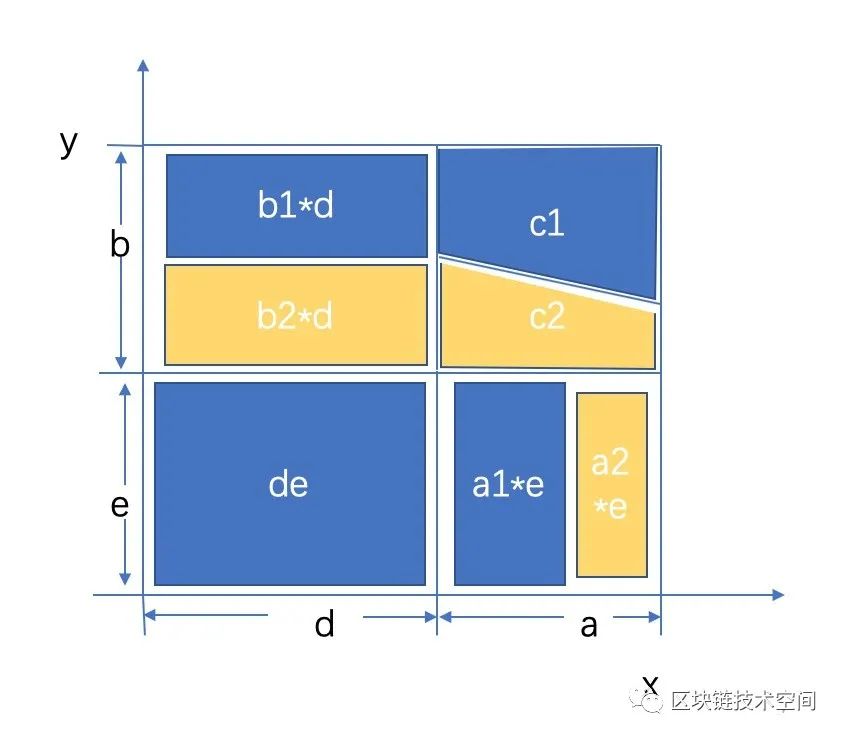
从下图看会更清楚，如同一块长方形的瓷砖被分成了7块，一方计算4块的面积，另一方计算3块的面积，如此就完成了乘法运算的加性分享。

3.2 Shamir秘密共享

下面介绍Shamir秘密分享，1979年Shamir提出了阈值秘密分享方案，该方案是基于拉格朗日插值法的一种支持n个参与方中的任意t个可以联合解开秘密数据的方案，具体方案如下：