【Go 刷 LeetCode】一棵树引发的算法题...
点击上方蓝字关注加小星星✨
涛哥给你我所有~
今天为大家讲解 LeetCode 第 108 题,是一道简单难度的题目。
题目描述
将一个按照升序排列的有序数组,转换为一棵高度平衡二叉搜索树。
本题中,一个高度平衡二叉树是指一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1。
示例:
给定有序数组: [-10,-3,0,5,9],
一个可能的答案是:[0,-3,9,-10,null,5],它可以表示下面这个高度平衡二叉搜索树:
0
/ \
-3 9
/ /
-10 5来源:力扣(LeetCode) 链接:https://leetcode-cn.com/problems/convert-sorted-array-to-binary-search-tree 著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
解题思路
这里,如果我们知道二叉树的中序遍历就是升序序列的话,那这道题就比较清晰了。(二叉树是一种很重要的数据结构,不了解的朋友自行去学习一下哦:)
选择中间位置左边的数字作为根节点,则根节点的下标 mid = (left + right) / 2。
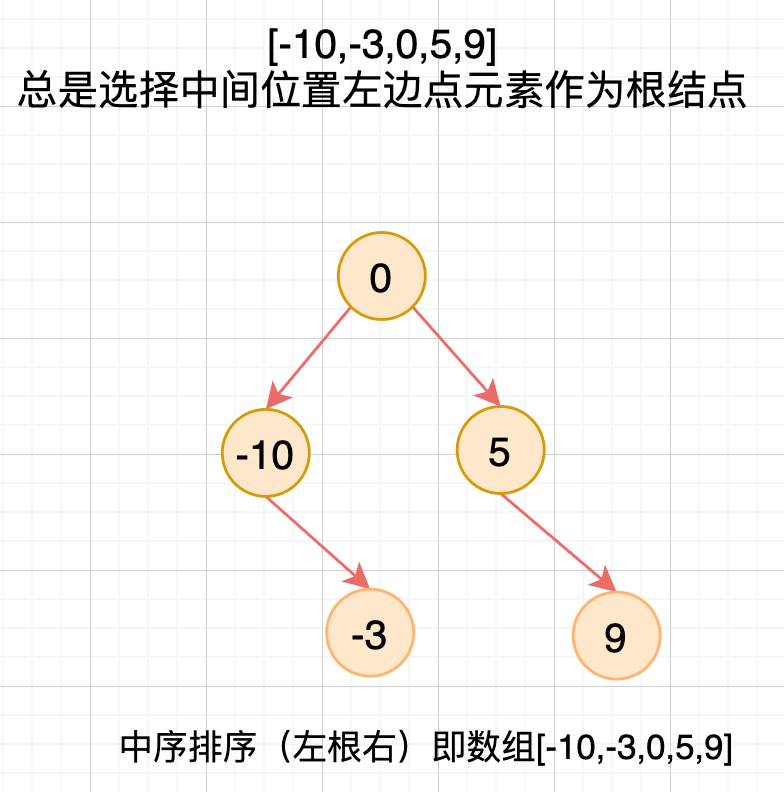
树结构多用递归实现。
代码实现
// go
//Definition for a binary tree node.
type TreeNode struct {
Val int
Left *TreeNode
Right *TreeNode
}
func sortedArrayToBST(nums []int) *TreeNode {
return helper(nums, 0, len(nums)-1)
}
func helper(nums []int, left int, right int) *TreeNode {
if left > right {
return nil
}
mid := (left + right) >> 1 // 等同于(left + right) / 2,位运算效率较高
// 注意:go 中的位运算符优先级高于加减,必须带括号!
root := &TreeNode{Val: nums[mid]}
root.Left = helper(nums, left, mid-1)
root.Right = helper(nums, mid+1, right)
return root
}
// java
class Solution {
public TreeNode sortedArrayToBST(int[] nums) {
return helper(nums, 0, nums.length - 1);
}
public TreeNode helper(int[] nums, int left, int right) {
if (left > right) {
return null;
}
// 总是选择中间位置左边的数字作为根节点
int mid = left + right >> 1; // Java 中的位运算符优先级低于加减,可以不带括号
TreeNode root = new TreeNode(nums[mid]);
root.left = helper(nums, left, mid - 1);
root.right = helper(nums, mid + 1, right);
return root;
}
}
这里另外多说一点,有个小坑。就是 Go 中的运算符优先级和其他语言(如我所知的Java,C)有不一样,搞不懂 Go 这里搞啥特殊,真是坑
这里顺便给出 Go 和 Java 的运算符优先级表
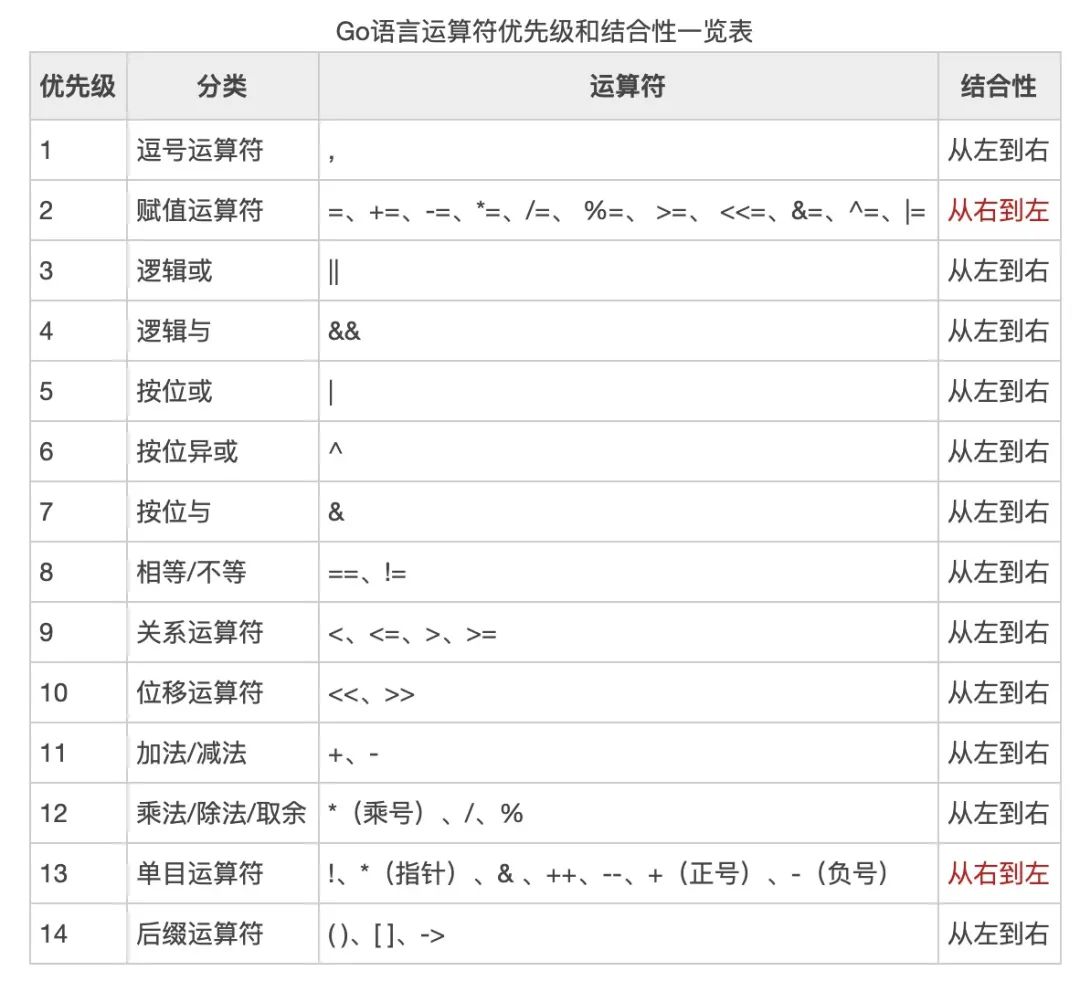

郑重声明:
所展示代码已通过 LeetCode 运行通过,请放心食用~
推荐阅读
喜欢本文的朋友,欢迎关注“Go语言中文网”:
Go语言中文网启用微信学习交流群,欢迎加微信:274768166,投稿亦欢迎
评论
