【图网络】如何用Python实现算法:规划图技术(GraphPlanner)
作者 | Debby Nirwan
作者 | Debby Nirwan
编译 | VK
来源 | Towards Data Science
介绍
规划图是为了解决经典人工智能规划方法(又称STRIPS规划器)的复杂性问题而发展起来的。我们需要实施两个主要部分:
规划图:数据结构
图规划:搜索算法,为我们找到解决方案
如果你不熟悉规划图,想了解更多,请查看我的以下帖子:
https://towardsdatascience.com/improving-classical-ai-planning-complexity-with-planning-graph-c63d47f87018
领域和问题表示
在我们开始实现之前,我们需要知道我们将如何表示规划域和规划问题。
规划图及其规划器与许多STRIPS规划器有相同的表示,因此我们将使用PDDL(规划域定义语言)来表示它们。下面是PDDL域文件的一个示例。
;; Specification in PDDL1 of the DWR domain
(define (domain dock-worker-robot-simple)
(:requirements :strips :typing )
(:types
location ; there are several connected locations in the harbor
robot ; holds at most 1 container, only 1 robot per location
container)
(:predicates
(adjacent ?l1 ?l2 - location) ; location ?l1 is adjacent ot ?l2
(atl ?r - robot ?l - location) ; robot ?r is at location ?l
(loaded ?r - robot ?c - container ) ; robot ?r is loaded with container ?c
(unloaded ?r - robot) ; robot ?r is empty
(in ?c - container ?l - location) ; container ?c is within location ?l
)
;; there are 3 operators in this domain:
;; moves a robot between two adjacent locations
(:action move
:parameters (?r - robot ?from ?to - location)
:precondition (and (adjacent ?from ?to) (atl ?r ?from) )
:effect (and (atl ?r ?to)
(not (atl ?r ?from)) ))
;; loads an empty robot with a container held by a nearby crane
(:action load
:parameters (?l - location ?c - container ?r - robot)
:precondition (and (atl ?r ?l) (in ?c ?l) (unloaded ?r))
:effect (and (loaded ?r ?c)
(not (in ?c ?l)) (not (unloaded ?r)) ))
;; unloads a robot holding a container with a nearby crane
(:action unload
:parameters (?l - location ?c - container ?r - robot)
:precondition (and (atl ?r ?l) (loaded ?r ?c) )
:effect (and (unloaded ?r) (in ?c ?l)
(not (loaded ?r ?c)) )) )
我们可以将PDDL看作JSON或XML之类的东西,这意味着我们需要一个解析器来反序列化用它编写的表示。当我在Github上搜索时,其中有几个出现了,但是有一个似乎很适合我们的项目pddlpy。
https://github.com/hfoffani/pddl-lib
但是,它在开发中不再活跃,我发现了一个bug和一些问题。因此,我决定使用它并编写一个适配器/包装器,这是一个薄层,我们添加它来修复错误并解决其他问题。
PDDL适配器
我们需要的代表如下:
世界的初始状态:数据类型为set
目标状态:数据类型为set
运算符(也称为操作)的列表,这些运算符已用实变量实例化:数据类型为List[Operator]
我们将只使用pddlpy库中的一个接口,DomainProblem()类构造函数。
我们需要提供上面列出的三个接口:初始状态、目标状态和运算符列表。
我们创建了一个名为PlanningProblem的类:
class PlanningProblem(object):
def __init__(self, dom_file: str, problem_file: str):
self._domain_file = dom_file
self._problem_file = problem_file
self._domain_problem = DomainProblem(self._domain_file,
self._problem_file)
self._initial_state = self._to_set_of_tuples(self._domain_problem.
initialstate())
self._goal_state = self._to_set_of_tuples(self._domain_problem.goals())
self._actions = self._get_ground_operators()
库提供的状态不是我们想要的正确数据类型,因此需要将它们转换为一组元组。
我们使用set()数据类型,以便以后实现数据结构和算法。因为在经典的人工智能规划中,我们大量使用集合论,我们应该使用set()数据类型来利用内置函数来加速我们的实现。我们将在下一节看到更多内容。
我们还必须创建一个运算符列表,我们称之为操作。下面是适配器的最终代码。
class PlanningProblem(object):
def __init__(self, dom_file: str, problem_file: str):
self._domain_file = dom_file
self._problem_file = problem_file
self._domain_problem = DomainProblem(self._domain_file,
self._problem_file)
self._initial_state = self._to_set_of_tuples(self._domain_problem.
initialstate())
self._goal_state = self._to_set_of_tuples(self._domain_problem.goals())
self._actions = self._get_ground_operators()
@staticmethod
def _type_symbols(variable_type, world_objects: dict):
# 如果变量类型是在world对象中找到的,
# 返回对象名称列表,如robr, robq
return (k for k, v in world_objects.items() if v == variable_type)
def _instantiate(self, variables, world_objects: dict):
variable_ground_space = []
for variable_name, variable_type in variables:
c = []
for symbol in self._type_symbols(variable_type, world_objects):
c.append((variable_name, symbol))
variable_ground_space.append(c)
return itertools.product(*variable_ground_space)
def _get_ground_operators(self) -> List[Operator]:
ground_operators = []
for operator in self._domain_problem.operators():
op = self._domain_problem.domain.operators[operator]
for ground in self._instantiate(op.variable_list.items(),
self._domain_problem.
worldobjects()):
st = dict(ground)
gop = Operator(operator)
gop.variable_list = st
gop.precondition_pos = set(
[a.ground(st) for a in op.precondition_pos])
gop.precondition_neg = set(
[a.ground(st) for a in op.precondition_neg])
gop.effect_pos = set([a.ground(st) for a in op.effect_pos])
gop.effect_neg = set([a.ground(st) for a in op.effect_neg])
ground_operators.append(gop)
return ground_operators
@staticmethod
def _to_set_of_tuples(state: Set[Atom]) -> Set[Tuple]:
set_of_tuples = set()
for atom in state:
tup = tuple(atom.predicate)
set_of_tuples.add(tup)
return set_of_tuples
@property
def initial_state(self):
return self._initial_state
@property
def goal_state(self):
return self._goal_state
@property
def actions(self):
return self._actions
我们现在可以使用这个类来解决规划领域和规划问题,并将重点放在数据结构和算法实现上。
规划图:数据结构
在这里我们将只看伪代码和方程,然后接下来的重点是将它们翻译成代码
以下是我们如何构建规划图的伪代码:
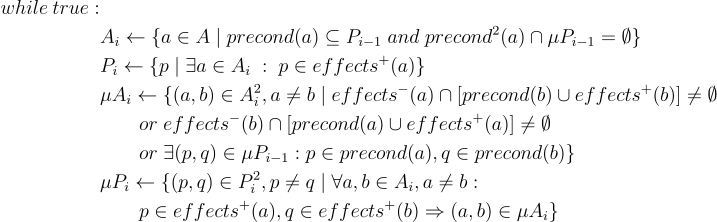
有四个步骤,我们一个接一个地讲。
计算动作
这是指以下步骤:
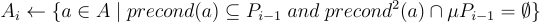
其中包括两部分:
对于PDDL适配器提供的所有操作,我们在当前状态下搜索可用的操作
我们确保那些可应用的操作的前提条件不在前提条件的互斥体中
class PlanningGraph(object):
def __init__(self, dom_file: str, problem_file: str):
self._planning_problem = PlanningProblem(dom_file, problem_file)
self._graph: Graph = Graph(visualize)
def compute_actions(self, gr: Graph):
graph_result = gr
level = gr.num_of_levels
# 计算 Ai
action_list = []
for action in self._planning_problem.actions:
if self._applicable(action, graph_result.prop[level - 1],
graph_result.prop_mutexes[level - 1]):
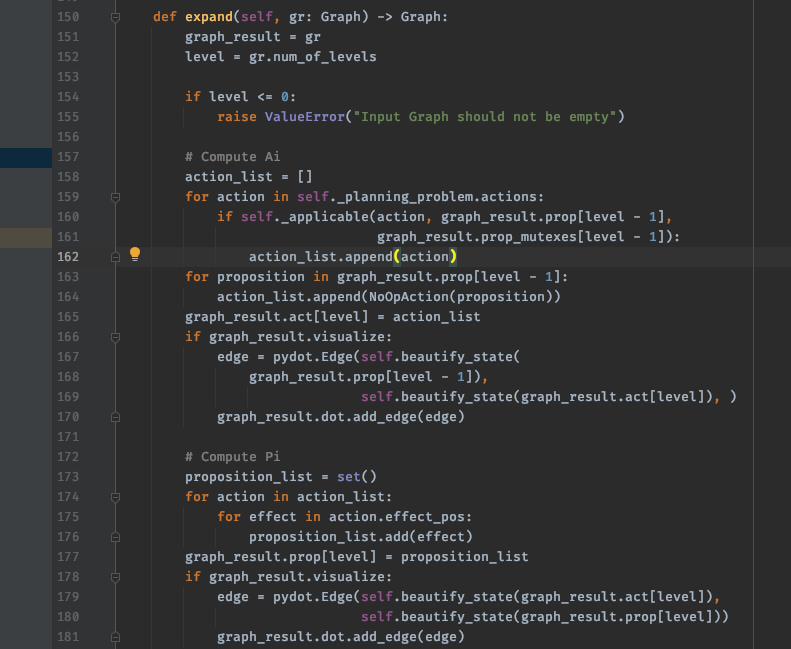
action_list.append(action)
graph_result.act[level] = action_list
@staticmethod
def _applicable(action, state, preconditions_mutex) -> bool:
if action.precondition_pos.issubset(state) and \
action.precondition_neg.isdisjoint(state):
applicable = True
if preconditions_mutex is not None:
for precondition in list(permutations(action.precondition_pos, 2)):
if precondition in preconditions_mutex:
applicable = False
break
else:
applicable = False
return applicable)
计算前提条件
下一步是计算前提条件,也就是这一步:
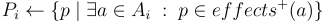
这一步非常简单:
class PlanningGraph(object):
def __init__(self, dom_file: str, problem_file: str):
self._planning_problem = PlanningProblem(dom_file, problem_file)
self._graph: Graph = Graph(visualize)
def compute_preconditions(self, gr: Graph):
graph_result = gr
level = gr.num_of_levels
proposition_list = set()
for action in action_list:
for effect in action.effect_pos:
proposition_list.add(effect)
graph_result.prop[level] = proposition_list
我们只存储计算出的动作效果。
计算操作互斥
该算法的下一步是计算Actions Mutex(操作互斥),这是一组相互抵消效果的操作。
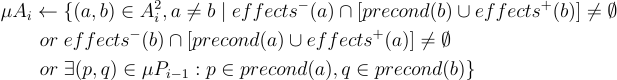
在这个等式中有三个部分,对于动作中所有可能的排列,我们希望在我们的列表中包括以下内容:
行动的消极影响会干扰另一方的积极影响或先决条件
第二部分是相同的,只是在另一个方向(b到a)
第三部分是它们的前提条件是互斥
class PlanningGraph(object):
def __init__(self, dom_file: str, problem_file: str):
self._planning_problem = PlanningProblem(dom_file, problem_file)
self._graph: Graph = Graph(visualize)
def compute_actions_mutex(self, gr: Graph):
graph_result = gr
level = gr.num_of_levels
action_mutex_list = []
for action_pair in list(permutations(action_list, 2)):
if self.compute_action_mutex(action_pair,
graph_result.prop_mutexes[level - 1]):
action_mutex_list.append(action_pair)
graph_result.act_mutexes[level] = action_mutex_list
@staticmethod
def compute_action_mutex(pair, preconds_mutex) -> bool:
a = pair[0]
b = pair[1]
# 两个动作是相互依存的
if a.effect_neg.intersection(b.precondition_pos.union(b.effect_pos)) \
!= set():
return True
if b.effect_neg.intersection(a.precondition_pos.union(a.effect_pos)) \
!= set():
return True
# 它们的先决条件互斥
if preconds_mutex is not None:
for mutex in preconds_mutex:
# (p, q)
p = mutex[0]
q = mutex[1]
if p in a.precondition_pos and q in b.precondition_pos:
return True
return False
计算互斥的前提条件
建立规划图的算法的最后一步是计算预条件互斥
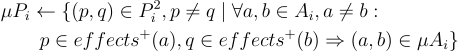
这意味着我们要寻找一对互斥的前提条件。它们是互斥的当且仅当:
对于同时产生p和q的所有操作对,它们都在actions Mutex列表中
没有同时产生p和q的单一操作
class PlanningGraph(object):
def __init__(self, dom_file: str, problem_file: str):
self._planning_problem = PlanningProblem(dom_file, problem_file)
self._graph: Graph = Graph()
def compute_preconditions_mutex(self, gr: Graph):
proposition_mutex_list = []
for proposition_pair in list(permutations(proposition_list, 2)):
if self.compute_precondition_mutex(proposition_pair, action_list, action_mutex_list):
if proposition_pair not in proposition_mutex_list:
swapped = (proposition_pair[1], proposition_pair[0])
if swapped not in proposition_mutex_list:
proposition_mutex_list.append(proposition_pair)
graph_result.prop_mutexes[level] = proposition_mutex_list
@staticmethod
def compute_precondition_mutex(proposition_pair, action_list, action_mutex):
p = proposition_pair[0]
q = proposition_pair[1]
for action in action_list:
if p in action.effect_pos and q in action.effect_pos:
# (p, q)不是互斥对象,如果它们都是由同一个动作产生的
return False
# 每一个产生p的动作
actions_with_p = set()
for action in action_list:
if p in action.effect_pos:
actions_with_p.add(action)
# 每一个产生q的动作
actions_with_q = set()
for action in action_list:
if q in action.effect_pos:
actions_with_q.add(action)
all_mutex = True
for p_action in actions_with_p:
for q_action in actions_with_q:
if p_action == q_action:
return False
if (p_action, q_action) not in action_mutex:
all_mutex = False
break
if not all_mutex:
break
return all_mutex
我们现在已经完成了构建数据结构的代码,规划图。为了帮助调试,可以使用pydot扩充代码以生成图形可视化。下面是一个例子。

搜索算法:GraphPlanner
我们现在已经准备好了数据结构,我们可以开始实现搜索算法,为我们的计划问题找到解决方案。
该算法是递归的,分为三个部分:
计划
提取
搜索
提取和搜索
这两个步骤是递归的,算法如下。第一部分是Extract:
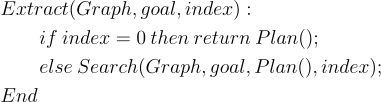
下一部分是Search:

这是这两个函数如何递归工作的示例:
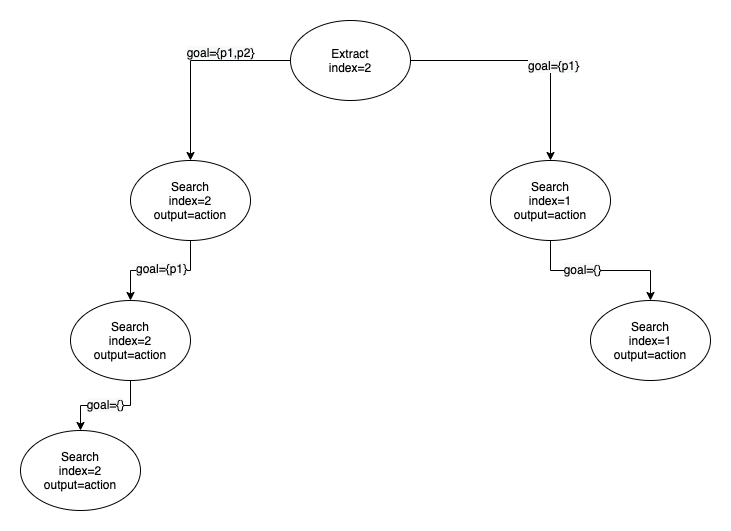
它递归地调用Search(),直到所有的命题都被解析,并调用Extract()进入规划图的下一级。
Python编写如下:
class GraphPlanner(object):
def __init__(self):
self._layered_plan: LayeredPlan = LayeredPlan()
self._mutex = {}
def _extract(self, gr: Graph, g: set, index: int):
if index == 0:
return Plan()
return self._search(gr, g, Plan(), index)
def _search(self, gr: Graph, g: set, plan: Plan, index: int):
if g == set():
new_goals = set()
for action in plan.plan:
for proposition in action.precondition_pos:
if 'adjacent' not in proposition:
new_goals.add(proposition)
extracted_plan = self._extract(gr, new_goals, index-1)
if extracted_plan is None:
return None
else:
self._layered_plan[index-1] = extracted_plan
self._layered_plan[index] = plan
return plan
else:
# 选择g中的任意p
proposition = g.pop()
# 计算解析器
resolvers = []
for action in gr.act[index]:
if proposition in action.effect_pos:
if plan.plan:
mutex = False
for action2 in plan.plan:
if (action, action2) in \
gr.act_mutexes[index]:
mutex = True
break
if not mutex:
resolvers.append(action)
else:
resolvers.append(action)
# 没有解析器
if not resolvers:
return None
# 选择非确定性,如果失败则回溯
while resolvers:
resolver = resolvers.pop()
plan.append(resolver)
plan_result = self._search(gr, g - resolver.effect_pos,
plan, index)
if plan_result is not None:
return plan_result
else:
plan.remove(resolver)
g.add(proposition)
return None
主程序
最后,我们到达了算法的最后一步、以下是主要步骤和入口点:

在某些情况下,我们需要计划更多的步骤来创建解决方案计划,我们需要展开规划图并重试搜索。
我们还需要添加一个额外的步骤,以确保算法在没有可能的解决方案时终止。下面是我们的最后一段代码:
class GraphPlanner(object):
def __init__(self):
self._layered_plan: LayeredPlan = LayeredPlan()
self._mutex = {}
def plan(self, gr: Graph, g: set):
index = gr.num_of_levels - 1
if not g.issubset(gr.prop[index]):
return None
plan = self._extract(gr, g, index)
if plan:
return self._layered_plan
if gr.fixed_point:
n = 0
try:
props_mutex = self._mutex[gr.num_of_levels - 1]
except KeyError:
props_mutex = None
if props_mutex:
n = len(props_mutex)
else:
n = 0
while True:
index += 1
gr = PlanningGraph.expand(gr)
plan = self._extract(gr, g, index)
if plan:
return self._layered_plan
elif gr.fixed_point:
try:
props_mutex = self._mutex[gr.num_of_levels-1]
except KeyError:
props_mutex = None
if props_mutex:
if n == len(props_mutex):
# 这意味着它已经稳定下来
return None
else:
n = len(props_mutex)
结尾
我意识到要描述实现这个算法的思想过程并不容易。但我希望至少你能对如何实现从等式、伪代码到Python代码的算法有一些基本的理解。
完整代码可在我的Github上获得,如下所示:
https://github.com/debbynirwan/planning_graph
往期精彩回顾
本站qq群851320808,加入微信群请扫码:
