【统计学习方法】第1章 统计学习方法概论(三)习题
点击上方“公众号”可订阅哦!
“这个公众号在我的新作品中帮助我毫不费力地使用了解决万有引力的问题。 我现在有更多时间站在树下,被苹果击中。”
Isaac Newton
本篇笔记是第1章的两道课后习题。
1
●
题目:
说明伯努利模型的极大似然估计以及贝叶斯估计中的统计学习方法三要素。伯努利模型是定义在取值为0与1的随机变量上的概率分布。假设观测到伯努利模型n次独立的数据生成结果,其中k次的结果为1,这时可以用极大似然估计或贝叶斯估计来估计结果为1的概率。
解答:
1 极大似然估计
模型:
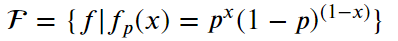
策略:最大似然估计
算法:
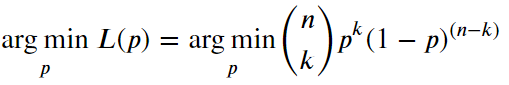
2 贝叶斯估计
模型:
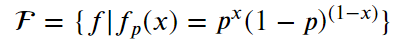
策略:求参数期望
算法:
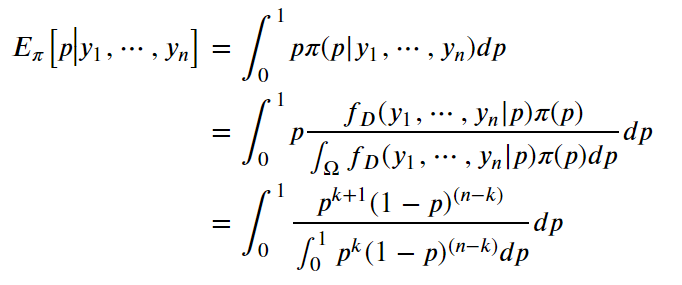
伯努利模型的极大似然估计:
定义P(Y=1)概率为p,可以得到似然函数:
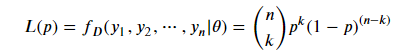
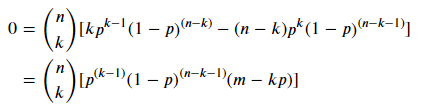
可以得到p的值为0,1,k/n
伯努利模型的贝叶斯估计
定义
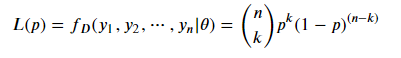
根据似然函数和先验概率密度函数,可以求解
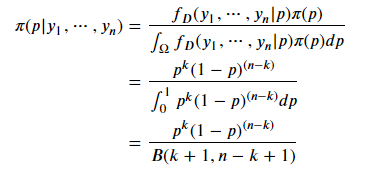
所以

所以,
2
●
题目:
通过经验风险模型最小化推导极大似然估计。证明模型是条件概率分布,当损失函数是对数损失函数时,经验风险最小化等价于极大似然估计。
解答:
假设模型的条件概率分布是
极大似然估计的似然函数为:
两边取对数,
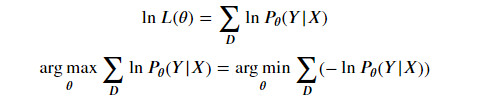
反之,经验风险最小化等价于极大似然估计,可通过经验风险最小化推导极大似然估计。
END
扫码关注
微信号|sdxx_rmbj
评论

