你想知道的A/B实验知识全在这里了
作者介绍
A/B实验中的基础知识
01
正交试验与互斥实验
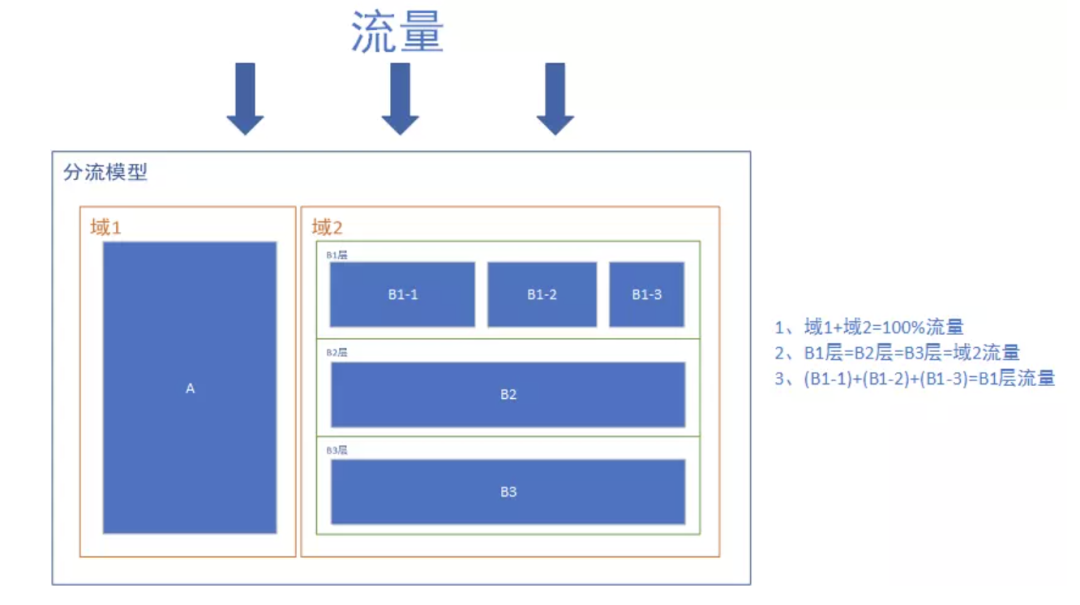
域1和域2流量进行了拆分,此时域1和域2是互斥的。一般是有相互干扰的实验需要进行流量互斥,比如同样是发促销券类活动,只是不同的业务团队发放的,那么域1和域2的流量就要拆分开,避免互相进行干扰,影响实验最终结果。
流量流过域2中的B1层、B2层、B3层时,流量都是与域2的流量相等,此时B1层、B2层、B3层的流量是正交的,比较典型的B1层、B2层、B3层是UI层、搜索结果层、广告结果层,这几层基本上是没有任何的业务关联度的,即使共用相同的流量(流量正交)也不会对实际的业务造成结果。
值得注意的是,流量流过域2中的B1层时,又把B1层分为了B1-1,B1-2,B1-3,此时B1-1,B1-2,B1-3之间又是互斥的。
02
实验分组
一般来说,至少有1个实验组A和1个对照组B,但是随着A/B测试的应用越来越广泛,并不局限于只有1个实验组A和1个对照组B,可能会有实验组A1、实验组A2和对照组B,甚至更多的实验组同时验证不同策略的效果。比如在实际的运营工作中,需要评估某个券的效果,这时候设置了3个组:
实验组1:用规则发券,所有目标用户群发放满200-20的品类券
实验组2:走模型策略,基于用户的标签属性发放不同门槛-面额的券,比如有人发放满150-10,有人发放满300-30
对照组:不进行任何发券动作
这样,根据实验组1和对照组进行比较能得出规则发券的效果,实验组2和对照组进行比较能得出模型策略发券效果,从而得出走模型策略相较于规则发券效果提升了多少。
03
假设检验
假设检验是先对总体参数提出一个假设值,然后利用样本信息判断这一假设是否成立。需要了解假设检验中的两个假设、两类错误。
两个假设
原假设H0:实验中想反对的假设
备择假设H1:实验中想予以支持的假设
两类错误
第一类错误:弃真错误,当原假设为真时拒绝原假设
第二类错误:取伪错误,当原假设为假时未拒绝原假设
04
A/B测试统计量
2.4.1 假设检验中的P值
P值即概率,反映某一事件发生的可能性大小。统计学根据显著性检验方法所得到的P值,一般以P<0.05 为有统计学差异。
2.4.2 假设检验中的显著性水平α
显著性水平是估计总体参数落在某一区间内,可能犯错误的概率,用α表示。小概率标准α和P值的关系如下:
如果P≤α,那么拒绝原假设
如果P>α,那么不能拒绝原假设
2.4.3 Z检验
检验方法有t检验、Z检验、χ2检验和F检验。在A/B实验中,主要是对样本均值进行检验,所以用t检验和Z检验。在样本数量比较大情况下,采用Z检验,A/B实验中双样本Z检验公式如下:

t检验:t检验常用于总体正态分布、总体方差未知或独立小样本平均数的显著性检验、平均数差异显著性检验。
Z检验:Z检验常用于总体正态分布、方差已知或独立大样本的平均数的显著性和差异的显著性检验。
2.4.4 置信区间
置信区间是用来对一个概率样本的总体参数进行区间估计的样本均值范围,它展现了这个均值范围包含总体参数的概率,这个概率称为置信水平。置信水平代表了估计的可靠度,一般来说使用95%的置信水平进行区间估计。置信区间可以辅助确定版本间是否有存在显著差异的可能性:如果置信区间上下限的值同为正或负,认为存在有显著差异的可能性;如果同时有负值和正值,那么则认为不存在有显著差异的可能性。
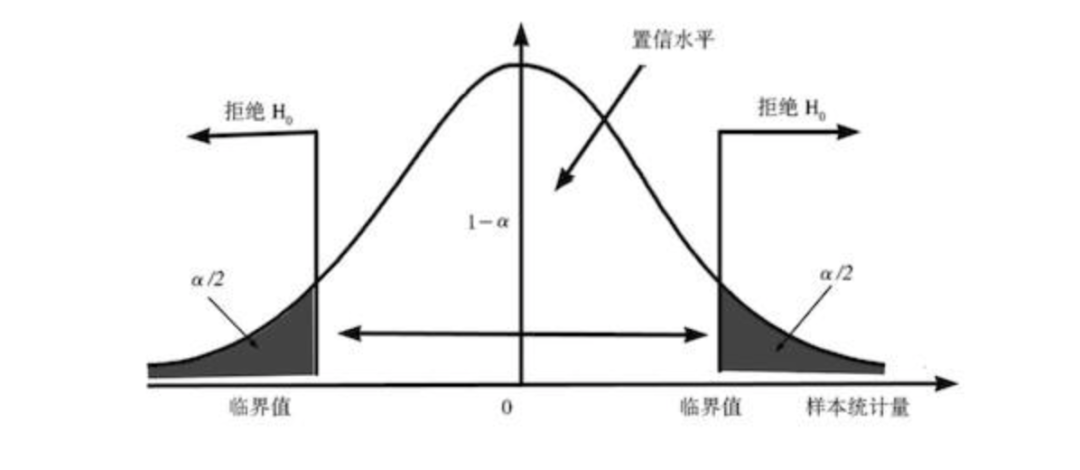
根据统计学的中心极限定理,样本均值的抽样分布呈整体分布,因此通过下面的公式可以计算出两个总体均值差的95%置信区间:
2.4.5 统计功效
当两个不同版本之间存在显著差异时,实验能正确做出存在差异判断的概率。可以理解为有多少的把握认为版本之间有差别。该值越大则表示概率越大、功效越充分。一般来说,设定最低的统计功效值为80%,统计功效的计算如下:
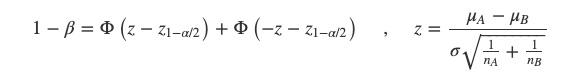
σ 是标准差
Φ是标准正态分布下某个X值对应的概率面积
α是一类错误概率
A/B实验步骤及案例分享
01
确认实验目标
业务团队目前正在做沉默用户召回,想验证不同的召回发券策略的效率,并在接下来的召回运营中推广使用效率最高的策略。此时的实验目标:找到召回沉默用户效率最高的策略。
02
设计实验
设计实验时需要明确目标用户、实验周期、最小样本量、用户分组、分流比例、分组策略等信息。
目标用户:过去30天-180天未下单老客
实验周期:测试1周,周期内不进行打散
最小样本量确定:输入原始的召回率、策略优化后的召回率以及显著性水平,网上有很多类似的工具,下面是来自https://www.eyeofcloud.com/124.html计算的结果,最少需要5300的样本量
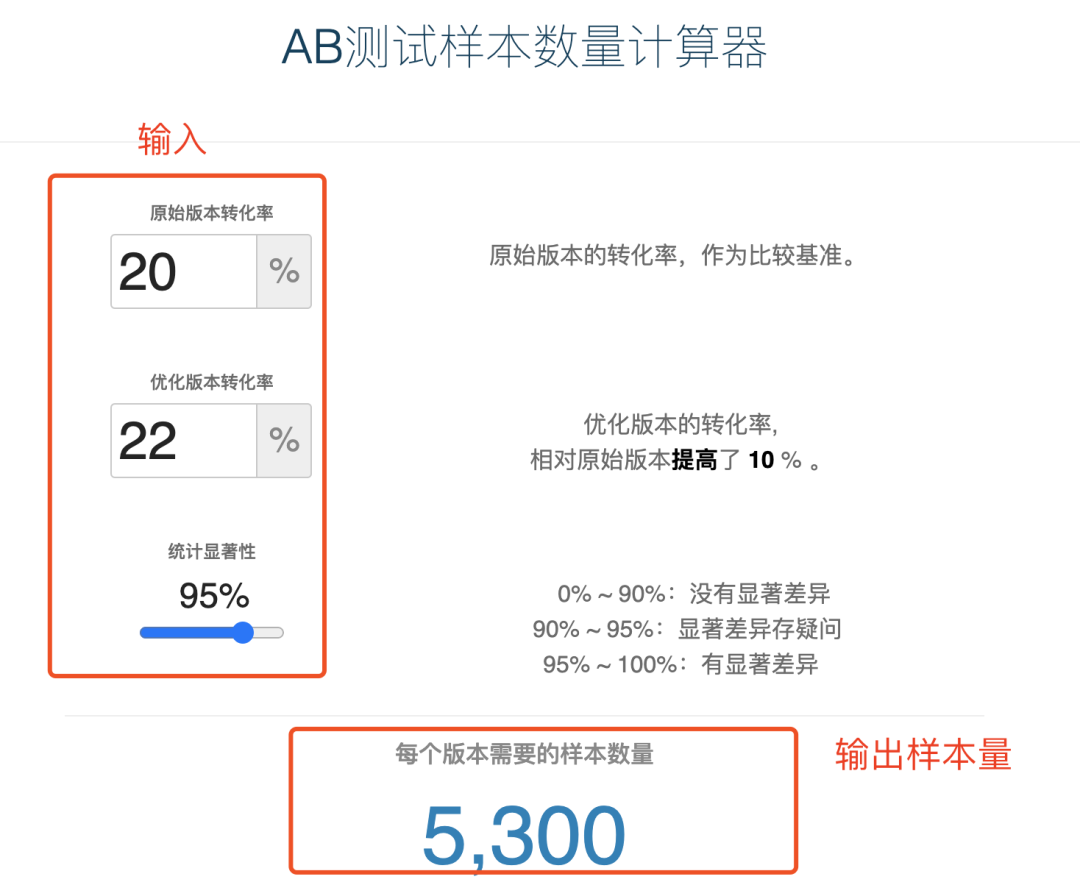
实验分组及策略:
分组 | 分流比例 | 沉默召回策略 |
实验组1 | 30% | 发放满20-5的优惠券,并通过精准营销短信触达 |
实验组2 | 30% | 发放满30-6的优惠券,并通过精准营销短信触达 |
实验组3 | 30% | 发放满40-10的优惠券,并通过精准营销短信触达 |
对照组 | 10% | 不进行任何策略 |
03
上线实验与过程监控
实验上线后,需要检测实验是否按照预期设定正常运行,在A/B实验中常出现的需要检查的问题有如下:
空白组是否真的空白的,有无空白组用户领取到实验组1、实验组2、实验组3发的券,如果发现有领券的,那需要排查分流系统问题(一般需要产研根据log信息找到当时为什么判定给该用户发券)
1个用户是否仅属于某一个组,有无存在多个组的情况
分流是否和预先设定的分流比例一致,误差1%也要寻找原因
实验样本是否是预先设定的目标实验样本,判断实验是否进行了用户筛选过滤,比如本实验是对沉默用户进行召回,有无近30天有交易的活跃用户也被发券,如果有那说明目标用户的圈选出问题,需要排查上下游看看是哪个环节出现问题
04
结果复盘之ROI评估
通过试验组1、实验组2、实验组3分别和对照进行对比,能得出3组策略的效率。ROI的分子是投入的总资源成本,产出可以是用户的原价交易额、单量、利润等信息,此处用原价交易额作为产出,来评估不同策略的召回效率,最终结果如下所示。可以看到:
3种召回策略ROI均置信,且ROI由高到底是实验组2(满30-6)>实验组3(满40-10)>实验组1(满20-5)
虽然单量最高的实验组1,但是由于实验组1发券的门槛低只有20元,导致最后的交易额增量不如实验组2和实验组3
虽然实验组2的交易额增量不如实验组3,但是实验组的2的成本低于实验组3,因此最后ROI比实验组3高

所以,通过该实验可以看出,在发放针对沉默用户发券的时候,需要同时考虑到门槛和面额,一方面低门槛会让用券的用户增加,但低门槛下客单较低,总原价交易额也就越低;另一方面面额影响用户转化的同时也影响投入成本。具体设置多少的门槛和面额最佳,还需要通过更多的A/B实验来判定。
后记
在A/B实验中,有以下3点需要注意的。
注意保证单一变量
A/B实验需要保证实验组样本和对照组样本是同样属性的,通过控制单一变量判断最终效果。但是在实际的过程中,有团队会在不同应用市场、不同渠道进行测试,比如测试2个投放策略,一个在快手测试,一个在抖音策略,这两个渠道的用户群里天然的就有差异,得出的数据是不可信的。正确的做法是在快手和抖音都用同一个策略,验证统一策略在不同渠道的效果,或者只在快手渠道进行不同策略的测试。
注意效率和规模
很多时候做A/B实验是对用户进行了筛选的,这个时候得出的ROI较高。但是这个策略一旦扩量到全部用户,ROI有可能就会降低。因此在说某个策略的ROI时,需要注意是否是小规模用户的效率,而不是整体用户的ROI。
注意新奇效应
在出某个新功能、新策略的时候,用户可能会比较感兴趣,这个时候效果较好,但是过一段时间用户新奇感觉消失。为了避免这种情况,需要在单一变量下,重复、长时地进行实验,得到长期稳定的结果。