【07】无人驾驶的规划
1.规划简介
在规划中,我们通过结合高精度地图、定位和预测来构建车辆轨迹。规划分为两部分,一部分为宏观规划,我们称为路线规划,另一部分是微观规划,我们称为轨迹规划。
1.1 路线规划
规划的第一步是路线规划,侧重于表达如何从地图上的一点前往另一点,在进行路径规划时,将地图数据作为输入,并输出可行驶的路径,手机导航的路径规划就是一个常见的例子,更具体的,我们从上海到杭州的自驾游中,我们选择怎么样的路线,这就是路线导航。 在自动驾驶中,通过路线规划模块处理该任务。
1.2 轨迹规划
我们通过路线导航,一旦构建出了高水平的路线,就可以放大至轨迹规划,而通过轨迹规划,就可以做出微妙的决策,以避开障碍物,并为乘客创造平稳的乘车体验。通俗来讲,我们从上海到杭州的自驾游中,我们虽然定了宏观的路线,但是在行驶中我们在什么地方变道、如何避让来往车辆,这就是轨迹规划需要处理的问题。 在自动驾驶中,我们通过规划模块处理该任务。
轨迹规划的目标是生成免碰撞和舒适的可执行轨迹,该轨迹由一系列点定义,每个点都定义了三个内容:
坐标
速度
到达时间
2.路线规划
当人们试图在地图上找到从A到B的路线时,通常会沿着道路追踪路径,以查看是否存在通往目的地的任何路径,这个过程称为搜索,可以想象一下玩走迷宫的游戏,通常是沿着道路走每一种可能性,最终得到想要的路径。
路径规划也通过搜索来查找路线,但是不同的是它使用了更加智能的搜索算法,在开始搜索之前,路径规划将地图数据格式化为“图形”的数据结构,该图形由节点和边缘组成,节点代表路段,边缘代表这些路段之间的连接,通常也会将节点称为Section,将边缘称为Connection。
看下边这张图,在交叉路口,汽车可以从node1移动到node2、node3或node4,反之亦然,我们可以对从一个节点到另一个节点所需的成本进行建模,例如,在现实中,拐过一个交叉路口比执行更费劲儿,所以从node1到node4的成本高于从node1到node3的成本。
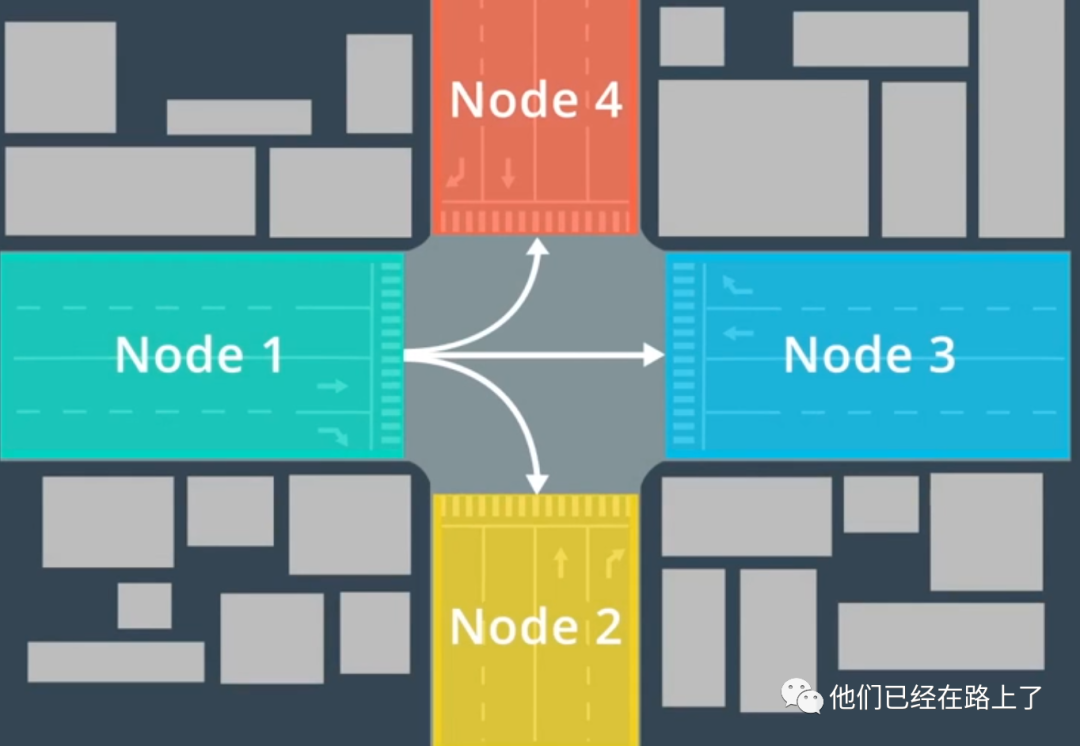
将地图转化成图形的好处在于在计算机科学领域中,人们已发现了许多用于在图形中查找路径的快速算法,一旦我们在图形中找到了一条最优路径,就可以轻松地将图形中的路径重新转换为地图上的路径。
那么接下来我们就了解一下路径处理的算法。
2.1 A*算法搜索最优路径
A* 是经典的路径查处理算法,我们来一起看看A*算法。
看下图,我们把每一个小方格都定义为一个节点,我们如何找到从红色点到绿色点的最佳距离,面对这个网格,我们可以很容易的找到网格中两个点之间的最短路径,但这对于计算机而言并不容易,计算机必须检查通往目的地的任何路径。
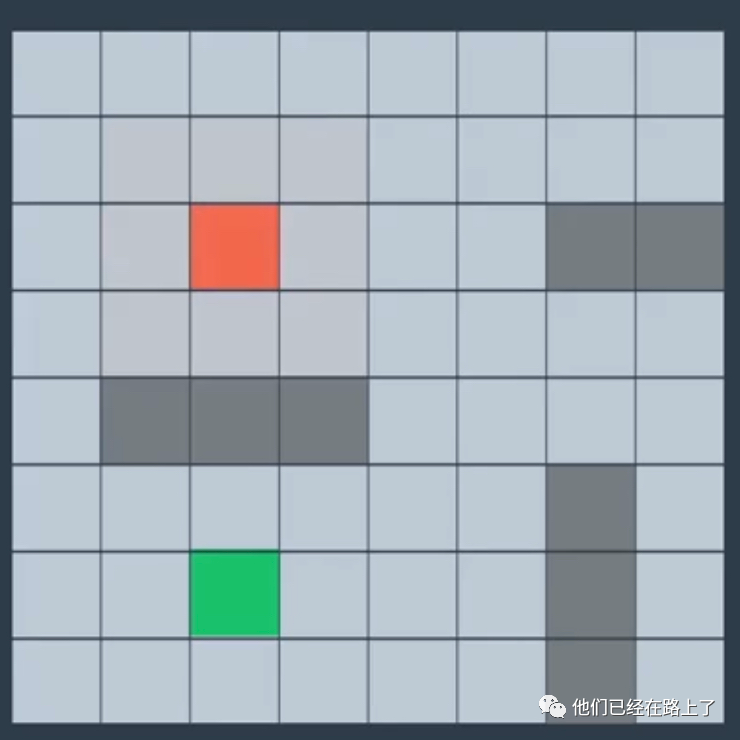
计算机会从起点开始,竭尽所能的尝试所有可能的路径,以找到最短的路径,但是这个过程会消耗大量的时间,尤其是在地图非常大的时间。
我们以红色的节点为例,我们有8个用于下一步的选项:
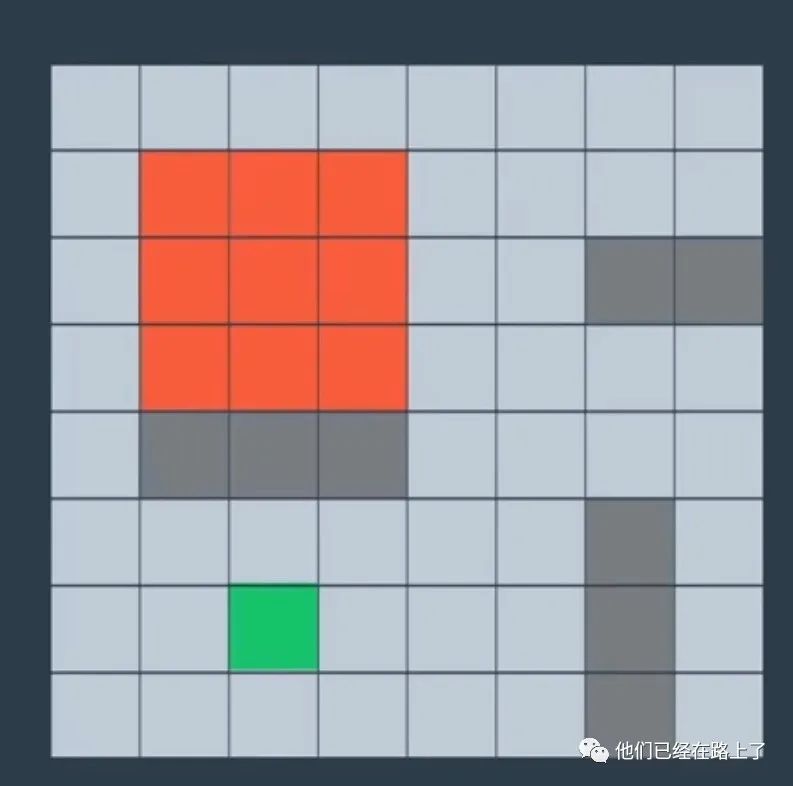
对于这8个选项而言,他的下一步依然有另外8个选项,抛开已经经过的节点,还有13个选项:

如果我们展开所有的节点,搜索量将指数型的增长,即使是最快的计算机,可能也无法处理。这时候我们需要采用更好的策略来寻找最佳路线。
从初始节点开始,我们需要确定8个相邻的节点中哪个是最有希望的候选节点,对于每个候选节点,我们考虑两件事情:
首先,我们计算从开始节点(起点)到候选节点(下一个点)的成本。
其次,我们估计从候选节点前往目的地的成本。
这个过程中,计算前往候选节点的成本很容易,因为他已经与我们相临了,比如我们走到一个路口,直行、左转、右转三个对我们而言最简便的是哪个,这就很清晰。难点在于计算从候选节点到目的地的成本。针对这个问题,我们可以通过一些简单的计算,估计出从候选节点到目的地的距离。
我们使用变量g和h来表示每个成本:
g表示从开始节点前往候选节点的成本;
h表示从候选节点到前往目的地的估计成本。
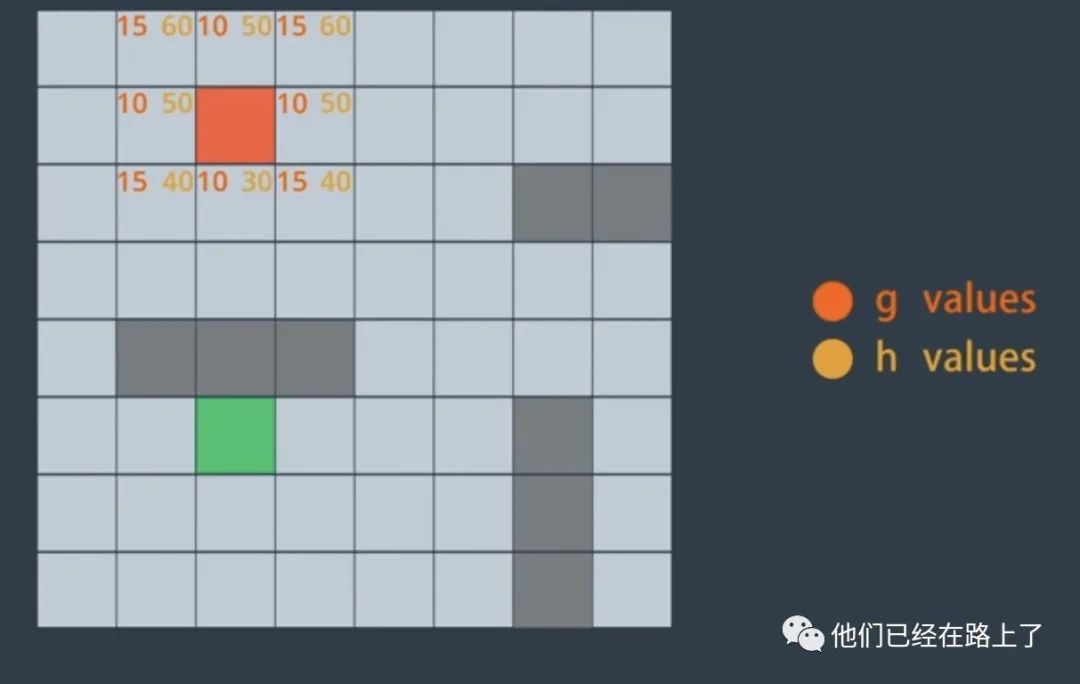
根据我们的情况,我们可以自定义成本估算的方式,例如,交通堵塞会增加前往目的地的成本,所以交通拥堵的路径具有更高的成本,映射到网格图里那就是候选节点的h值更高。
我们通过添加g和h来计算总和,来得到f值。
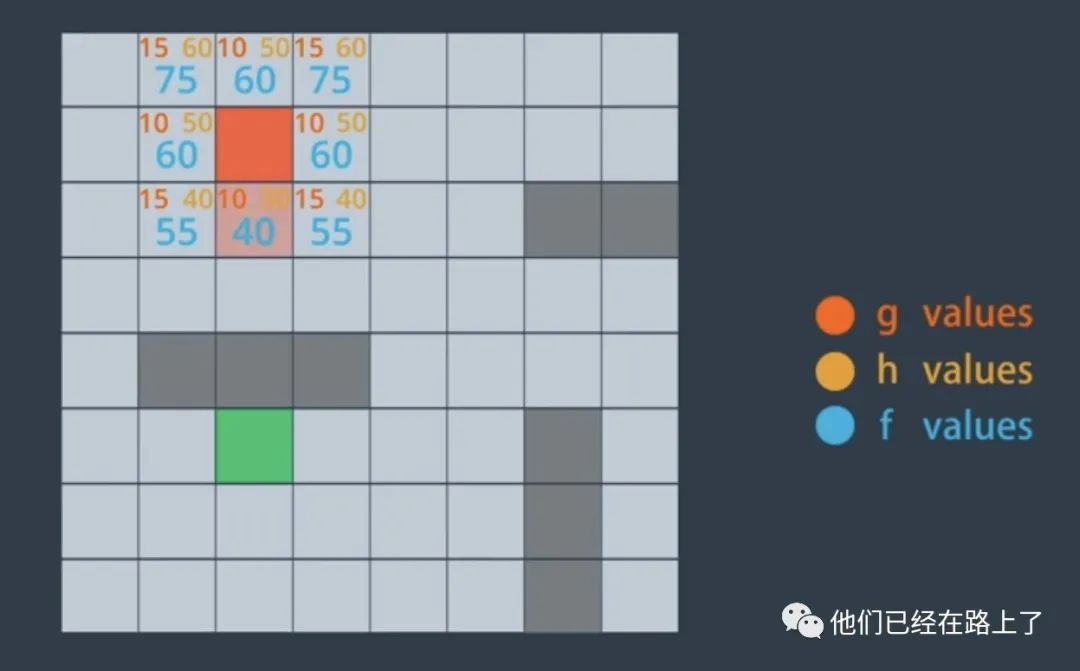
而所谓最佳候选点,就是f值最小的节点,每当我们抵达新的节点的时候,我们就通过重复此过程来选择下一个节点,而且总是选择我们尚未访问过的节点,最终我们得到了一条f值最小的路径,这就是A*算法。
2.2 从网格到真实地图
现在我们来考虑一下真实世界中的地图,假设我们到达了一个交叉路口,我们可以沿着公路直走、右转或左转,我们看下边这张图,我们把这张地图转换成具有三个候选节点的图形:
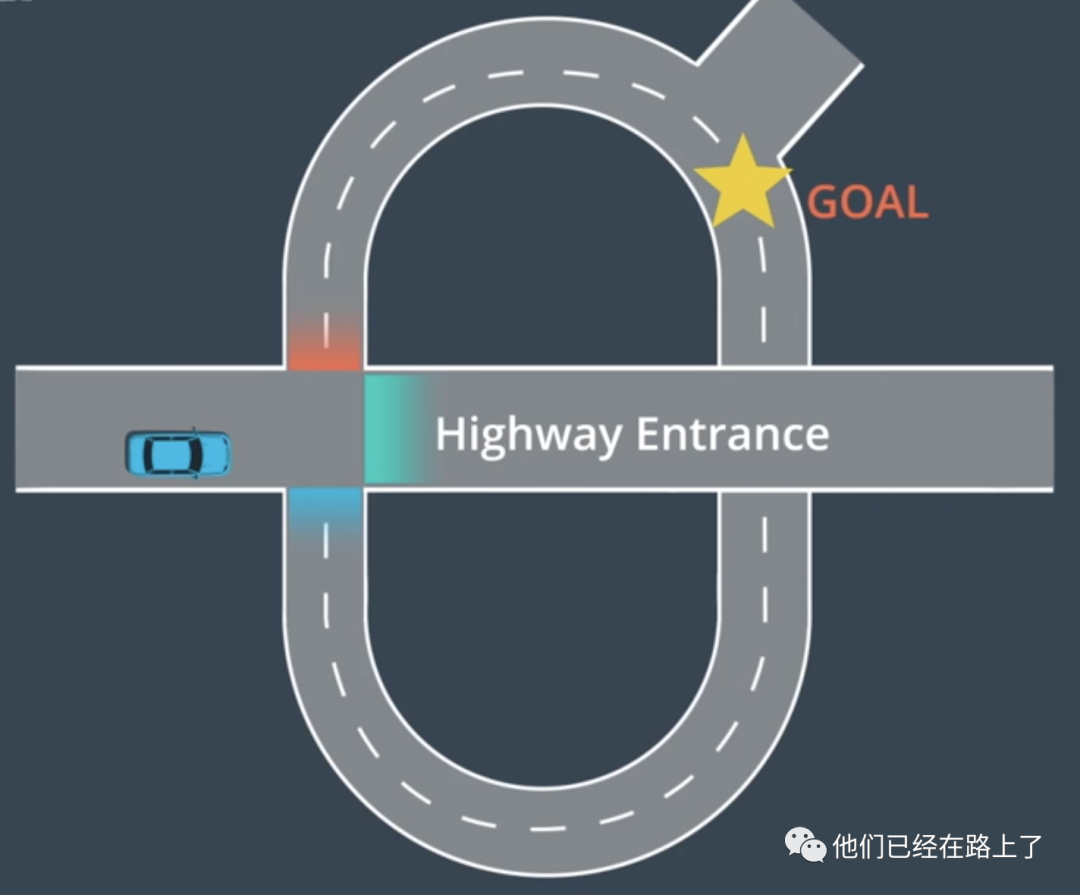
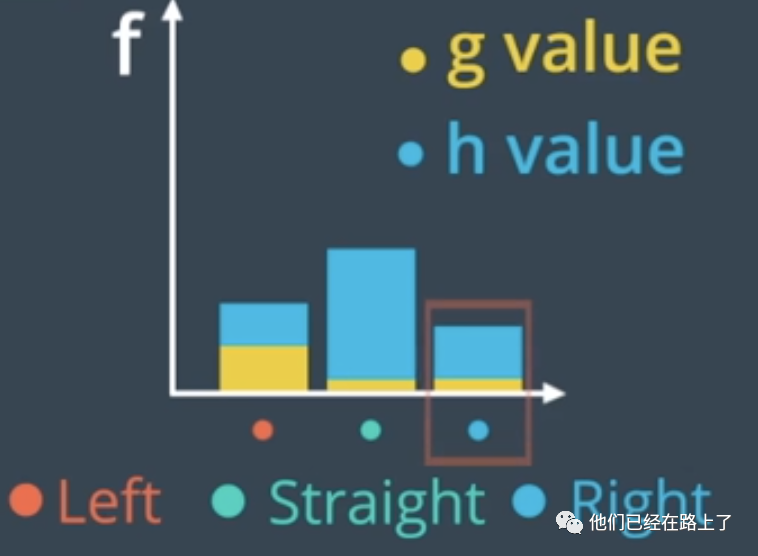
然后我们对每个选项进行评估,在实践中,我们拐过交叉路口比较费劲儿,所以我们给转弯分配更高的g值,接下来,我们根据道路的长度,给每一种路线分配一个h值,我们将g和h相加,最终得到了一个最低的f值,这就是对应的最短路径。
3.从路线到轨迹
接下来我们看从路线到轨迹的规划,宏观的地图路线只是规划过程的一部分,好比我们从上海到杭州走哪条高速这只是路线级别的规划,我们仍然需要构建沿着这条路线前进的低等级轨迹,也就是说微观的轨迹,宏观的规划是基于地图的属性进行判断的,就像上边讲的,根据道路长度、拥堵、路口等,微观的规划就需要处理很多不属于地图的物体,例如其他车辆、行人、障碍物等,当我们在道路上与一辆正在掉头的汽车相遇,我们就需要与这辆汽车互动,这种场景需要更低级别、更高精度的规划,而这个级别的规划就称之为轨迹生成。
3.1 轨迹概述
轨迹生成的目标是生成一系列路径点所定义的轨迹,我们为每一个路径点分配一个时间戳和速度:
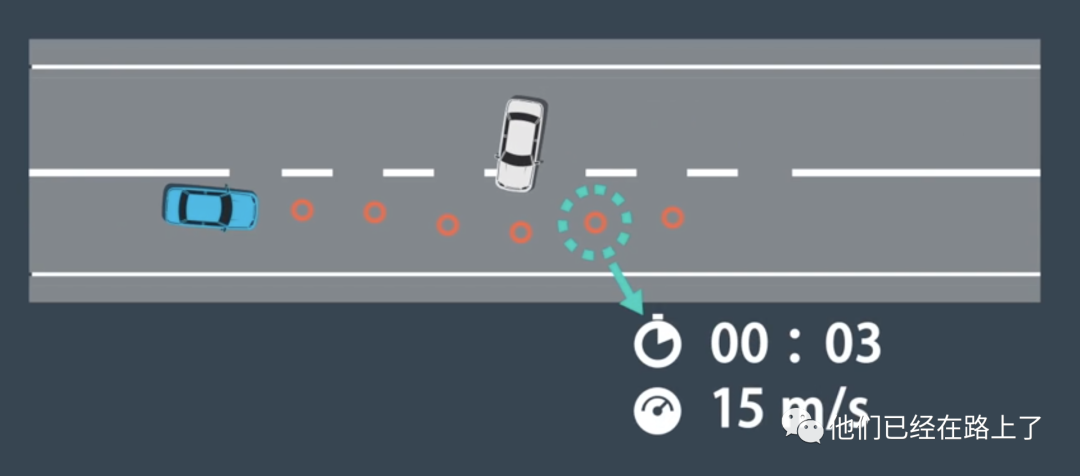
然后将这些点用一条曲线拟合起来,生成轨迹的几何表征。由于移动的障碍物可能会暂时阻挡部分的路段,轨迹中的每个路点都有时间戳,我们可以将时间戳与预测模块的输出相结合,以确保在我们计划通过时,轨迹上的每一个点都未被占用。这些时间戳创建了一个三维的轨迹,也就是每个路径点的横纵坐标和时间,我们还为每个路径点指定了一个速度,速度用于确保车辆按时到达每个路径点。
3.2 轨迹的评估
在现实中,规划面临多种约束,大体上我们可以分为四个要求:
轨迹应能免于碰撞,这意味着必须无障碍物;
轨迹让乘客感觉到舒适,因此路径点之间的过渡以及速度的任何变化都必须要平滑;
路径点对于车辆而言应该切实可行才行,例如高速移动的车辆如果猛打方向会造成侧翻,相信会开车的同学都知道,驾校教练会告诉你不要猛打方向,对于轨迹生成同样,我们不能构建这种不可行的轨迹;
轨迹应该合法,我们需要遵守不同地区的交通法规,确保轨迹的合法性。
我们再思考一个问题,在道路上任何两点之间,其实是有多个满足上述要求的轨迹的,如下图:
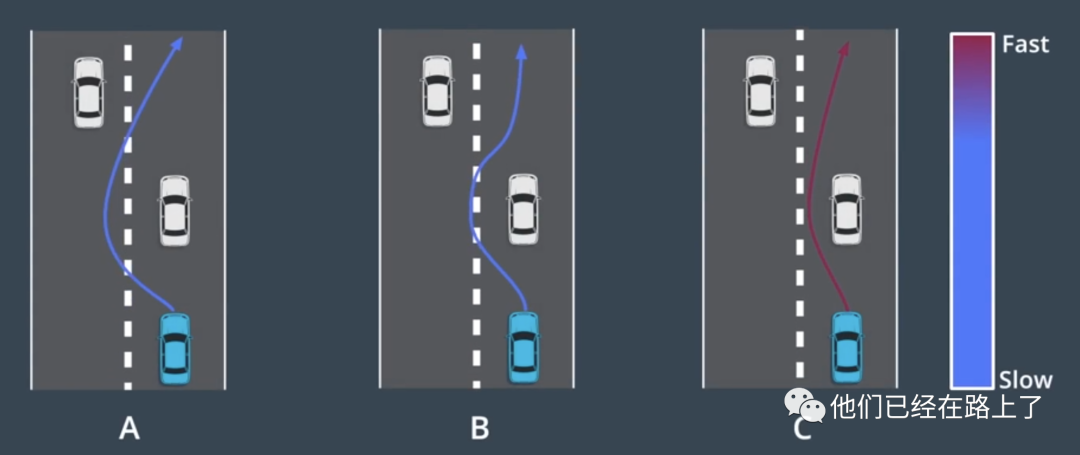
那我们如何选择一个最优轨迹呢?
这里就要使用“成本函数”。
成本函数为每一个轨迹分配了一个“成本”,轨迹成本由各种犯规处罚组成,例如偏离道路中心、有可能会碰撞、超出速度限制、轨迹的曲率和加速度会让乘客感觉到不舒服,这些均会让成本增加,轨迹成本将所有这些缺陷聚合为单个数字,这让我们可以对不同的轨迹进行排名,车辆甚至可能在不同的环境中使用不同的成本函数,例如高速公路的成本函数可能就与停车场的成本函数不同。
3.3 更适合自动驾驶的坐标系
我们通常使用笛卡尔坐标系描述物体的位置,也就是我们常说的直角坐标系,但是笛卡尔坐标系对自动驾驶而言并不是最佳选择,这是因为我们即便得到了车辆的x、y值,但是如果没有搭配地图的话,我们很难判断车辆究竟在什么位置或车辆行驶了多远,例如车辆是否在车道线的中间,是否压车道线等。因此一个更好的坐标系——Frenet坐标系就成了必然的选择。
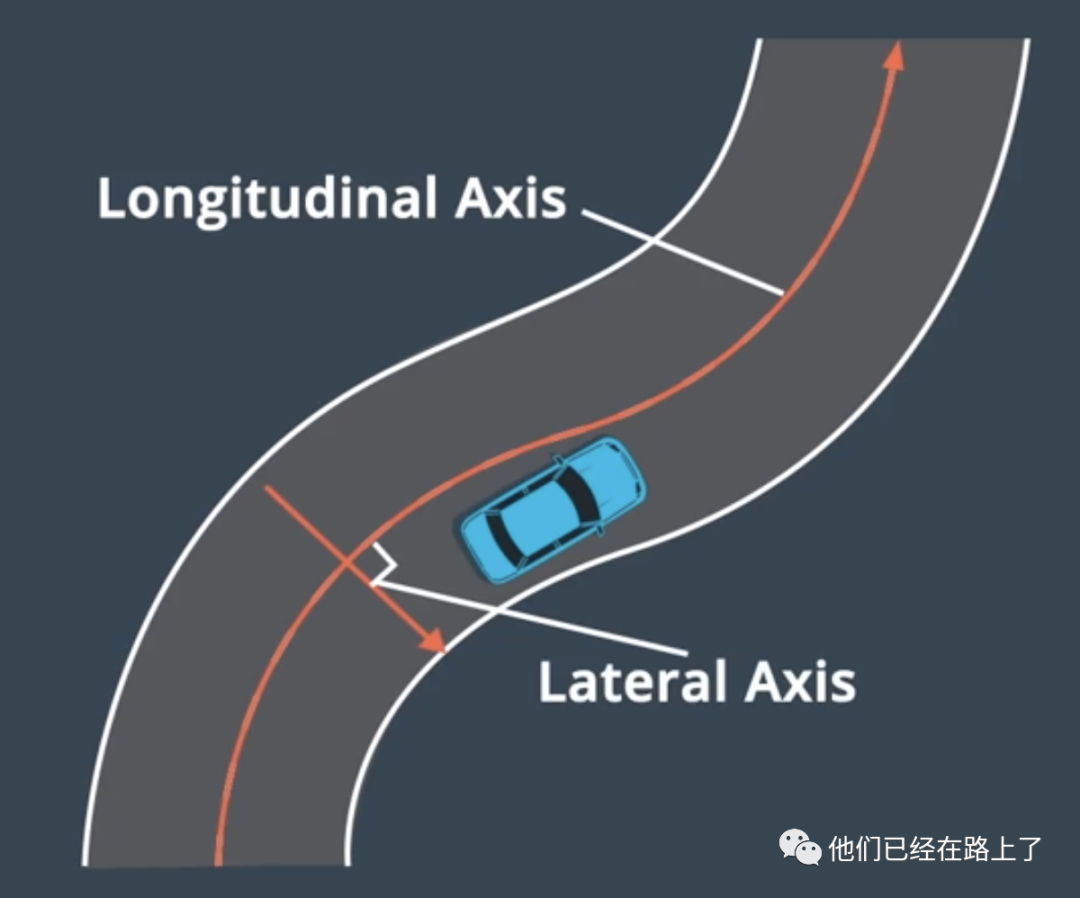
Frenrt坐标系描述了汽车相对于道路的位置,在Frenet框架中,s代表沿着道路的距离,也被称为纵坐标,d表示与纵向线的位移,也被称为纵坐标,在道路的每个点上,横轴和纵轴都是垂直的,纵坐标表示在道路中的行驶距离,横坐标表示汽车偏离中心线的距离。
3.4 轨迹规划=路径规划+速度规划
我们通常将轨迹规划分为两部分,来实现轨迹-速度的解耦:
路径规划
速度规划
在路径规划的步骤中,生成候选曲线,这是车辆可行驶的路径,我们使用成本函数对每条路径进行评估,该函数包括平滑度、安全性、与车道中心的偏离等,我们对得到的结果进行排名,选择成本最低的路径。
在速度规划的步骤中,我们可能希望改变在该路径上的速度,所以我们真正需要选择的是与路径点相关的一系列的速度,而不是一个单一的速度,我们将该序列称作“速度曲线”,我们可以使用优化功能给路径去选择受到各种限制的良好速度曲线,通过将路径和速度曲线相结合,可构建车辆行驶轨迹。
接下来我们就对这两个步骤展开介绍一下。
3.4.1 路径规划(轨迹的生成与选择)
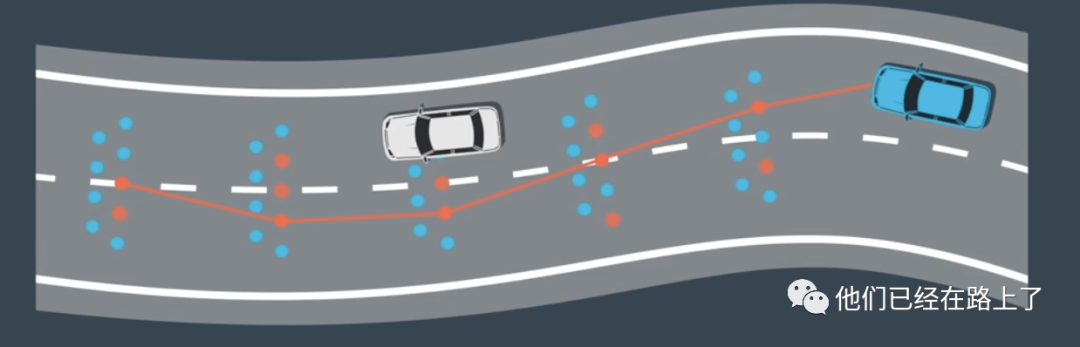
为了在轨迹-速度解耦规划中生成候选路径,我们首先将路段分割成单元格,然后对这些单元格中的点进行随机采样,通过对每个单元格中取一个点并将点连接,由此来创建了候选路径,通过重复此过程,我们可以构建多个候选路径,我们使用成本函数对路径进行评估,并选择最低成本的路径,成本函数可以考虑以下因素:
与车道中心的偏离
与障碍物的距离
速度和曲率的变化
对车辆的压力
以及我们希望加入考虑的任何其他因素
3.4.2 速度规划(速度的生成与选择)
在这个步骤中,我们采用一个叫“ST图”的工作来帮助我们设计和选择速度曲线,在ST图中,S表示车辆的纵向位移,t表示时间,ST图上的曲线是对车辆运动的描述,它说明了对车辆在不同时间的位置,由于速度是位置变化的速率,我们可以通过查看曲线的斜率从ST图上推断速度,斜率越大,也就是斜坡越陡,代表速度越快。
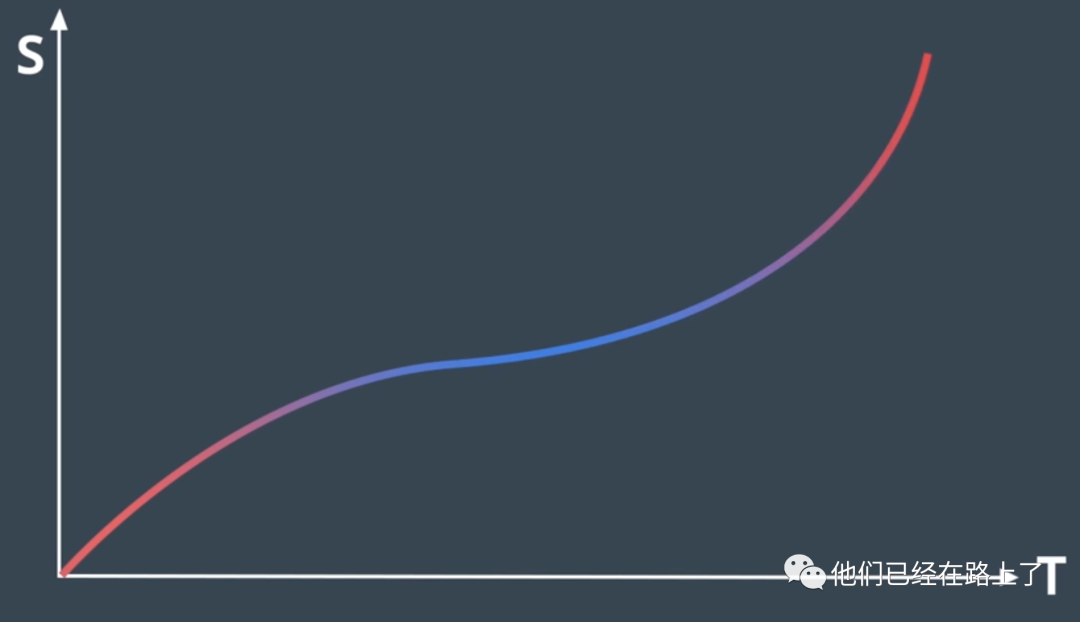
接下来,我们需要将ST图离散为多个单元格:
单元格之间的速度有所变化,但在每个单元格内,速度保持不变,该方法可以简化速度曲线的构建,并维持曲线的近似度。在ST图中,可以将障碍物绘制在特定时间段内,来阻挡道路的某些部分的矩形,例如,假设预测模块预测车辆将在t0到t1的时间段内驶入我们的车道,由于该车将在此期间占据s0到s1的位置,因此我们在ST图上绘制了一个矩形:
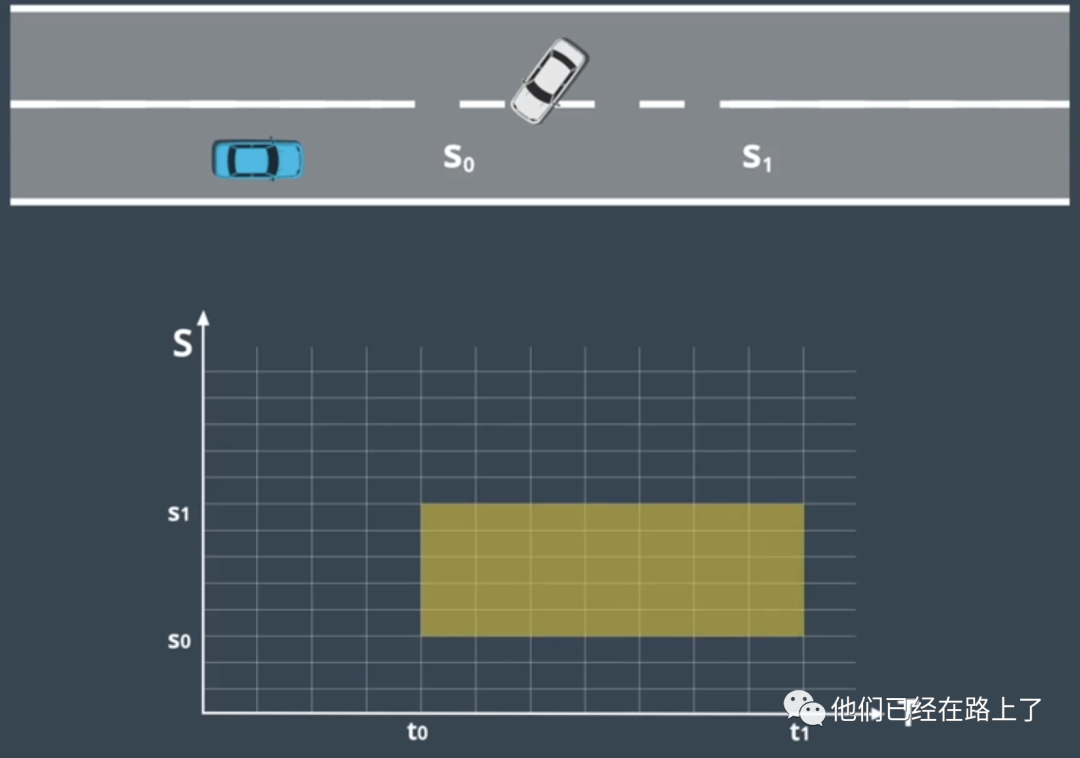
此时,速度曲线就不能与该矩形框相交,既然有了一张各种单元格被阻挡的ST图,我们就可以使用优化引擎为该图选择最佳的速度曲线:

优化算法通过复杂的数学运算来搜索,他会受到各种限制的低成本解决方案,这些限制同样会包含:
法律限制
距离限制
汽车物理限制
以及更多
3.4.3 二次规划对轨迹进行优化
接下来我们说说对路径-速度解耦结果的优化。
路径-速度解耦规划在很大程度上取决于离散化,所谓离散,我们在前面提到过两次,一次是对道路分割为单元格,选择单元格内的点连接起来,这是为了选择路径,另一次是将速度曲线分成离散的方格,用来选择速度。尽管离散让这些问题更容易被解决,但是这种解决方案的轨迹并不平滑,为了将离散解决方案转化为平滑的轨迹,这时候我们可以选择“二次规划”技术,二次规划将平滑的非线性曲线与这些分段式的线拟合:
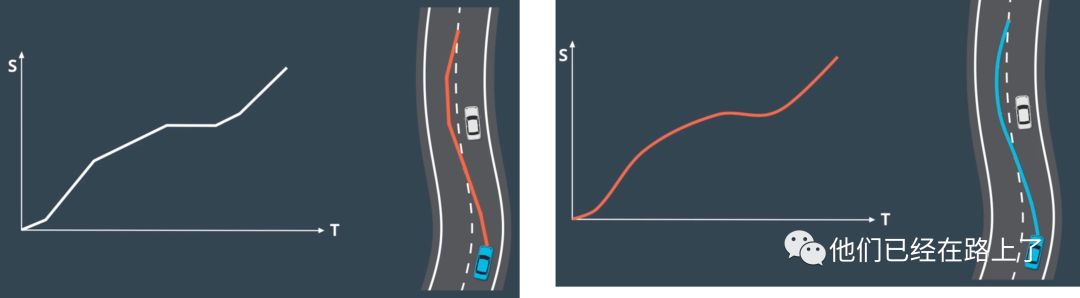
尽管二次规划背后的数学运算很复杂,但对我们的目的而言,细节并不是必须的,我们只需要简单使用几种不同的优化包中的一种即可。
一旦路径和速度曲线就绪,我们就可以将他们合并,构建出三维轨迹了。
3.5 回顾一下
到了这里我们已经生成了轨迹了,我们再来回顾一下整个流程: 假如我们正在路上行驶,我们感知到了我们正在逐步靠近一辆缓慢行驶的白色小车:
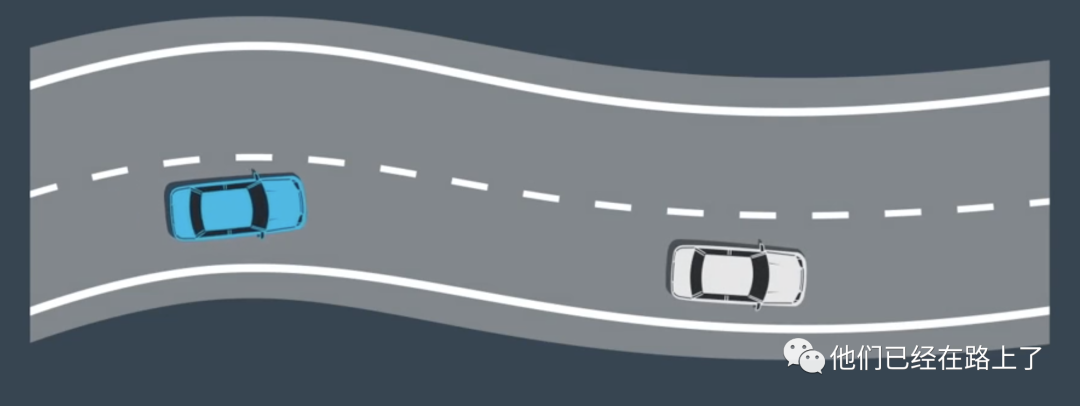
我们在这辆车的周围生成多条候选路线;
使用成本函数对候选路径进行评估并选择最优路线;
然后使用ST图进行速度规划;
我们根据其他车辆随时间变化的位置阻挡ST图的部分区域;
优化引擎帮助我们确认最优速度曲线;
使用二次规划让路径和速度曲线变的平滑;
最后我们将路径和速度曲线合并构建成轨迹;
今天的介绍就到这里,目前我们已经实现了路径规划和轨迹规划,下一节我们就来看看无人驾驶的控制功能。
