3D相机技术 | 立体视觉传感器+TOF相机

1. 前言

2. 立体视觉传感器原理简介

3. 工业领域应用

4. 主流立体视觉的产品

5. TOF相机工作原理

6. TOF工业领域应用

7. 一些TOF研究机构

立体传感器使用的原理与HVS相同:用两台摄像机从不同的位置观察场景，为了能够正确的重建运动物体，相机的同步是至关重要的。好比人的双眼同时观看，很难想象，不同步会看到什么。

相机的不同视点导致了与相机一定距离的点在两幅图像中的不同位置，这就产生了视差。视差是实现场景中点的三维重建的基本信息。（如何亲测视差？将一根手指放在眼前，切换左右眼，发现每只眼睛看到的位置是不一样的）

为了能够进行三维重建，相机必须进行标定，并确定其相对方位，标定通常由传感器制造商执行。标定数据使立体传感器能够对三维点进行三角测量。三角形的已知边是立体系统的基线，也就是连接两台摄像机的两个投影中心(入口瞳孔)的线段。此外，一旦知道两个摄像机的内部方位，摄像机本质上就是角度测量装置。因此，如果在这两幅图像中的某点都被识别出对应于场景中的同一点，那么光线到这一点的角度就可以计算出来。描述三维重建的等价方法如下:一旦在图像中识别出对应的点，就可以计算出它们在空间中的光线。重建后的三维点由两束光的交点确定。

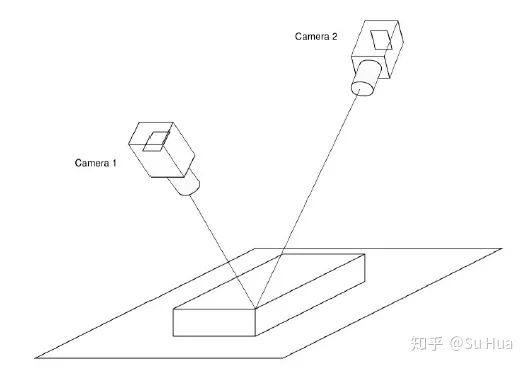
注意，场景中的某些点可能在一个或两个摄像机的视角被遮挡。例如，在图1)中，矩形长方体底边周围的所有点至少被一个摄像机遮挡。显然，这些点的三维位置无法重建。这个问题发生在所有基于三角测量的传感器上。

对应的点通常通过匹配两图像中一个小矩形窗口来确定的。也可以通过特征点进行匹配。不管是哪种，图像都必须包含足够数量的结构或纹理。否则，无法唯一地确定对应的点。由于很多工业物体都是无纹理的，所以在场景中使用随机纹理。投影仪通常安装在摄像机之间，在场景中投射一个静态模式，也可以在场景中投射多个随机模式。为了在深度不连续时能获取更精确的三维重建结果，可以减少匹配窗口大小，甚至可以减少到1*1，这将在深度不连续处得到非常精确的三维重建，不过同时计算量也是非常大的。使用多个模式的一个缺点是对象不能移动。

立体传感器大多是基于面阵相机的，也可以使用线扫描相机进行立体重建。立体线传感器可以实现非常高分辨率的三维重建。但要求物体必须相对于传感器移动才能进行三维重建。

主要应用在无人驾驶、立体视频、虚拟现实、三维跟踪、移动机器人、医疗机器人等多个领域。

比较知名的产品有

1）STEROLABS 推出的ZED 2K Stereo Camera

它有很高的分辨率和帧率

可以感知室内/室外0.5~20m是深度范围

2）Point Grey 公司推出的 BumbleBee

Bumblebee 系列利用双目立体匹配计算，可实时得到场景深度信息和三维模型, 可以快速构建立体视频及立体重目 目前包括有双目和三目两类，实时3D数据转换，每秒产生100万个3D点。

它的分辨率不如上面那款高

CWM飞行时间相机

CWM TOF相机发射辐射，通常在近红外范围，即振幅调制为一定频率fm的正弦波，在15到30兆赫之间，辐射被场景中的物体反射并被相机接收，相机在一个调制辐射的周期内测量四次反射辐射的量，这将创建测量mi, i = 0, … , 3, 间隔的时间间隔为π/ 2的接收波。发射波和接收波之间的相移可以解调如下：

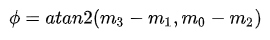
 表示双参数的反正切函数,它返回的结果是[0,2π)。此外，这四个测量值可以用来计算场景强度

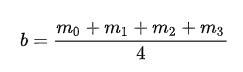
和幅值

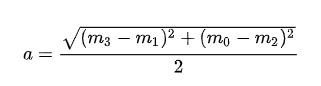
可以用来预测测量的质量。在传感器的集成时间(曝光时间)内进行多次测量，以提高信噪比。

该相位在所谓的无歧义距离范围内是唯一的：

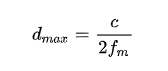
其中 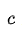 是光速，举个例子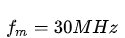，  ,则 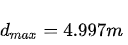 . 如果场景中存在距离大于  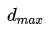的物体，则相位将出现折回干扰。这样一来，必须使用相位展开算法，这是非常耗时的，几乎从未使用过。因此，对于距离大于  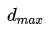的对象，将返回一个错误的对象距离。

如果对象距离d在无歧义范围内，则可计算为：

CWM TOF相机会发生系统和随机的错误。例如,距离测量可能依赖于积分时间,这可能会导致错误1到10厘米,相机内部的散射辐射会导致相对较大的距离误差,因为距离的测量可能取决于场景中的物体的反射,故可能存在系统的深度失真(摆动)，因为发射的辐射并不完全是正弦波。

CWM TOF相机可以有高达30HZ的高帧率。然而，它们的缺点之一是相对较小的分辨率:大多数商用传感器的分辨率低于320X240像素。

PM 飞行时间相机

PM TOF相机发射辐射脉冲，通常在近红外范围内，直接或间接测量辐射脉冲从辐射源到目标再返回传感器的飞行时间。让这个往返时间称为  。然后，相机到物体的距离为：

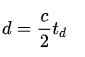
虽然  的直接测量在原则上是可行的，但在PM TOF相机中，往返时间是通过测量传感器接收到的辐射强度间接推断出来的。

一种基于  间接测量的PM TOF相机，其工作原理是发射一定持续时间  的辐射脉冲，如 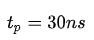 。脉冲持续时间决定了可以测量的最大目标距离(距离范围)

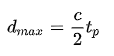
例如，对于 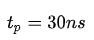 ，最大距离为4.497 m。在三个积分周期内测量返回到传感器的辐射。第一积分周期与辐射脉冲的发射同步。在三个积分周期内测量返回到传感器的辐射。第二个集成周期紧跟着第一个集成周期。这两个积分周期测量的是场景中物体反射的相机辐射强度。这两个测量值是用来推断场景中物体距离的主要数据。第三个积分周期发生在辐射脉冲发射前或发射后足够长的时间。其目的是对场景中物体反射的环境辐射效应的距离测量进行校正。

我们检查前两个积分周期，并假设场景中没有环境辐射反射。在第一个集成期间，靠近相机的物体反射的辐射会对传感器上的电荷产生很大的贡献。物体离传感器越近，相机上的电荷就越高。另一方面，在第二次积分期间，距离相机较远的物体反射的辐射对传感器的电荷有很大的贡献。物体离传感器越远，相机上的电荷就越高。

例如，在d = 0处的物体在第一个积分周期内只产生一个电荷，而在第二个积分周期内由于在第一个集成期间，整个辐射脉冲返回到传感器而不产生电荷。另一方面，d = dmax处的物体在第二次积分期间只会产生一个电荷，因为在第一次积分期间脉冲无法返回传感器。最后一个例子是，在d = dmax/2处的物体在第一个和第二个积分期间会产生相等的电荷。这说明td的飞行时间可以从传感器上的电荷推断出来，让前两个积分周期的电荷分别用q1和q2表示。然后，可以证明

注意，对于距离大于dmax的对象，在本例中，q1 = 0，因此降为td = tp。这就是为什么距离大于dmax的物体无法被正确测量的原因。

上式假设没有环境辐射。这在实践中很少是真的。第三个积分周期可用于校正环境辐射效应的深度测量。

让第三个积分周期产生的电荷记为q3。然后，q3可以从q1和q2中减去，抵消环境辐射，得到：

因此，场景中某点的距离

上述测量在传感器的曝光时间内进行多次，以提高信噪比。

目前还不存在对PMTOF相机的系统和随机错误影响的全面分析。我们可以假设已知的对CWM TOF相机存在影响的因素也会影响PMTOF相机。

例如，我们知道PM TOF相机会受到依赖于场景中物体反射率的深度偏差的影响。PM TOF相机的时间噪声可以达到几厘米级。

PM TOF相机支持高帧率(高达30赫兹)。此外，它们提供比CWM TOF相机更高的分辨率。目前市面上出售的PM TOF相机的分辨率从320×240到1280×1024像素不等。

与立体相机或三角测量系统比，TOF相机体积小巧，跟一般相机大小相去无几，非常适合于一些需要轻便、小体积相机的场合。TOF相机能够实时快速的计算深度信息，达到几十到100fps；而双目立体相机需要用到复杂的相关性算法，处理速度较慢。TOF的深度计算不受物体表面灰度和特征影响，可以非常准确的进行三维探测；而双目立体相机则需要目标具有良好的特征变化，否则会无法进行深度计算。

TOF的深度计算精度不随距离改变而变化，基本能稳定在cm级，这对于一些大范围运动的应用场合非常有意义，这些优势都使得它更易在工业上的推广。

TOF 相机目前的主要应用领域包括：

物流行业：通过 TOF 相机迅速获得包裹的抛重（即体积），来优化装箱和进行运费评估；

安防和监控：
进行 Peoplecounting 确定进入人数不超过上限；
通过对人流或复杂交通系统的counting，实现对安防系统的统计分析设计；
敏感地区的检测对象监视；

机器视觉：

工业定位、工业引导和体积预估；
替代工位上占用大量空间的、基于红外光进行安全生产控制的设备。