综述 | 相机标定方法
点击上方“小白学视觉”,选择加"星标"或“置顶”
重磅干货,第一时间送达
在图像测量过程以及机器视觉应用中,为确定空间物体表面某点的三维几何位置与其在图像中对应点之间的相互关系,必须建立相机成像的几何模型,这些几何模型参数就是相机参数。在大多数条件下这些参数(内参、外参、畸变参数)必须通过实验与计算才能得到,这个求解参数的过程就称之为相机标定(或摄像机标定)。无论是在图像测量或者机器视觉应用中,相机参数的标定都是非常关键的环节,其标定结果的精度及算法的稳定性直接影响相机工作产生结果的准确性。因此,做好相机标定是做好后续工作的前提,提高标定精度是科研工作的重点所在。
标定的目的主要为解决两个问题:
a、确定世界坐标系下三维空间点与像素平面像素点间的转换关系(内外参);
b、确定相机成像过程中的畸变系,用于图像矫正。
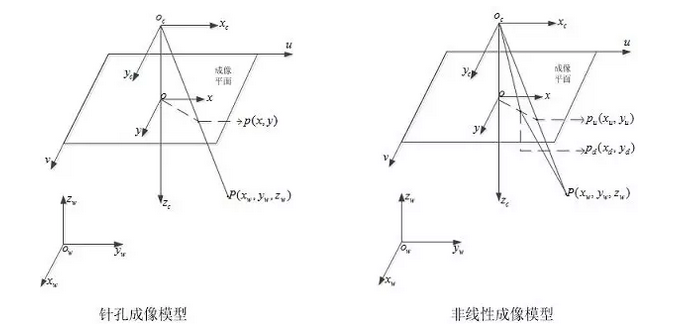
相机将三维世界中的坐标点(单位:米)映射到二维图像平面(单位:像素)的过程能够用一个几何模型来描述,其中最简单的称为针孔相机模型 (pinhole camera model),其框架如下图所示:
其中,涉及到相机标定涉及到了四大坐标系,分别为:
像素坐标系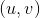 :为了描述物体成像后的像点在数字图像上(相片)的坐标而引入,是我们真正从相机内读取到的信息所在的坐标系。单位为个(像素数目)。
:为了描述物体成像后的像点在数字图像上(相片)的坐标而引入,是我们真正从相机内读取到的信息所在的坐标系。单位为个(像素数目)。
成像平面坐标系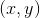 :为了描述成像过程中物体从相机坐标系到图像坐标系的投影透射关系而引入,方便进一步得到像素坐标系下的坐标。单位为m。
:为了描述成像过程中物体从相机坐标系到图像坐标系的投影透射关系而引入,方便进一步得到像素坐标系下的坐标。单位为m。
相机坐标系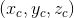 :在相机上建立的坐标系,为了从相机的角度描述物体位置而定义,作为沟通世界坐标系和图像/像素坐标系的中间一环。单位为m。
:在相机上建立的坐标系,为了从相机的角度描述物体位置而定义,作为沟通世界坐标系和图像/像素坐标系的中间一环。单位为m。
世界坐标系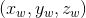 :用户定义的三维世界的坐标系,为了描述目标物在真实世界里的位置而被引入。单位为m。
:用户定义的三维世界的坐标系,为了描述目标物在真实世界里的位置而被引入。单位为m。
下面,我们来详细推导从世界坐标系到像素坐标的过程。
从世界坐标系到相机坐标系, 这是一个刚体变换,只需对世界坐标系的三维点作用一个旋转R和平移t(R,t即为相机的外参),变换过程可以通过一下公式完成:
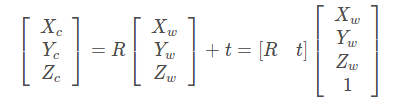
这一过程进行了从三维坐标到二维坐标的转换,也即投影透视过程(用中心投影法将物体投射到投影面上,从而获得的一种较为接近视觉效果的单面投影图,也就是使我们人眼看到景物近大远小的一种成像方式)。
成像过程如下图所示:针孔面(相机坐标系)在图像平面(图像坐标系)和物点平面(棋盘平面)之间,所成图像为倒立实像。
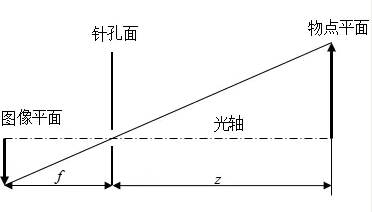
但是为了在数学上更方便描述,我们将相机坐标系和图像坐标系位置对调,变成下图所示的布置方式(没有实际的物理意义,只是方便计算):
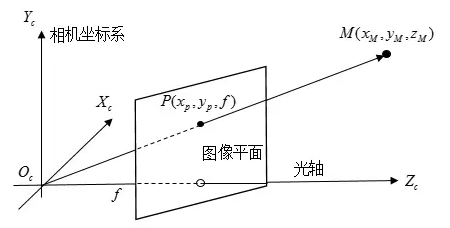
此时,假设相机坐标系中有一点M,则在理想图像坐标系下(无畸变)的成像点P的坐标为(可由相似三角形原则得出):
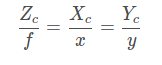
f为焦距,整理,得:
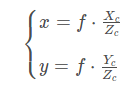
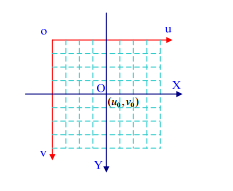
如上图,成平面坐标系和像素坐标系之间存在一个缩放和平移
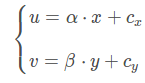
整理得:
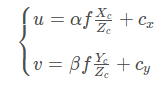
以fx、fy的方式表示为:
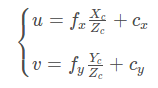
其中
α、β的单位为像素/米;
fx、fy为x、y方向的焦距,单位为像素;
(cx,cy)为主点,图像的中心,单位为像素。
那么,相机坐标系到像素坐标系的最终形式可写成:
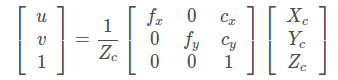
将 Zc移到左边:
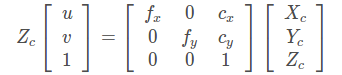
所以,在世界坐标系中的三维点M=[X,Y,Z]T 和像素坐标系中二维点m=[u,v]T的关系为:
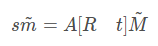
即:
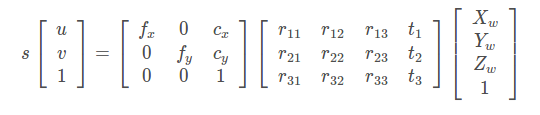
其中,s为缩放因子,A为相机的内参矩阵,[R t]为相机的外参矩阵,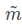 和
和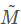 分别为m和M对应的齐次坐标。
分别为m和M对应的齐次坐标。
我们在摄像机坐标系到图像坐标系变换时谈到透视投影。摄像机拍照时通过透镜把实物投影到像平面上,但是透镜由于制造精度以及组装工艺的偏差会引入畸变,导致原始图像的失真。因此我们需要考虑成像畸变的问题。
透镜的畸变主要分为径向畸变和切向畸变,还有薄透镜畸变等等,但都没有径向和切向畸变影响显著,所以我们在这里只考虑径向和切向畸变。
径向畸变
顾名思义,径向畸变就是沿着透镜半径方向分布的畸变,产生原因是光线在原理透镜中心的地方比靠近中心的地方更加弯曲,这种畸变在普通廉价的镜头中表现更加明显,径向畸变主要包括桶形畸变和枕形畸变两种。以下分别是枕形和桶形畸变示意图:
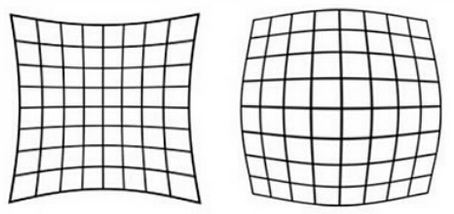
实际情况中我们常用r=0处的泰勒级数展开的前几项来近似描述径向畸变,矫正径向畸变前后的坐标关系为:
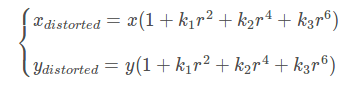
切向畸变
切向畸变是由于透镜本身与相机传感器平面(像平面)或图像平面不平行而产生的,这种情况多是由于透镜被粘贴到镜头模组上的安装偏差导致。畸变模型可以用两个额外的参数p1和p2来描述:
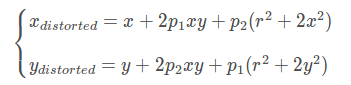
其中,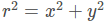
所以,我们一共需要5个畸变参数(k1,k2,k3,p1,p2)来描述透镜畸变。
综上所述,相机标定实际上就是确定相机的内外参数、畸变参数的过程。
以上是对于单个相机进行标定,那么对于多目相机系统或者RGBD 相机的标定呢?
对于多目相机系统或者RGBD 相机除了要对别对每个相机进行以上标定以外,还需要求传感器之间的变换T,以使同一时刻获取的数据能够“对齐”,以双目为例,左右两个相机的坐标系如下图:
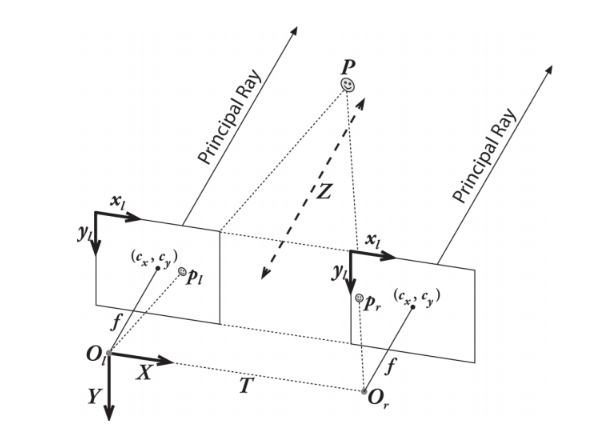
计算出两个摄像机之间的旋转矩阵R和平移向量t,方法是分别计算出两个摄像机的R和T,再由以下公式计算:
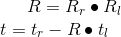
由于单相机获取的图像只能计算出二维坐标,因为我们使用了2套相机,且2套相机之间的关系也是已知的,那么如果我们能把三维空间中某点在左右相机成像的二维坐标都计算出来,且能知道这是同一个点,这样就可以计算出三维坐标。这里面确认同名点的技术就是立体匹配。立体匹配有很多种算法,其中局部匹配法是最常用的,但是就目前已有算法来说,没有一种算法可以实现100%匹配。一般来说待匹配点越多,匹配准确率越低。
相机标定方法有:传统相机标定法、主动视觉相机标定法、相机自标定法。
| 标定方法 | 优点 | 缺点 | 常用方法 |
|---|---|---|---|
| 传统相机标定法 | 可使用于任意的相机模型、 精度高 | 需要标定物、算法复杂 | Tsai两步法、张氏标定法 |
| 主动视觉相机标定法 | 不需要标定物、算法简单、鲁棒性高 | 成本高、设备昂贵 | 主动系统控制相机做特定运动 |
| 相机自标定法 | 灵活性强、可在线标定 | 精度低、鲁棒性差 | 分层逐步标定、基于Kruppa方程 |
(左右滑动查看)
Tsai两步法是先线性求得相机参数,之后考虑畸变因素,得到初始的参数值,通过非线性优化得到最终的相机参数。Tsai两步法速度较快,但仅考虑径向畸变,当相机畸变严重时,该方法不适用。
张氏标定法使用二维方格组成的标定板进行标定,采集标定板不同位姿图片,提取图片中角点像素坐标,通过单应矩阵计算出相机的内外参数初始值,利用非线性最小二乘法估计畸变系数,最后使用极大似然估计法优化参数。该方法操作简单,而且精度较高,可以满足大部分场合。
基于主动视觉的相机标定法是通过主动系统控制相机做特定运动,利用控制平台控制相机发生特定的移动拍摄多组图像,依据图像信息和已知位移变化来求解相机内外参数。这种标定方法需要配备精准的控制平台,因此成本较高。
分层逐步标定法是先对图像的序列做射影重建,在重建的基础上进行放射标定和欧式标定,通过非线性优化算法求得相机内外参数。由于初始参数是模糊值,优化算法收敛性不确定。
基于Kruppa的自标定法是通过二次曲线建立关于相机内参矩阵的约束方程,至少使用3对图像来标定相机。图像序列长度会影响标定算法的稳定性,无法保证射影空间中的无穷远平面。
以上为单个相机标定的方法,而对于相机-相机、相机-距离传感器之间进行标定,OpenCV、Matlab都有自带的工具箱或函数库可以用来标定,但[1]提出了一个带有Web界面的工具箱,用于全自动相机到相机和相机到范围的校准。该系统可在一分钟内恢复内外参数以及摄像机和距离传感器之间的转换。而且,该方法所提出的基于生长的棋盘格角点检测方法明显优于OpenCV需要指定棋盘格角点大小的角点检测方法。
交流群
欢迎加入公众号读者群一起和同行交流,目前有SLAM、三维视觉、传感器、自动驾驶、计算摄影、检测、分割、识别、医学影像、GAN、算法竞赛等微信群(以后会逐渐细分),请扫描下面微信号加群,备注:”昵称+学校/公司+研究方向“,例如:”张三 + 上海交大 + 视觉SLAM“。请按照格式备注,否则不予通过。添加成功后会根据研究方向邀请进入相关微信群。请勿在群内发送广告,否则会请出群,谢谢理解~

