神经网络之CNN与RNN的关系
点击下方卡片,关注“新机器视觉”公众号
视觉/图像重磅干货,第一时间送达
导读
本文主要是对CNN和RNN的理解,通过对比总结各自的优势,同时加深自己对这方面知识的理解,其中代码引用采用的是VQA模型中对图像和文本的处理。
1、CNN介绍
CNN是一种利用卷积计算的神经网络。它可以通过卷积计算将原像素很大的图片保留主要特征变成很小的像素图片。本文以李宏毅老师ppt内容展开具体介绍。
1.1 Why CNN for Image

①为什么引入CNN ?
图片示意:给定一个图片放入全连接神经网络,第一个hidden layer识别这张图片有没有绿色出现?有没有黄色出现?有没有斜的条纹?第二个hidden layer结合第一个hidden layer的输出实现更复杂的功能,例如:如图如果看到直线+横线就是框框一部分,如果看到棕色+条纹就是木纹,如果看到斜条纹+绿色就是灰色类条纹一部分。再根据第二个hidden layer输出结果,如果某个神经元看到蜂巢就会activate,某个神经元如果看到人就会activate。
但是我们如果一般地用fully network(全连接)神经网络处理的话,我们会需要很多的参数,例如如果input的vector是个30000维,第一个hidden layer假设是1000个神经元,那么第一个hidden layer就会30000*1000个,数据量非常大,导致计算效率和准确率效果低,而引入CNN,主要就是解决我们这些问题,简化我们神经网络架构。因为 某些weight我们是用不到的,CNN会使用过滤手段(filter)将一些不需要的参数过滤掉,保留一些重要的参数做图像处理。
②为什么使用比较少的参数就足够进行图像处理 ?
三个特性:
大部分的patterns要比整张图片小,一个神经元不需要去观察整个图片,只需要观察图片的一小部分就能找到一个想要的pattern,例如:给定一张图片,第一个hidden layer的某个神经元找图像中的鸟的嘴,另一个神经元找鸟的爪子。如下图只需要看红色框不需要观察整张图就可以找到鸟嘴。

不同位置的鸟嘴只需要训练一个识别鸟嘴的参数就Ok了,不需要分别训练。
我们可以采用子样品来使图片变小,子样不会改变目标图像。
1.2 CNN架构图
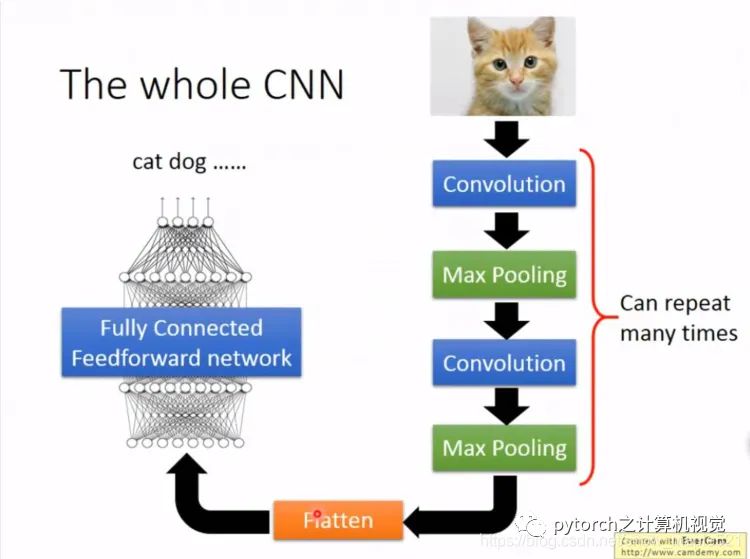
1.1节的前两个property需要卷积计算,后一个池化层处理,具体下节介绍。
1.3 卷积层
1.3.1 重要参数

1.3.2 卷积计算
矩阵卷积计算如下:
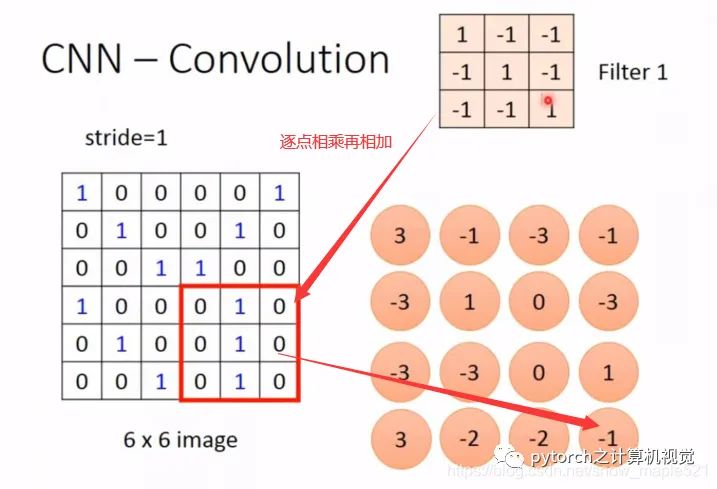
计算如下:图像传入的是553的像素值,经过padding=1的填充构成773的像素值,卷积核是333的大小,2个卷积核,步数stride=2。注意这里的卷积核深度要核传入过来的像素值深度相同,当每次扫描到的蓝色位置数对应卷积核红色位置数位置相乘后相加得到绿色位置的数据。
像素数变化为:(n+2p-f)\s = (5+2-3)\2 + 1= 3得到332的数据,经过卷积输出的像素深度等于上一层输入的卷积核数目。将得的结果作为池化层的输入值。
卷积核大小选取往往是奇数。深度要和它的上一层输出像素值深度相同,如动图卷积核的选取是3*3*3,而输出像素值深度=本次卷积的卷积核数。这点不要混淆。
1.3.3 卷积层与全连接层的关系
其实卷积就是将全连接层的一些weight拿掉,卷积层计算输出的结果,其实就是全连接层的hidden layer输出的结果。如下图所示:
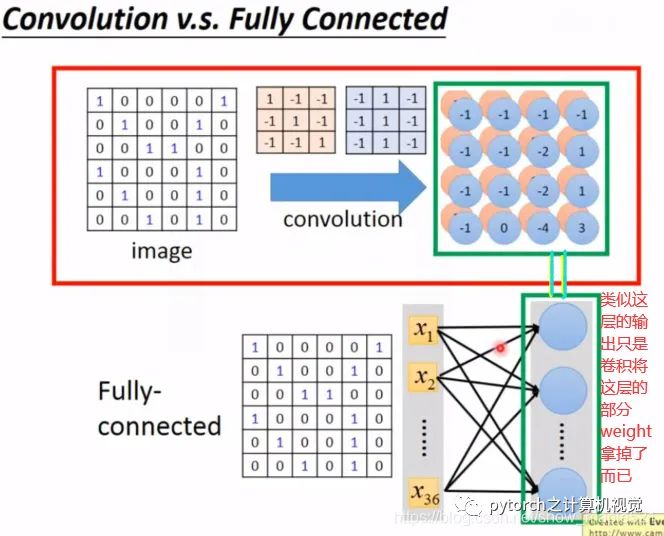
卷积没有考虑输入的全部特征,只和filter中经过的特征有关,如下:6*6的图像展开成36pixel,然后下一层只和输入层的9个pixel有关,没有连接全部,这样就会使用很少的参数,具体图解如下:

由上图也可发现,计算结果3和-1不像全连接网络那样全部都需要不同的weight,而这个3和-1的部分计算的weight相同,这就是所谓的参数共享(权值共享)
1.4 池化层
根据前一个卷积计算后的矩阵,再进行池化处理(将一个框框内的四个值合并一个值,可取最大值或者平均值),如下图:
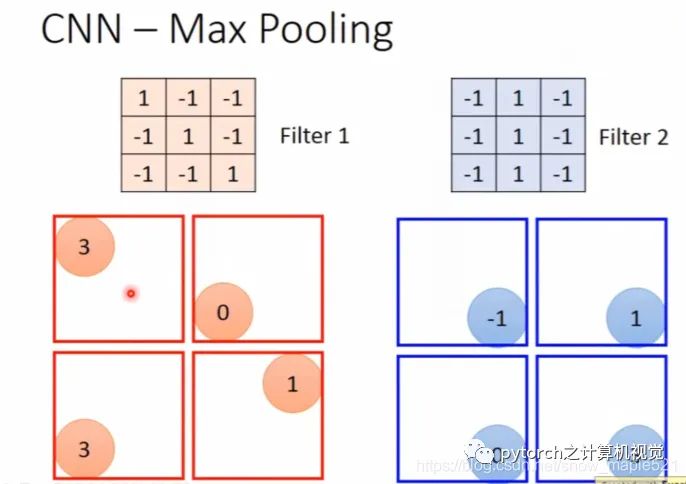
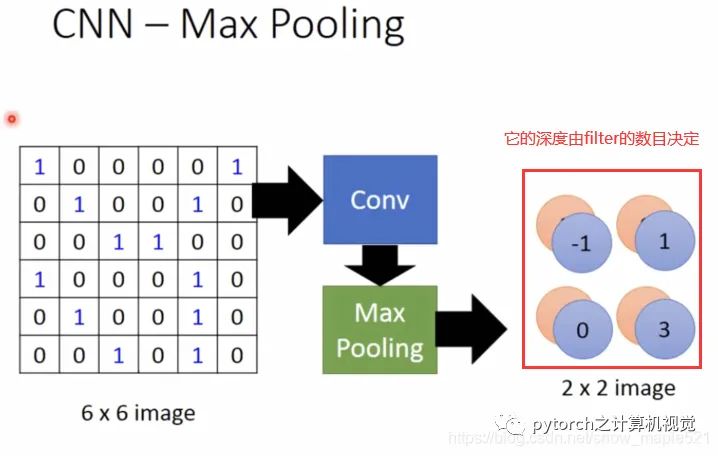
1.5 应用
主要使用pytorch框架来介绍卷积神经网络。
源代码:
torch.nn.Conv2d(
in_channels: int, #输入图像的通道数
out_channels: int, #卷积产生的输出通道数
kernel_size: Union[T, Tuple[T, T]], #卷积核大小
stride: Union[T, Tuple[T, T]] = 1, #卷积的步数 默认:1
padding: Union[T, Tuple[T, T]] = 0, #0填充添加到输入的两边 默认:0
dilation: Union[T, Tuple[T, T]] = 1, #核元素之间的间距 默认:1
groups: int = 1, #从输入通道到输出通道的阻塞链接数,默认:1
#groups:控制输入和输出之间的连接,输入和输出通道数必须被组整除,
#当groups=1:所有输入移交给所有输出
#当groups=2:相当于两个卷积层,一个看到一半的输入通道并产生一半的输出通道,将两个合并
#当groups=in_channels:每个通道都有自己的一组过滤器,其大小为out_channel/in_channel
bias: bool = True, #将可学习的偏差添加到输出中 默认:true
padding_mode: str = 'zeros')
#注:kenerl_size,stride,padding,dilation参数类型可以是int,可以是tuple,当是tuple时,第一个int是高度维度,第二个是宽度维度。当是单个int时,高度宽度值相同
# 方形核和等步幅
m = nn.Conv2d(16, 33, 3, stride=2)
# 非方形核和不等步幅和填充
m = nn.Conv2d(16, 33, (3, 5), stride=(2, 1), padding=(4, 2))
# 非方形核和不等步幅和填充和扩展
m = nn.Conv2d(16, 33, (3, 5), stride=(2, 1), padding=(4, 2), dilation=(3, 1))
input = torch.randn(20, 16, 50, 100)
output = m(input)
应用:此处采用的是VGG16,顺便介绍以下pytorch的torchsummary库,可以把网络模型打印出来,例如:
import torchvision.models as models
import torch.nn as nn
import torch
from torchsummary import summary
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
model = models.vgg16(pretrained=True).to(device)
print(model)
输出:
VGG(
(features): Sequential(
(0): Conv2d(3, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(1): ReLU(inplace)
(2): Conv2d(64, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(3): ReLU(inplace)
(4): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False)
(5): Conv2d(64, 128, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(6): ReLU(inplace)
(7): Conv2d(128, 128, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(8): ReLU(inplace)
(9): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False)
(10): Conv2d(128, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(11): ReLU(inplace)
(12): Conv2d(256, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(13): ReLU(inplace)
(14): Conv2d(256, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(15): ReLU(inplace)
(16): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False)
(17): Conv2d(256, 512, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(18): ReLU(inplace)
(19): Conv2d(512, 512, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(20): ReLU(inplace)
(21): Conv2d(512, 512, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(22): ReLU(inplace)
(23): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False)
(24): Conv2d(512, 512, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(25): ReLU(inplace)
(26): Conv2d(512, 512, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(27): ReLU(inplace)
(28): Conv2d(512, 512, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(29): ReLU(inplace)
(30): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False)
)
(classifier): Sequential(
(0): Linear(in_features=25088, out_features=4096, bias=True)
(1): ReLU(inplace)
(2): Dropout(p=0.5)
(3): Linear(in_features=4096, out_features=4096, bias=True)
(4): ReLU(inplace)
(5): Dropout(p=0.5)
(6): Linear(in_features=4096, out_features=1000, bias=True)
)
)
model.classifier = nn.Sequential(
*list(model.classifier.children())[:-1]) # remove last fc layer
print(model)
summary(model,(3,224,224))
输出:
----------------------------------------------------------------
Layer (type) Output Shape Param #
================================================================
Conv2d-1 [-1, 64, 224, 224] 1,792
ReLU-2 [-1, 64, 224, 224] 0
Conv2d-3 [-1, 64, 224, 224] 36,928
ReLU-4 [-1, 64, 224, 224] 0
MaxPool2d-5 [-1, 64, 112, 112] 0
Conv2d-6 [-1, 128, 112, 112] 73,856
ReLU-7 [-1, 128, 112, 112] 0
Conv2d-8 [-1, 128, 112, 112] 147,584
ReLU-9 [-1, 128, 112, 112] 0
MaxPool2d-10 [-1, 128, 56, 56] 0
Conv2d-11 [-1, 256, 56, 56] 295,168
ReLU-12 [-1, 256, 56, 56] 0
Conv2d-13 [-1, 256, 56, 56] 590,080
ReLU-14 [-1, 256, 56, 56] 0
Conv2d-15 [-1, 256, 56, 56] 590,080
ReLU-16 [-1, 256, 56, 56] 0
MaxPool2d-17 [-1, 256, 28, 28] 0
Conv2d-18 [-1, 512, 28, 28] 1,180,160
ReLU-19 [-1, 512, 28, 28] 0
Conv2d-20 [-1, 512, 28, 28] 2,359,808
ReLU-21 [-1, 512, 28, 28] 0
Conv2d-22 [-1, 512, 28, 28] 2,359,808
ReLU-23 [-1, 512, 28, 28] 0
MaxPool2d-24 [-1, 512, 14, 14] 0
Conv2d-25 [-1, 512, 14, 14] 2,359,808
ReLU-26 [-1, 512, 14, 14] 0
Conv2d-27 [-1, 512, 14, 14] 2,359,808
ReLU-28 [-1, 512, 14, 14] 0
Conv2d-29 [-1, 512, 14, 14] 2,359,808
ReLU-30 [-1, 512, 14, 14] 0
MaxPool2d-31 [-1, 512, 7, 7] 0
Linear-32 [-1, 4096] 102,764,544
ReLU-33 [-1, 4096] 0
Dropout-34 [-1, 4096] 0
Linear-35 [-1, 4096] 16,781,312
ReLU-36 [-1, 4096] 0
Dropout-37 [-1, 4096] 0
================================================================
Total params: 134,260,544
Trainable params: 134,260,544
Non-trainable params: 0
----------------------------------------------------------------
Input size (MB): 0.57
Forward/backward pass size (MB): 218.58
Params size (MB): 512.16
Estimated Total Size (MB): 731.32
----------------------------------------------------------------
2、RNN介绍
2.1 引言
每个订票系统都会有一个空位填充(slot filling),有些slot是Destination,有些slot是time of arrival,系统要知道哪些词属于哪个slot;例如:
I would like to arrive Taipei on November 2nd;
这里的Taipei就是Destination,November 2nd就是time of arrival;
采用普通的神经网络,将Taipei这个词丢入到网络中,当然在丢入之前要将其转化成向量表示,如何表示成向量?方法很多此处采用:1-of-N Encoding,表示方式如下:

其他词向量方式如下:
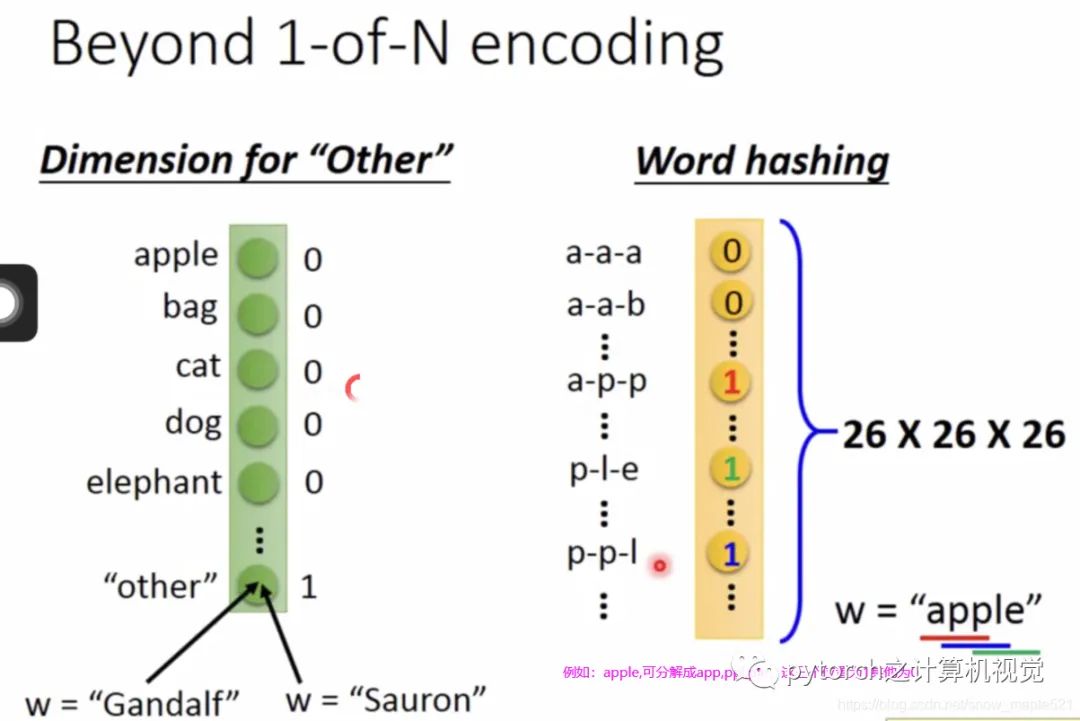
但是,如果有如下情况,系统就会出错。
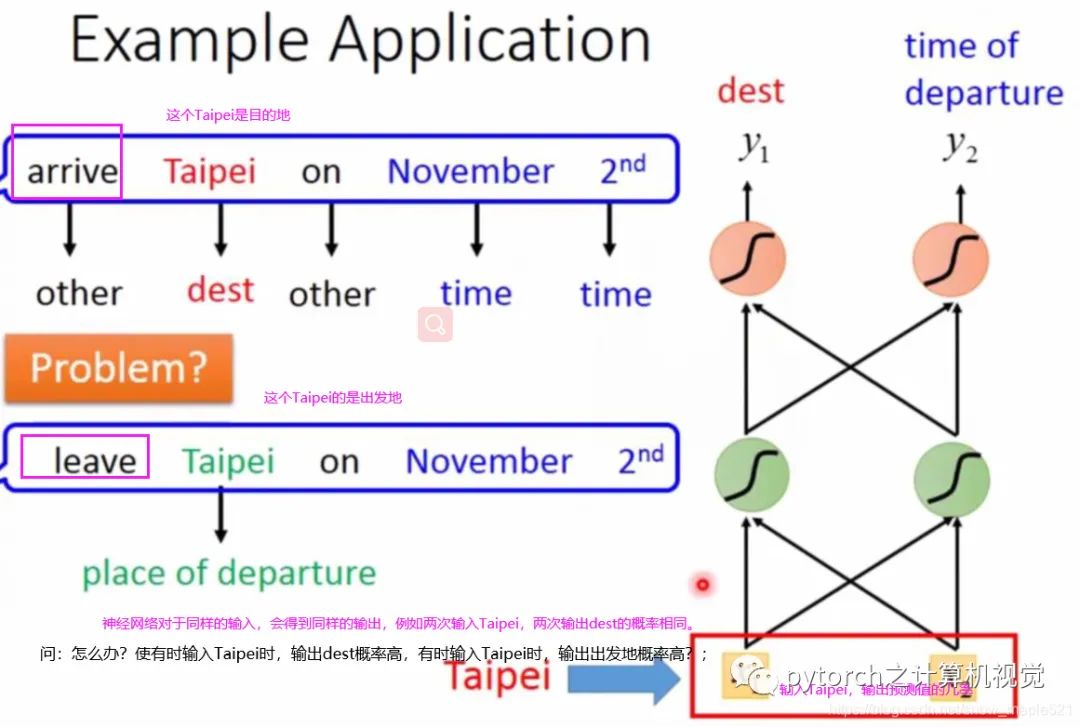
问: 怎么办?使有时输入Taipei时,输出dest概率高,有时输入Taipei时输出出发地概率高?
答: 此时就要使我们的网络有“记忆”,能记住前面输入的数据。例如:Taipei是目的地时看到了arrive,Taipei是出发地时看到了leave。那么这种有记忆的网络就叫做:Recurrent Neural Network(RNN)
2.2 RNN简介
RNN的隐藏层的输出会存储在内存中,当下次输入数据时会使用到内存中存储的上次的输出。图解如下:
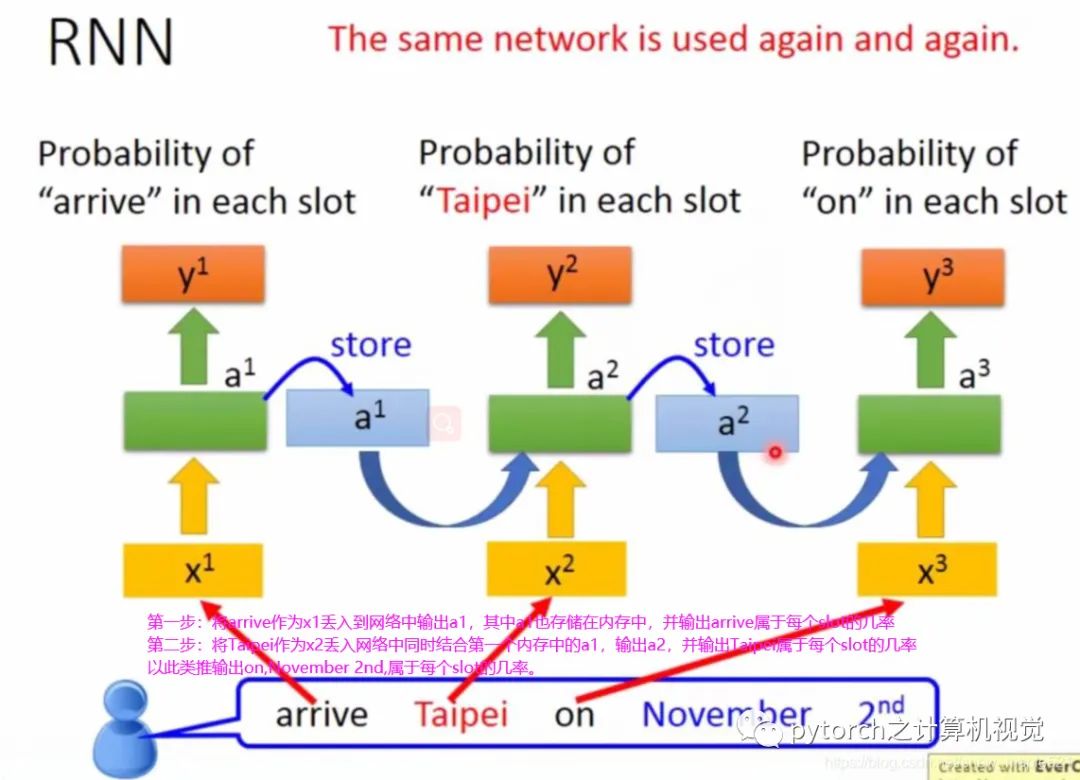
图中,同样的weight用同样的颜色表示。当然hidden layer可以有很多层;以上介绍的RNN是最简单的,接下来介绍加强版的LSTM;
2.3 RNN之LSTM
现在常用的内存(memory)是Long short-term内存。
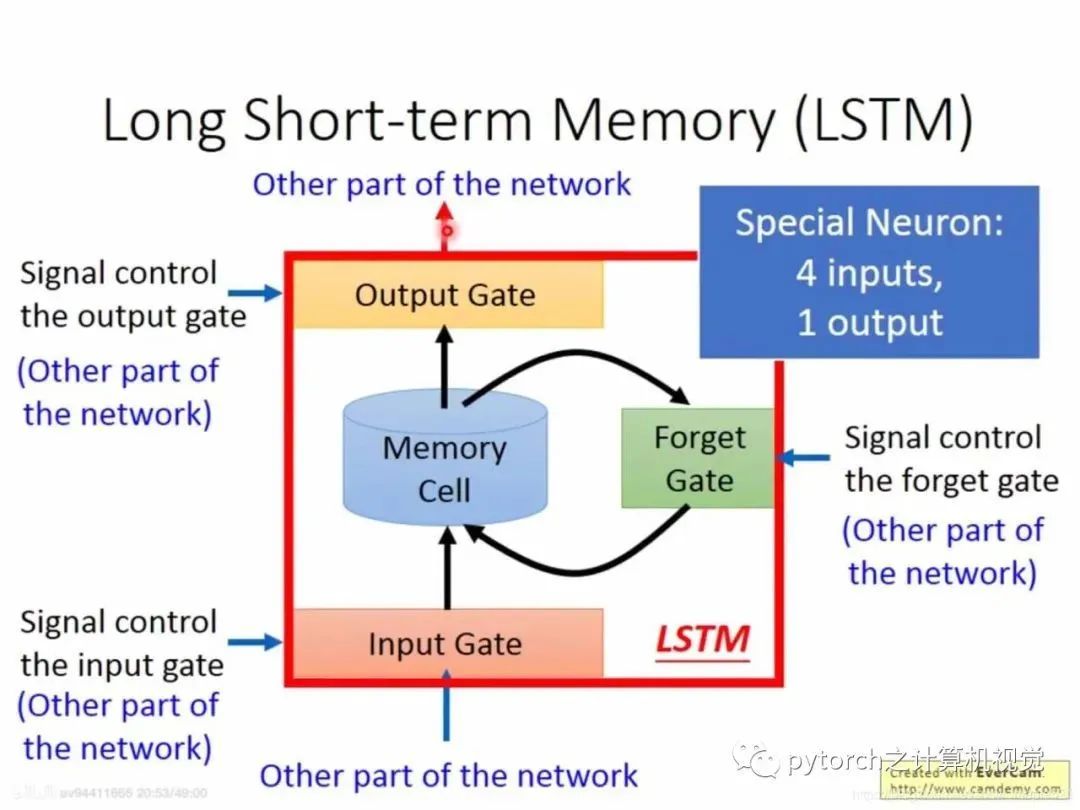
当外部信息需要输入到memory时需要一个“闸门”——input gate,而input gate什么时候打开和关闭是被神经网络学到的,同理output gate也是神经网络学习的,forget gate也是如此。
所以LSTM有四个input,1个output。简图如下:
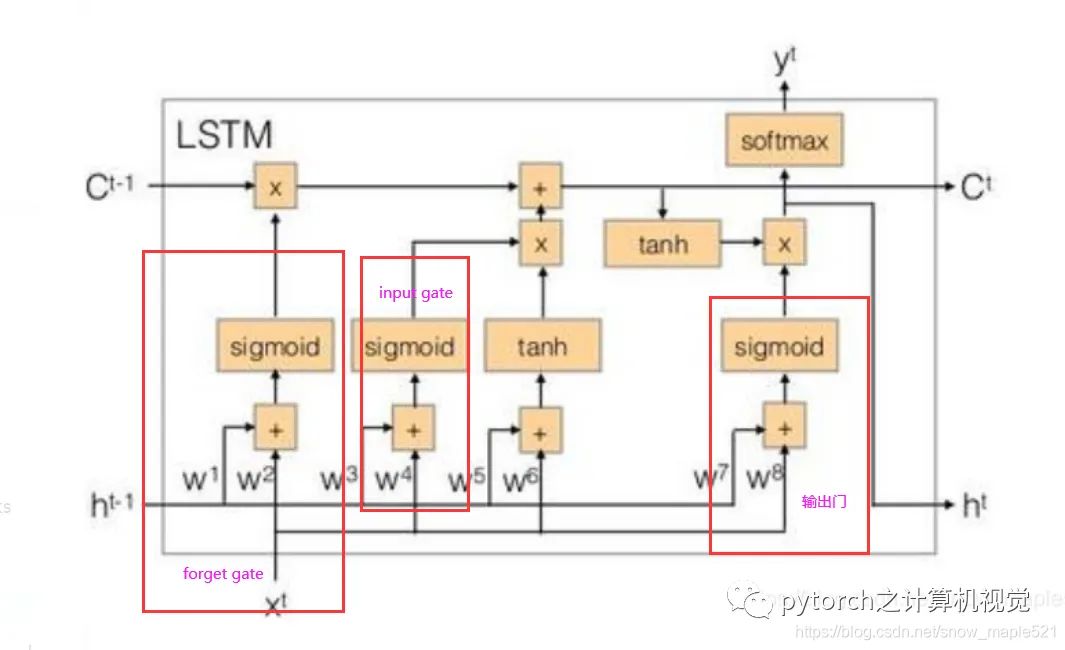
公式如下:
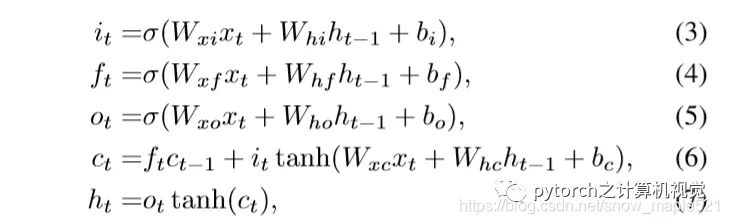
2.4 LSTM例子
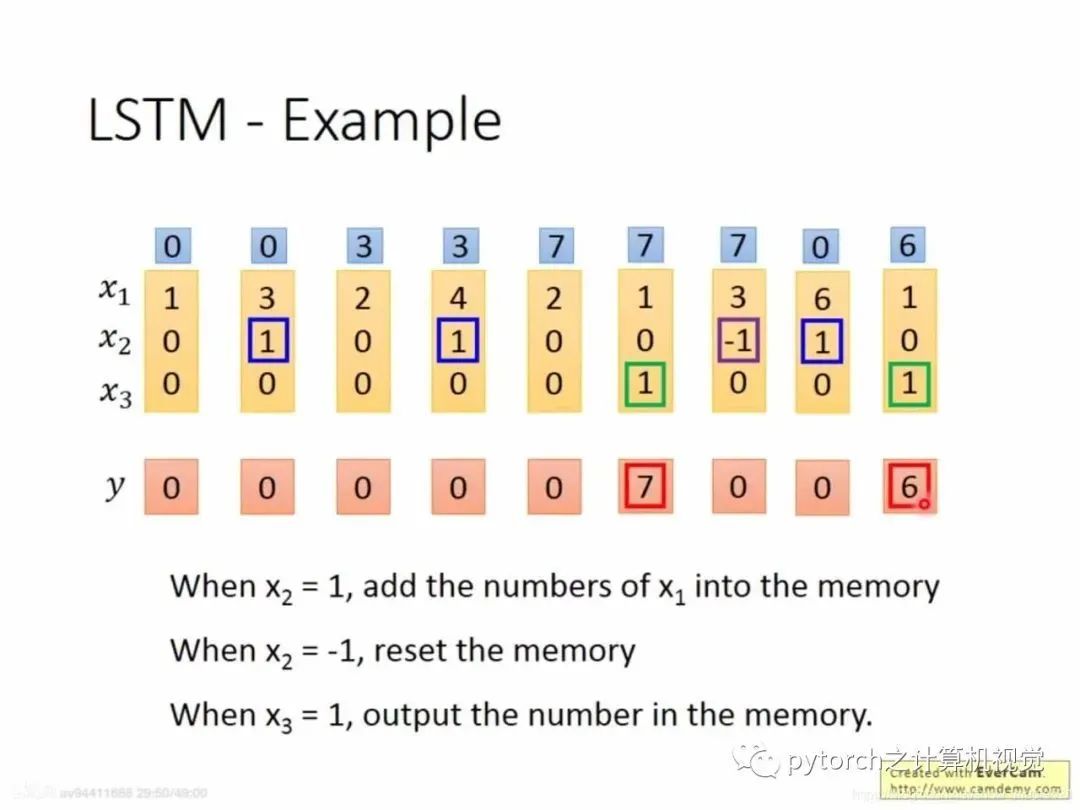
图中x2 = 1将x1送入memory中,如果x2=-1就清空memory的数值,如果x3=1,就将memory中的数据输出。如上图,第一列,x2=0不送入memory,第二列x2=1,将此刻x1=3送入memory中(注意memory中的数据是x1的累加,例如第四列,x2=1,此时有x1=4,memory中=3,所以一起就是7)第五列发现x3=1,可以输出,所以输出memory中的值7.
结合LSTM简图如下:
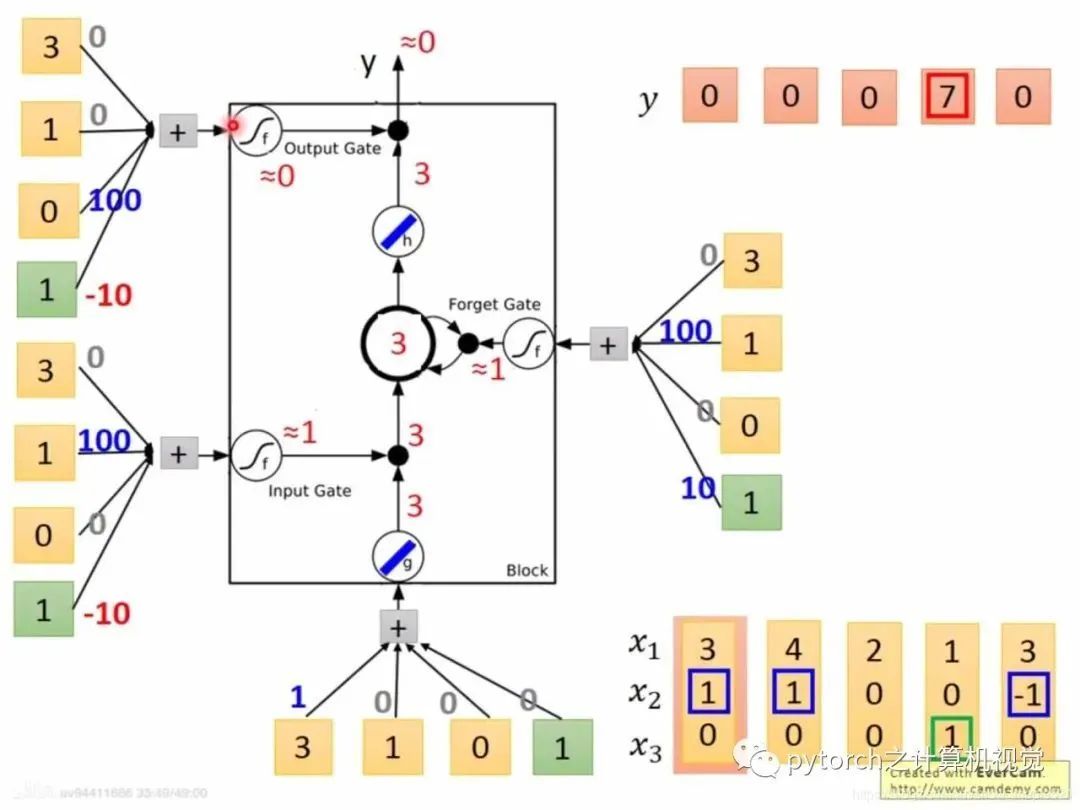
假设进来的是第一列:x1=3,x2=1,x3=0步骤:g—Tanh: x1w1+x2w2+x3w3 = 3f—sigmod: x1w1+x2w2+x3w3=90 sigmod后=1算好f和g后传入input gate=3*1=3,forget gate = 1,代表不需要清0,x3=0,代表output gate锁上,输出的还是0。
2.5 LSTM实战
pytorch中封装好了LSTM网络,直接采用nn.lstm即可使用,例如
class QstEncoder(nn.Module):
def __init__(self, qst_vocab_size, word_embed_size, embed_size, num_layers, hidden_size):
super(QstEncoder, self).__init__()
self.word2vec = nn.Embedding(qst_vocab_size, word_embed_size)
self.tanh = nn.Tanh()
self.lstm = nn.LSTM(word_embed_size, hidden_size, num_layers)
self.fc = nn.Linear(2*num_layers*hidden_size, embed_size) # 2 for hidden and cell states
def forward(self, question):
qst_vec = self.word2vec(question) # [batch_size, max_qst_length=30, word_embed_size=300]
qst_vec = self.tanh(qst_vec)
qst_vec = qst_vec.transpose(0, 1) # [max_qst_length=30, batch_size, word_embed_size=300]
_, (hidden, cell) = self.lstm(qst_vec) # [num_layers=2, batch_size, hidden_size=512]
qst_feature = torch.cat((hidden, cell), 2) # [num_layers=2, batch_size, 2*hidden_size=1024]
qst_feature = qst_feature.transpose(0, 1) # [batch_size, num_layers=2, 2*hidden_size=1024]
qst_feature = qst_feature.reshape(qst_feature.size()[0], -1) # [batch_size, 2*num_layers*hidden_size=2048]
qst_feature = self.tanh(qst_feature)
qst_feature = self.fc(qst_feature) # [batch_size, embed_size]
return qst_feature
3、CNN与RNN的区别
CNN与RNN区别链接如下,引用了这个博客作者总结,(https://blog.csdn.net/lff1208/article/details/77717149)具体如下。
DNN形成
为了克服梯度消失,ReLU、maxout等传输函数代替了sigmoid,形成了如今DNN的基本形式。结构跟多层感知机一样,如下图所示:
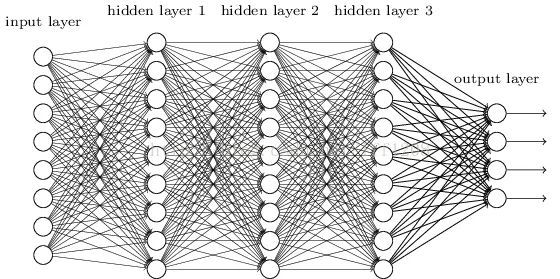
我们看到全连接DNN的结构里下层神经元和所有上层神经元都能够形成连接,从而导致参数数量膨胀。假设输入的是一幅像素为1K*1K的图像,隐含层有1M个节点,光这一层就有10^12个权重需要训练,这不仅容易过拟合,而且极容易陷入局部最优。
CNN形成
由于图像中存在固有的局部模式(如人脸中的眼睛、鼻子、嘴巴等),所以将图像处理和神将网络结合引出卷积神经网络CNN。CNN是通过卷积核将上下层进行链接,同一个卷积核在所有图像中是共享的,图像通过卷积操作后仍然保留原先的位置关系。

通过一个例子简单说明卷积神经网络的结构。假设我们需要识别一幅彩色图像,这幅图像具有四个通道ARGB(透明度和红绿蓝,对应了四幅相同大小的图像),假设卷积核大小为100*100,共使用100个卷积核w1到w100(从直觉来看,每个卷积核应该学习到不同的结构特征)。
用w1在ARGB图像上进行卷积操作,可以得到隐含层的第一幅图像;这幅隐含层图像左上角第一个像素是四幅输入图像左上角100*/100区域内像素的加权求和,以此类推。
同理,算上其他卷积核,隐含层对应100幅“图像”。每幅图像对是对原始图像中不同特征的响应。按照这样的结构继续传递下去。CNN中还有max-pooling等操作进一步提高鲁棒性。
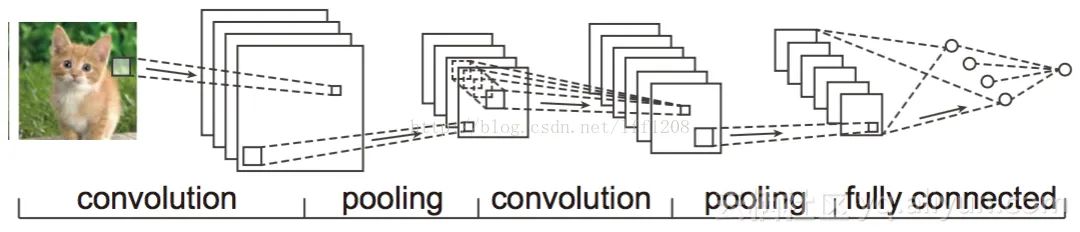
注意到最后一层实际上是一个全连接层,在这个例子里,我们注意到输入层到隐藏层的参数瞬间降低到了100100100=10^6个!这使得我们能够用已有的训练数据得到良好的模型。题主所说的适用于图像识别,正是由于CNN模型限制参数了个数并挖掘了局部结构的这个特点。顺着同样的思路,利用语音语谱结构中的局部信息,CNN照样能应用在语音识别中。
RNN形成
DNN无法对时间序列上的变化进行建模。然而,样本出现的时间顺序对于自然语言处理、语音识别、手写体识别等应用非常重要。为了适应这种需求,就出现了大家所说的另一种神经网络结构——循环神经网络RNN。
在普通的全连接网络或CNN中,每层神经元的信号只能向上一层传播,样本的处理在各个时刻独立,因此又被成为前向神经网络(Feed-forward Neural Networks)。而在RNN中,神经元的输出可以在下一个时间段直接作用到自身,即第i层神经元在m时刻的输入,除了(i-1)层神经元在该时刻的输出外,还包括其自身在(m-1)时刻的输出!表示成图就是这样的:
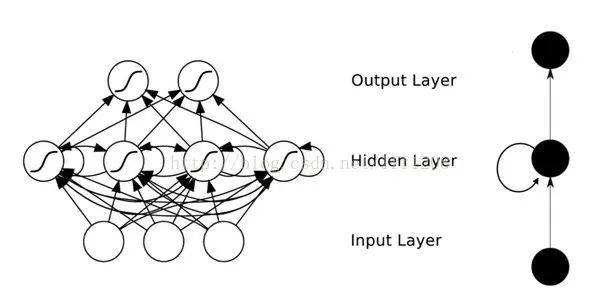
为方便分析,按照时间段展开如下图所示:
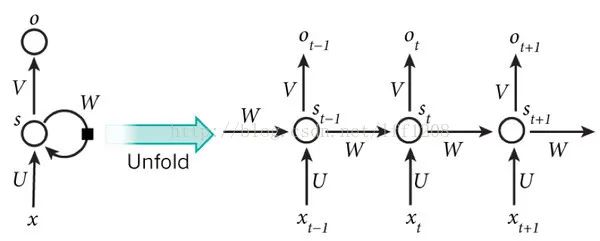
(t+1)时刻网络的最终结果O(t+1)是该时刻输入和所有历史共同作用的结果!这就达到了对时间序列建模的目的。RNN可以看成一个在时间上传递的神经网络,它的深度是时间的长度!正如我们上面所说,“梯度消失”现象又要出现了,只不过这次发生在时间轴上。
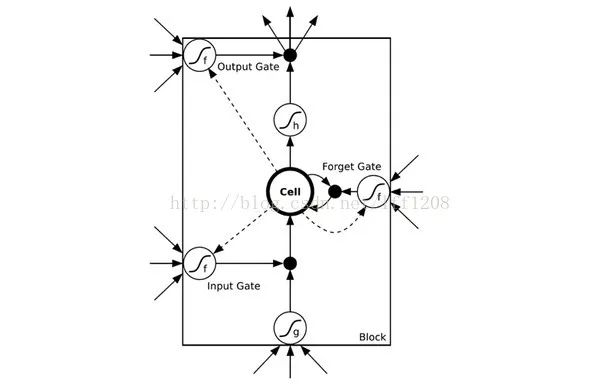
所以RNN存在无法解决长时依赖的问题。为解决上述问题,提出了LSTM(长短时记忆单元),通过cell门开关实现时间上的记忆功能,并防止梯度消失,LSTM单元结构如下图所示:
除了DNN、CNN、RNN、ResNet(深度残差)、LSTM之外,还有很多其他结构的神经网络。如因为在序列信号分析中,如果我能预知未来,对识别一定也是有所帮助的。因此就有了双向RNN、双向LSTM,同时利用历史和未来的信息。
事实上,不论是哪种网络,他们在实际应用中常常都混合着使用,比如CNN和RNN在上层输出之前往往会接上全连接层,很难说某个网络到底属于哪个类别。不难想象随着深度学习热度的延续,更灵活的组合方式、更多的网络结构将被发展出来。
简单总结如下:
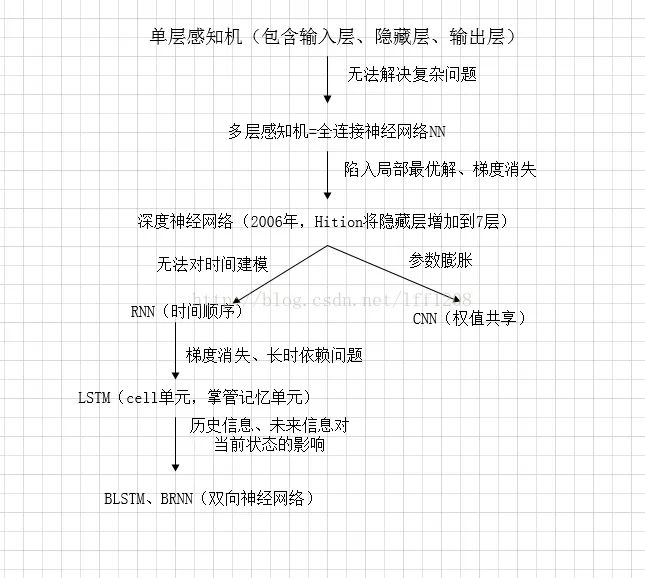
—版权声明—
仅用于学术分享,版权属于原作者。
若有侵权,请联系微信号:yiyang-sy 删除或修改!
