人工智能数学基础--不定积分1：概念与性质

一、引言

导数运算是根据一个函数求该函数对应导数的运算，导数本质上反映了函数在函数某点的运动态势，而不定积分则是根据一个已知的导函数求原函数，因此二者可以说是逆运算。

二、定义

2.1、 原函数定义

如果在区间I上，可导函数F(x)的导函数为f(x)，即对任一x∈I，都有：

F’(x)=f(x) 或 dF(x)=f(x)dx，

那么函数F(x)就称为f(x)(或f(x)dx)在区间I上的一个原函数。

2.2、原函数存在定理

定理：如果函数f(x)在区间I上连续，那么在区间I上存在可导函数F(x)，使对任一x∈I都有：

F’(x)=f(x)。

简单地说就是：连续函数一定有原函数。

2.3、不定积分定义

如果f(x)在区间I上有原函数，即有一个函数F(x)，使对任一x∈I，都有F’(x)=f(x)，那么，对任何常数C，显然也有：

[F(x)+C]’=f(x)

即对任何常数C，函数F(x)+C也是f(x)的原函数。这说明，如果f(x)有一个原函数，那么f(x)就有无限多个原函数。

定义：

在区间I上，函数f(x)的带有任意常数项的原函数称为f(x)(或f(x)dx)在区间I上的不定积分，记作:

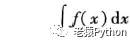
其中记号 ∫ 称为积分号，f(x)称为被积函数，f(x)dx称为被积表达式，x称为积

分变量。

由此定义及前面的说明可知，如果F(x)是f(x)在区间I上的一个原函数，那么F(x)+C就是f(x)的不定积分，即：∫ f(x)dx=F(x)+C

因而不定积分∫ f(x)dx可以表示f(x)的任意一个原函数。

函数f(x)对应的原函数几何图形称为f(x)的积分曲线。

由不定积分的定义可知：不定积分∫ f(x)dx是f(x)的原函数，所以：

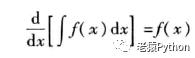
或：

d[∫f(x)dx] = f(x)dx

d[∫F’(x)dx]=∫dF(x)=F(x)+C

由此可见，微分运算（以记号d表示）与求不定积分的运算是互逆的，当记号d与∫连在一起时，要么相互抵消，要么抵消后差一个常数。

三、基本积分表

从导数运算可以推导出积分运算，以下十三个基本积分公式是不定积分的基础，必须熟记：

另外针对双曲函数（请参考《人工智能数学基础11：集合、函数及相关概念补充》）有如下积分公式：

下面是在基本积分公式基础上扩展出来的几个常用公式：

四、不定积分的性质

性质1：如果两个函数的不定积分都存在，则两个函数和的不定积分等于各自不定积分的和，即：

性质2：函数与常数的乘积的不定积分等于常数与函数不定积分的乘积，即：

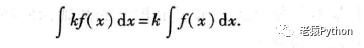
五、小结

本文介绍了不定积分的概念、性质以及基本的不定积分表，需要注意不定积分的运算公式只有加法和数乘的，没有象导数和微分那样还有乘除等运算公式。

说明：

本文内容是老猿学习同济版高数的总结，有需要原教材电子版以及OpenCV、Python基础知识、、图像处理原理介绍相关电子资料，或对文章内有有疑问咨询的，请扫博客首页左边二维码加微信公号，根据加微信公号后的自动回复操作。

更多人工智能数学基础请参考专栏《人工智能数学基础》。