轻量级图卷积网络LightGCN介绍和构建推荐系统示例

来源：DeepHub IMBA
本文约4500字，建议阅读9分钟
今天介绍的这个模型被称作：Light Graph Convolution Network 或 LightGCN¹。

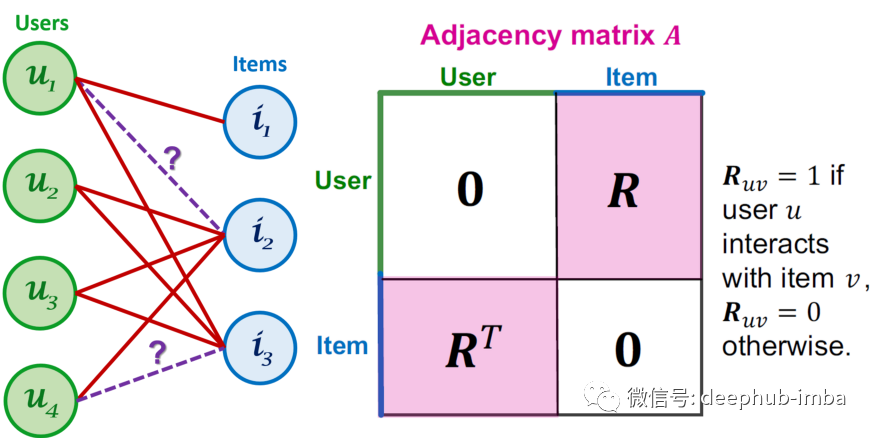
示例数据集

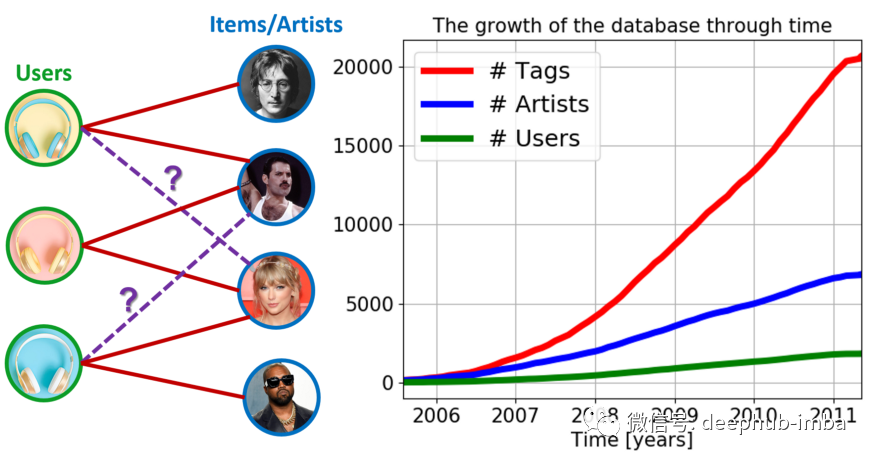
基于嵌入的模型

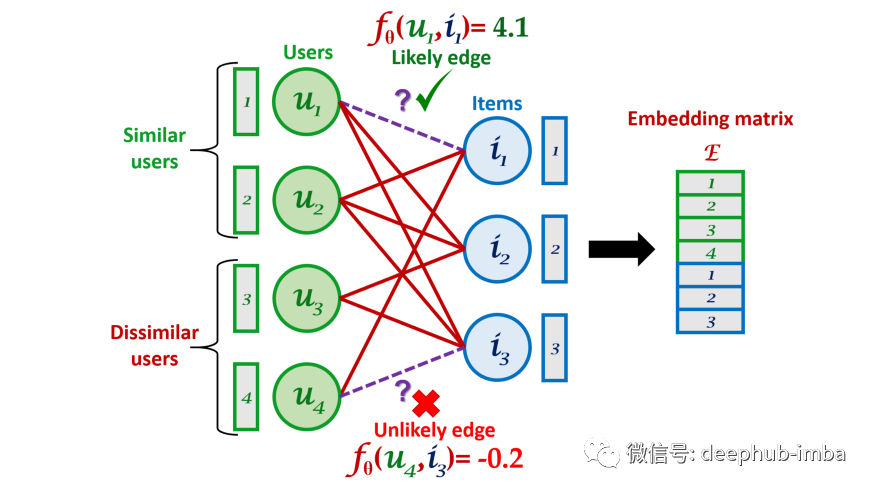
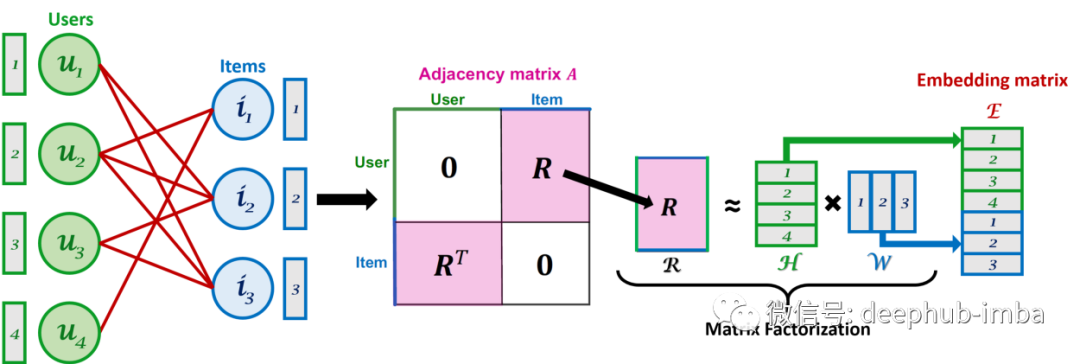
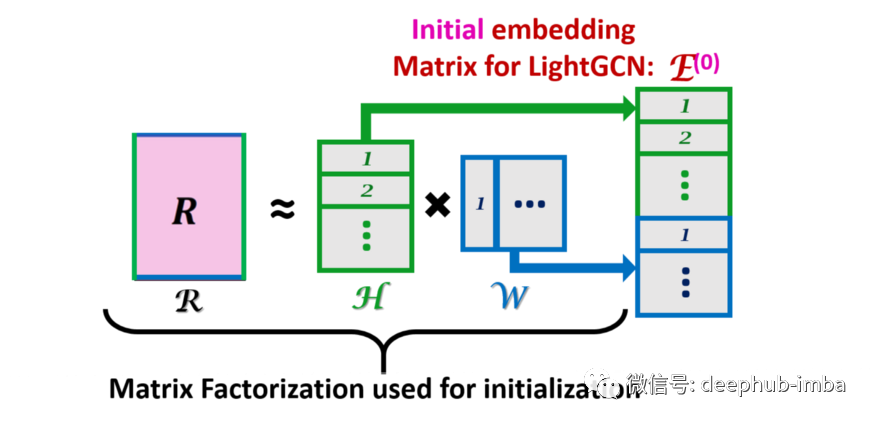
上图是矩阵分解(MF)过程与原始图以及嵌入矩阵²的关系。

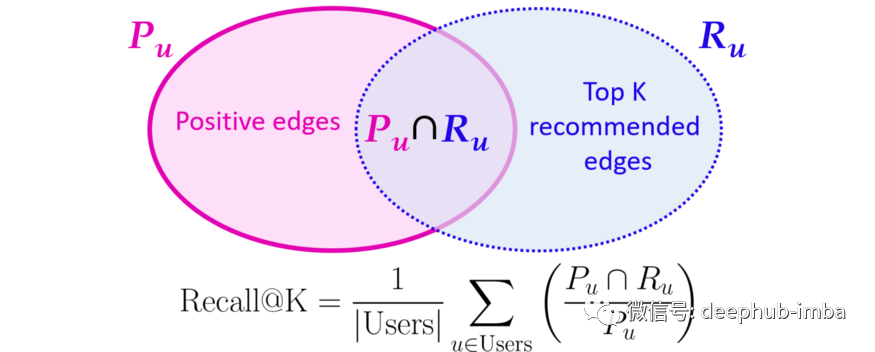
但是如何衡量性能呢？

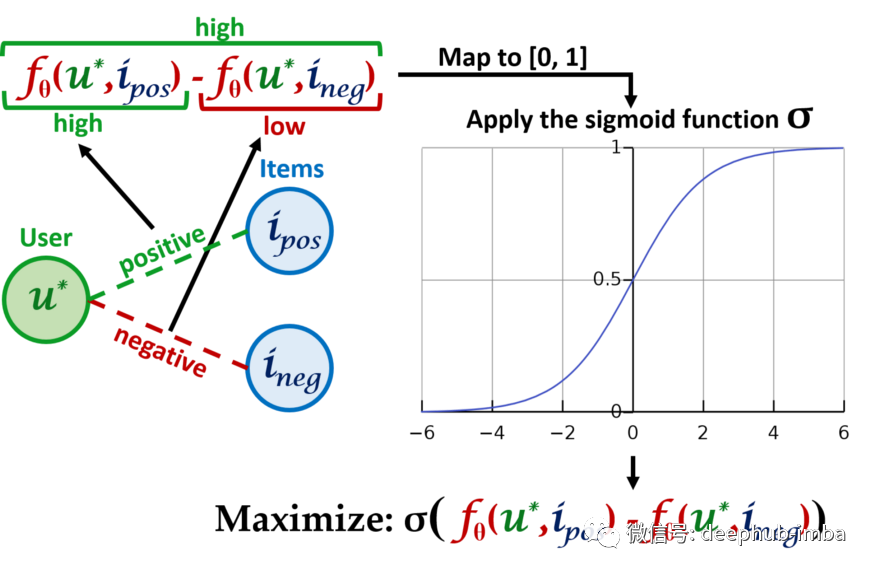
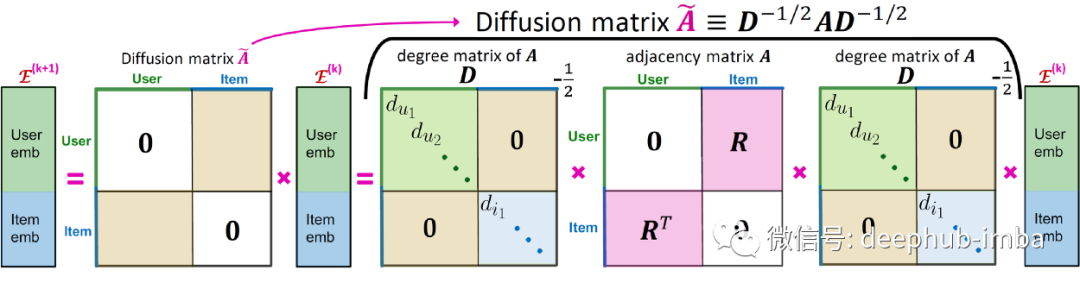
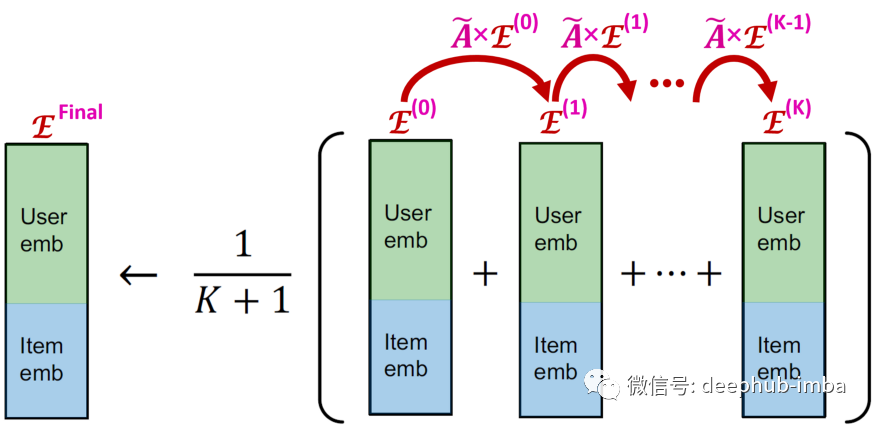
LightGCN

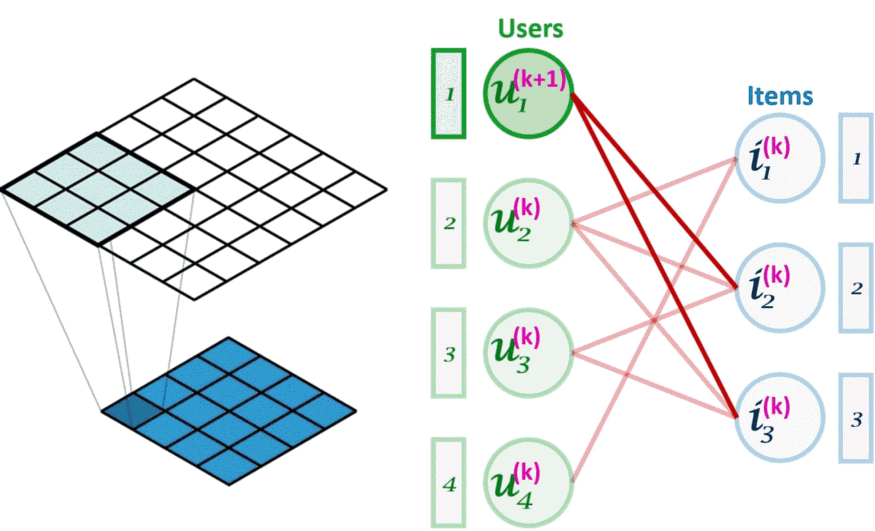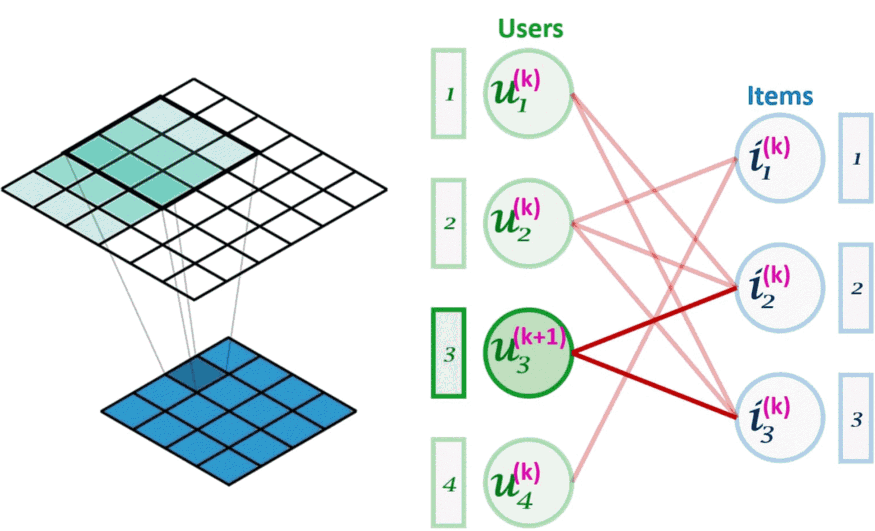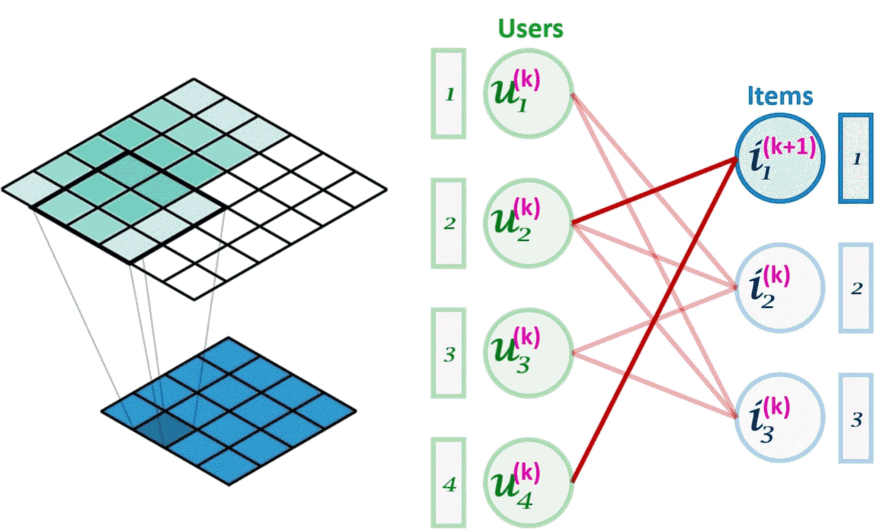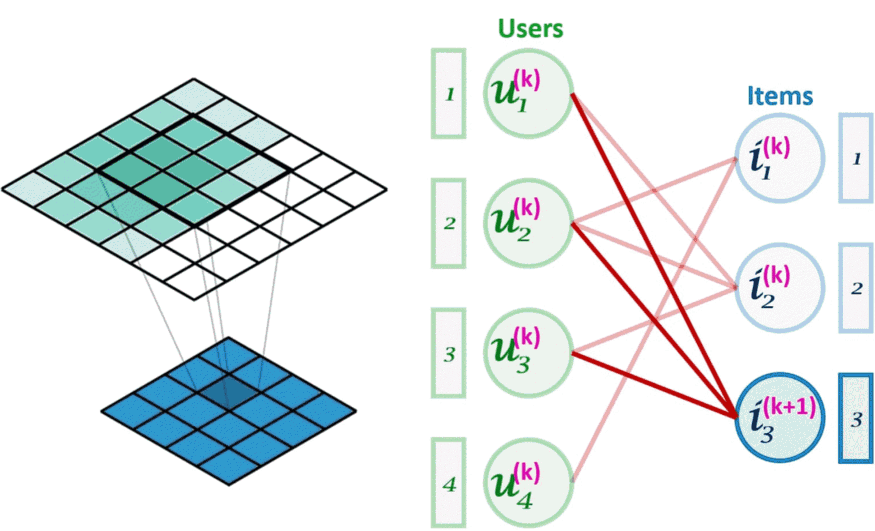
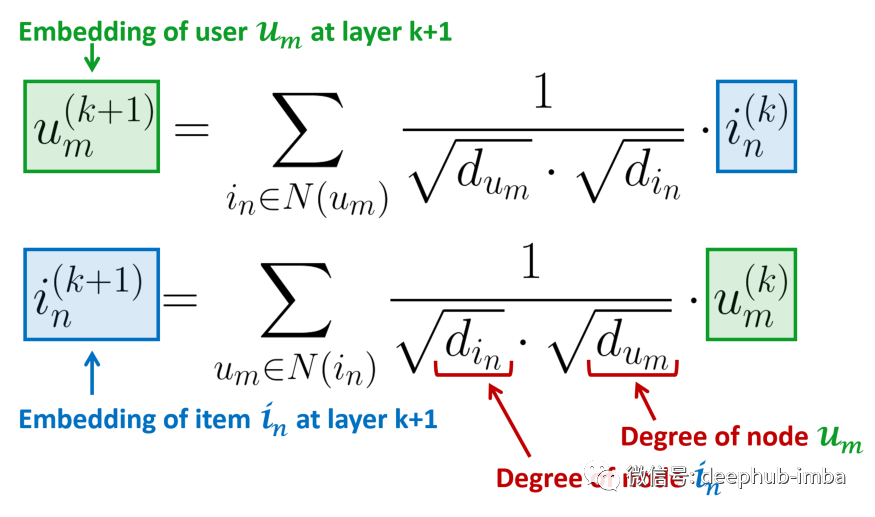
图像卷积（左）可以看作是图卷积（右）的一个特例。图卷积是一种节点置换不变的操作。

import torch
import torch.nn as nnimport torch.nn.functional as Fimport torch_scatterfrom torch_geometric.nn.conv import MessagePassing

class LightGCNStack(torch.nn.Module):  def __init__(self, latent_dim, args):      super(LightGCNStack, self).__init__()      conv_model = LightGCN      self.convs = nn.ModuleList()      self.convs.append(conv_model(latent_dim))      assert (args.num_layers >= 1), 'Number of layers is not >=1'      for l in range(args.num_layers-1):          self.convs.append(conv_model(latent_dim))
      self.latent_dim = latent_dim      self.num_layers = args.num_layers      self.dataset = None      self.embeddings_users = None      self.embeddings_artists = None
  def reset_parameters(self):      self.embeddings.reset_parameters()
  def init_data(self, dataset):      self.dataset = dataset      self.embeddings_users = torch.nn.Embedding(num_embeddings=dataset.num_users, embedding_dim=self.latent_dim).to('cuda')      self.embeddings_artists = torch.nn.Embedding(num_embeddings=dataset.num_artists, embedding_dim=self.latent_dim).to('cuda')
  def forward(self):      x_users, x_artists, batch = self.embeddings_users.weight, self.embeddings_artists.weight, \                                              self.dataset.batch
      final_embeddings_users = torch.zeros(size=x_users.size(), device='cuda')      final_embeddings_artists = torch.zeros(size=x_artists.size(), device='cuda')      final_embeddings_users = final_embeddings_users + x_users/(self.num_layers + 1)      final_embeddings_artists = final_embeddings_artists + x_artists/(self.num_layers+1)      for i in range(self.num_layers):          x_users = self.convs[i]((x_artists, x_users), self.dataset.edge_index_a2u, size=(self.dataset.num_artists, self.dataset.num_users))          x_artists = self.convs[i]((x_users, x_artists), self.dataset.edge_index_u2a, size=(self.dataset.num_users, self.dataset.num_artists))          final_embeddings_users = final_embeddings_users + x_users/(self.num_layers+1)          final_embeddings_artists = final_embeddings_artists + x_artists/(self.num_layers + 1)
      return final_embeddings_users, final_embeddings_artists
  def decode(self, z1, z2, pos_edge_index, neg_edge_index): # only pos and neg edges      edge_index = torch.cat([pos_edge_index, neg_edge_index], dim=-1) # concatenate pos and neg edges      logits = (z1[edge_index[0]] * z2[edge_index[1]]).sum(dim=-1) # dot product      return logits
  def decode_all(self, z_users, z_artists):      prob_adj = z_users @ z_artists.t() # get adj NxN      #return (prob_adj > 0).nonzero(as_tuple=False).t() # get predicted edge_list      return prob_adj
  def BPRLoss(self, prob_adj, real_adj, edge_index):      loss = 0      pos_scores = prob_adj[edge_index.cpu().numpy()]      for pos_score, node_index in zip(pos_scores, edge_index[0]):          neg_scores = prob_adj[node_index, real_adj[node_index] == 0]          loss = loss - torch.sum(torch.log(torch.sigmoid(pos_score.repeat(neg_scores.size()[0]) - neg_scores))) / \                  neg_scores.size()[0]
      return loss / edge_index.size()[1]
  def topN(self, user_id, n):      z_users, z_artists = self.forward()      scores = torch.squeeze(z_users[user_id] @ z_artists.t())      return torch.topk(scores, k=n)
class LightGCN(MessagePassing):  def __init__(self, latent_dim, **kwargs):      super(LightGCN, self).__init__(node_dim=0, **kwargs)      self.latent_dim = latent_dim
  def forward(self, x, edge_index, size=None):      return self.propagate(edge_index=edge_index, x=(x[0], x[1]), size=size)
  def message(self, x_j):      return x_j
  def aggregate(self, inputs, index, dim_size=None):      return torch_scatter.scatter(src=inputs, index=index, dim=0, dim_size=dim_size, reduce='mean')

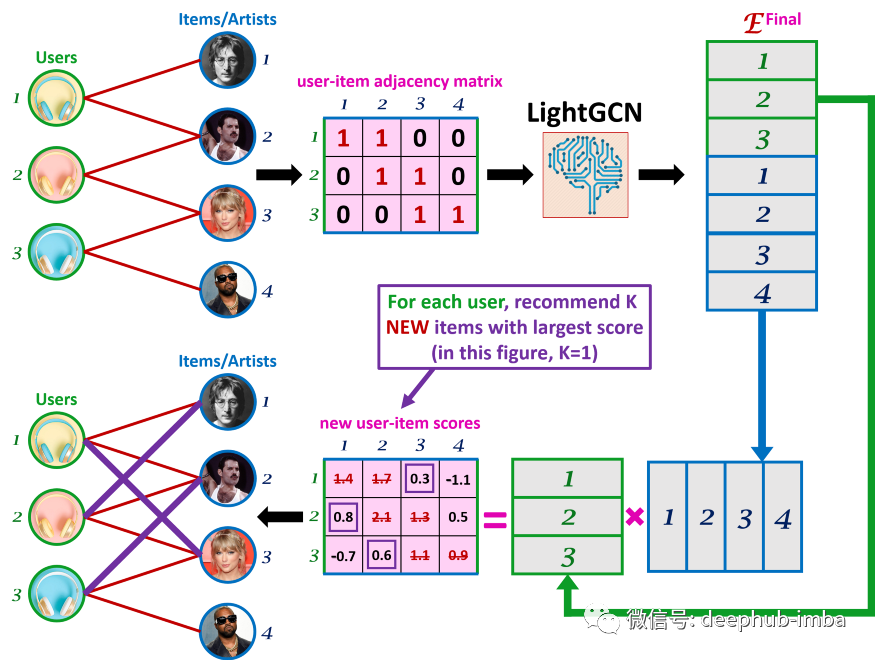
使用 LightGCN 进行预测

from functools import partial
import get_pyg_datafrom model import LightGCNStackimport torch
from src.data_preprocessing import TrainTestGeneratorfrom src.evaluator import Evaluatorfrom train_test import train, testfrom torch_geometric.utils import train_test_split_edgesimport time
import pandas as pd

class objectview(object):  def __init__(self, *args, **kwargs):      d = dict(*args, **kwargs)      self.__dict__ = d

# Wrapper for evaluationclass LightGCN_recommender:  def __init__(self, args):      self.args = objectview(args)      self.model = LightGCNStack(latent_dim=64, args=self.args).to('cuda')      self.a_rev_dict = None      self.u_rev_dict = None      self.a_dict = None      self.u_dict = None
  def fit(self, data: pd.DataFrame):      # Default rankings when userID is not in training set      self.default_recommendation = data["artistID"].value_counts().index.tolist()
      # LightGCN      data, self.u_rev_dict, self.a_rev_dict, self.u_dict, self.a_dict = get_pyg_data.load_data(data)      data = data.to("cuda")      self.model.init_data(data)      self.optimizer = torch.optim.Adam(params=self.model.parameters(), lr=0.001)
      best_val_perf = test_perf = 0
      for epoch in range(1, self.args.epochs+1):          start = time.time()          train_loss = train(self.model, data, self.optimizer)          val_perf, tmp_test_perf = test(self.model, (data, data))          if val_perf > best_val_perf:              best_val_perf = val_perf              test_perf = tmp_test_perf          log = 'Epoch: {:03d}, Loss: {:.4f}, Val: {:.4f}, Test: {:.4f}, Elapsed time: {:.2f}'          print(log.format(epoch, train_loss, best_val_perf, test_perf, time.time()-start))
  def recommend(self, user_id, n):      try:          recommendations = self.model.topN(self.u_dict[str(user_id)], n=n)      except KeyError:
          recommendations = self.default_recommendation      else:          recommendations = recommendations.indices.cpu().tolist()          recommendations = list(map(lambda x: self.a_rev_dict[x], recommendations))      return recommendations

def evaluate(args):  data_dir = "../data/"  data_generator = TrainTestGenerator(data_dir)
  evaluator = Evaluator(partial(LightGCN_recommender, args), data_generator)  evaluator.evaluate()
  evaluator.save_results('../results/lightgcn.csv', '../results/lightgcn_time.csv')  print('Recall:')  print(evaluator.get_recalls())  print('MRR:')  print(evaluator.get_mrr())

if __name__=='__main__':  # best_val_perf = test_perf = 0  # data = get_pyg_data.load_data()  #data = train_test_split_edges(data)
  args = {'model_type': 'LightGCN', 'num_layers': 3, 'batch_size': 32, 'hidden_dim': 32,        'dropout': 0, 'epochs': 1000, 'opt': 'adam', 'opt_scheduler': 'none', 'opt_restart': 0, 'weight_decay': 5e-3,        'lr': 0.1, 'lambda_reg': 1e-4}
  evaluate(args)

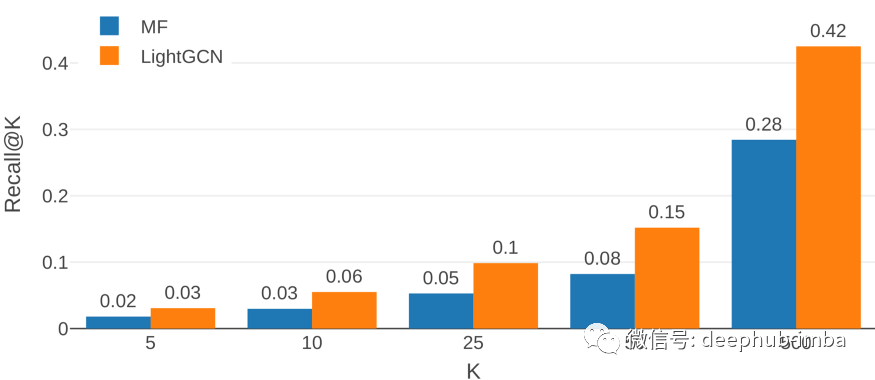
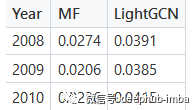
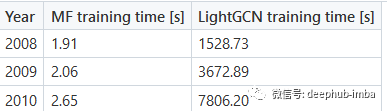
结果对比

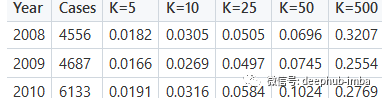
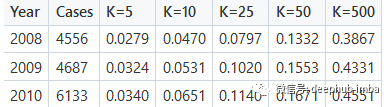
通过矩阵分解得到Recall@K分数

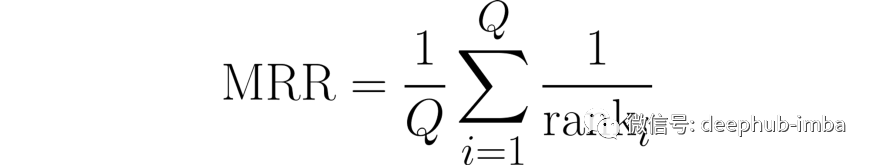
1. Xiangnan He, Kuan Deng, Xiang Wang, Yan Li, Yongdong Zhang, and Meng Wang.  Lightgcn: Simplifying and powering graph convolution network for  recommendation. In Proceedings of the 43rd International ACM SIGIR  conference on research and development in Information Retrieval, pages  639–648, 2020. arXiv:2002.02126  

2. Visualizations taken from lecture given by Jure Leskovec, available at

   http://web.stanford.edu/class/cs224w/slides/13-recsys.pdf

3. Iván Cantador, Peter Brusilovsky, and Tsvi Kuflik. 2nd workshop on  information heterogeneity and fusion in recommender systems (hetrec  2011). In Proceedings of the 5th ACM conference on Recommender systems,  RecSys 2011, New York, NY, USA, 2011. ACM.

4. 本文代码

   https://github.com/tm1897/mlg_cs224w_project/tree/main(Authors: Ermin Omeragić, Tomaž Martičič, Jurij Nastran)