人工智能数学基础---定积分1:定积分的概念以及近似计算

一、引言
在日常计算中,需要进行一些非线性的计算,如曲边型的面积和变速直线运动的总里程等,由于非线性,导致这些计算不能使用常规的方法来进行。但如果将这些计算涉及的函数在其定义区间上细分成n(n->∞)个区间,在每个细分的区间内,则可以用线性的方法近似用线性的方法来进行计算。
案例:曲边梯形面积和变速运动历程
函数f(x)在区间[a,b]上非负、连续,由直线x=a、x=b、y=0以及曲线y=f(x)构成的图形(如图5-1)称为曲边梯形:

其中曲线y=f(x)称为曲边。
将区间[a,b]分成n个区间,每个区间的长度记为Δxi,在每个区间上取任一点 ξi,则以每个小区间Δxi为底以f( ξi)为高的窄矩形近似替代每个小曲边梯形(或梯形),则整个曲边梯形的面积A可以用下列公式近似计算:
A ≈ f( ξ1) Δx1+f( ξ2) Δx2+…+f( ξn) Δxn
为了保证小区间的长度无限小,要求λ = max(Δxi)->0,此时n->∞,取上式的极限,便得到曲边梯形的面积计算公式:
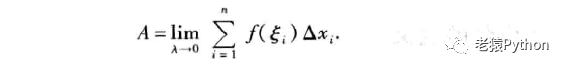
类似地,将时间区间[T1,T2]分成n个区间Δti,最大区间长为λ,在每个区间内任取一个变速运动速度v(Ti),则变速运动的总里程s计算公式可以表示如下:

二、定积分的定义
有上面曲边梯形的面积计算公式和变速运动的里程计算公式,都由一个自变量及其变化区间所决定,其结果是具有相同结构的一种特定和的极限,通过概括这些计算公式共同的本质和特性,就可以得到定积分的定义:
设函数f(x)在区间[a,b]上有界,在[a,b]中任意插入若干个分点:a=x0<x1<x2<…<xn-1<xn=b,把区间[a,b]分成若干个小区间:[x0,x1],[x1,x2],…,[xn-1,xn]
各个小区间的长度为:Δx1 = x1 - x0、Δx2 = x2 - x1、…、Δxn = xn - xn-1
在每个小区间[xi-1,xi]上任取一点ξi,作函数值f(ξi)与小区间长度Δxi的乘积f(ξi)Δxi(i=1,2,…,n),并作出和:
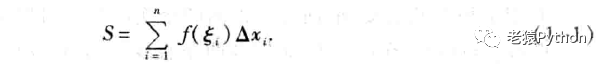
记λ=max{Δx1,Δx2,…,Δxn},如果当λ->0时,和S的极限总存在,且与闭区间[a,b]的分法及点ξi的取法无关,那么成极限I为函数f(x)在区间[a,b]上的定积分(简称积分),记作: ,即:
,即:
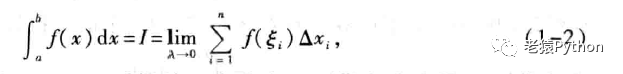
其中f(x)叫做被积函数,f(x)dx称为被积表达式,x称为积分变量,a称为积分下限,b称为积分上限,[a,b]称为积分区间。和式:
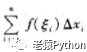
称为f(x)的积分和。如果f(x)在区间[a,b]上的定积分存在,那么就成f(x)在区间[a,b]上可积。
可以看到定积分和不定积分在被积函数、被积表达式、积分变量上的含义是一致的。
注意:定积分的值只与积分区间和被积函数相关,与积分变量无关。
三、函数f(x)在区间[a,b]上可积的充分条件
定理1:函数f(x)在区间[a,b]上连续,则f(x)在区间[a,b]上可积
定理2:函数f(x)在区间[a,b]上有界,且只有有限个间断点,则f(x)在区间[a,b]上可积
四、定积分的几何意义
在[a,b]上f(x)≥0时,函数f(x)在区间[a,b]上的定积分表示由曲线y=f(x)、两条直线x=a、x三b与x轴所围成的曲边梯形的面积;
在[a,b]上f(x)≤0时,由曲线y=f(x)、两条直线x=a、x=b与x轴所围成的曲边梯形位于x轴的下方,函数f(x)在区间[a,b]上的定积分表示上述曲边梯形面积的负值;
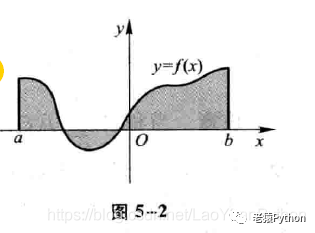
在[a,b]上f(x)既取得正值又取得负值时,函数(x)的图形某些部分在 x轴的上方,而其他部分在x轴下方(如图5-2),此时函数f(x)在区间[a,b]上的定积分表示x轴上方图形面积减去x轴下方图形面积所得之差。
五、利用积分定义计算定积分案例

六、定积分的近似计算
1、矩形法
由于函数f(x)在区间[a,b]上的定积分与闭区间[a,b]的分法及每个小区间内点ξi的取法无关,为了求连续函数f(x)在区间[a,b]上的定积分,可采取把区间[a,b]进行n等分的分法,即分成n个等长的区间,每个小区间的长度Δxi=(b-a)/n。
如果在小区间[xi-1,xi]上,取ξi = xi-1,则有:
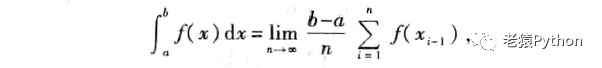
由于对于任意确定的正整数n,有:
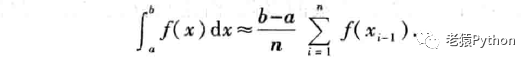
记f(xi)=yi(i=0,1,2,…,n),则上式可记作:
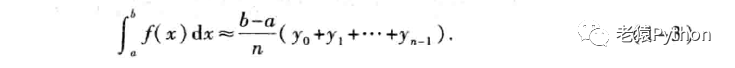
类似地,如果在小区间[xi-1,xi]上,取ξi = xi,则有:

这种求定积分近似值的方法称为矩形法,公式(1-3)、(1-4)称为矩形法公式。
矩形法的几何意义:用窄条矩形的面积作为窄条曲边梯形面积的近似值,整体上用台阶形的面积作为曲边梯形面积的近似值,如图5-3所示:
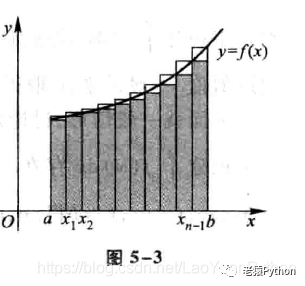
2、梯形法
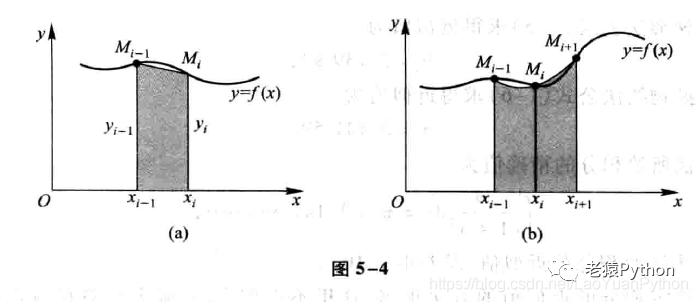
为了求连续函数f(x)在区间[a,b]上的定积分,同样采取把区间[a,b]进行n等分,设f(xi)=yi,曲线上的点(xi,yi)记作Mi,i=(0,1,2,…,n)。将曲线y=f(x)上的小弧段Mi-1Mi用直线段Mi-1Mi代替,也就是把窄条曲边梯形用窄条梯形代替,如图5-4(a)所示:
由此得到定积分的近似计算值为:
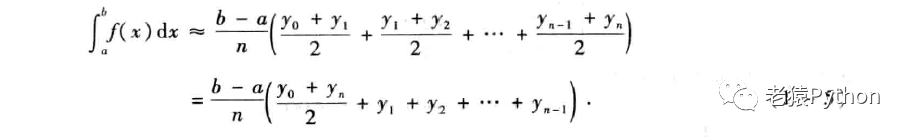
可以看出,梯形法所得的近似值是矩形法(1-3)、(1-4)所得两个近似值的平均。
3、抛物线法
抛物线法又称辛普森(Simpson)法,是将曲线y=f(x)上的两个弧段Mi-1Mi和MiMi+1合起来,用通过Mi-1、Mi和Mi+1三点的抛物线y=px2+qx+r代替,如图5-4(b)所示。经推导可以得,以此抛物线弧段为曲边,以[Mi-1,Mi+1]为底的曲边梯形面积为:
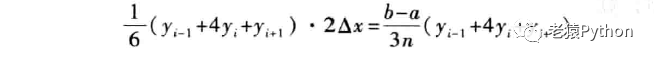
取n为偶数,得到定积分的的近似值为:
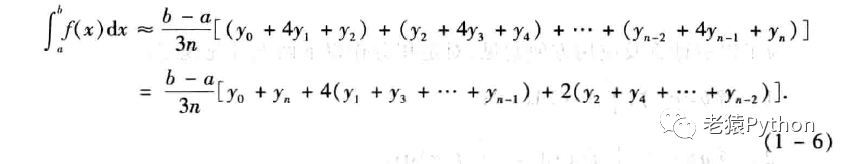
除了以上三个方法外,定积分的近似计算方法还有很多,这里不再展开介绍。
4、案例
使用上述方法计算定积分的近似值时,先要指定n的值,然后将区间n等分得到各个xi的值,然后计算各f(xi)的函数值,再根据具体计算方法来计算对应定积分。
我们来看案例:

七、小结
本文介绍了定积分的概念、几何意义、用定义来求定积分的案例以及使用矩形法、梯形法和抛物线法求定积分近似值的方法和案例,需要注意定积分的近似计算方法还有很多,现在一些数学软件也支持定积分的近似计算,大家可以根据具体运算需要确定将积分区间等分份数以及近似计算方法来具体运用。
说明:
本文内容是老猿学习同济版高数的总结,有需要原教材电子版以及OpenCV、Python基础知识、、图像处理原理介绍相关电子资料,或对文章内有有疑问咨询的,请扫博客首页左边二维码加微信公号,根据加微信公号后的自动回复操作。
更多人工智能数学基础请参考专栏《人工智能数学基础》。
