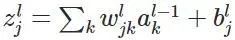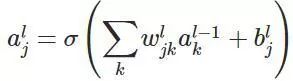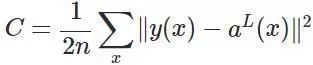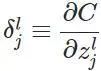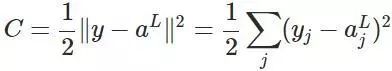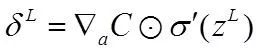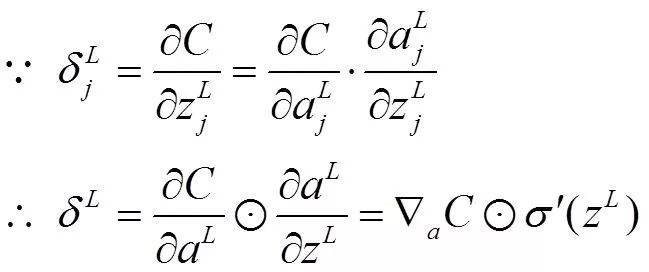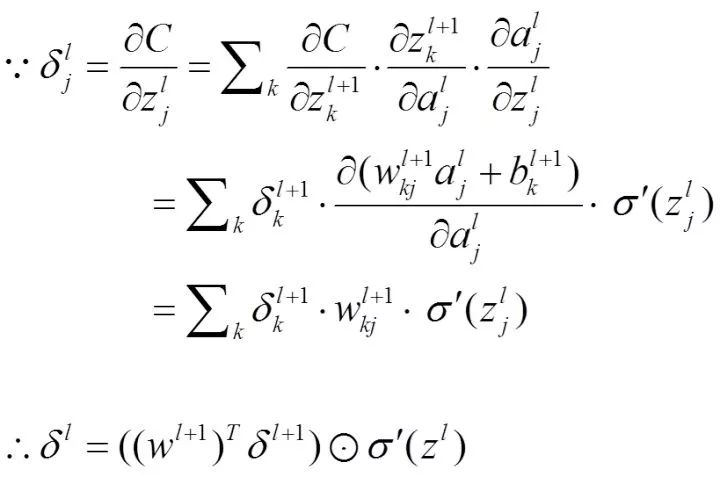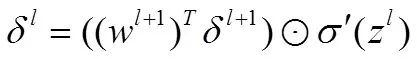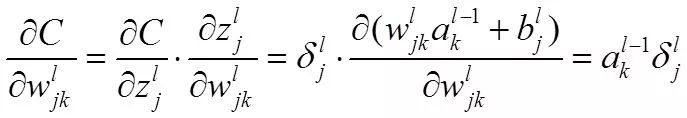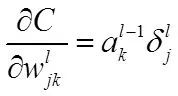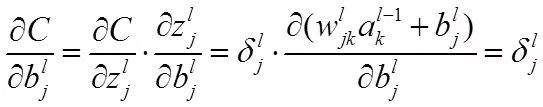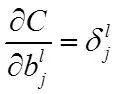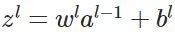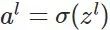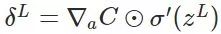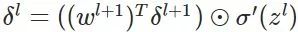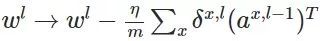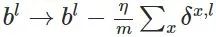点击上方“小白学视觉”，选择加"星标"或“置顶”

重磅干货，第一时间送达

一、人工神经网络简述

下面开始说神经网络。注意，当我们说N层神经网络的时候，我们没有把输入层算入（因为输入层只是输入数据）。因此，单层的神经网络就是没有隐层的（输入直接映射到输出）。而对于输出层，也和神经网络中其他层不同，输出层的神经元一般是不会有激活函数的（或者也可以认为它们有一个线性相等的激活函数）。这是因为最后的输出层大多用于表示分类评分值，因此是任意值的实数，然后用softmax得到分类值，或者直接某种实数值的目标数（比如在回归中）。对于各种激活函数之后会写。    

全连接层及其网络

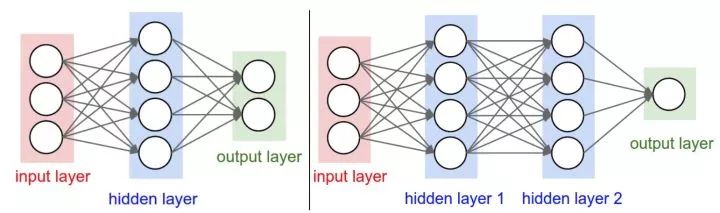
对于普通神经网络，最普通的层的类型是全连接层（fully-connected layer）。全连接层中的神经元与其前后两层的神经元是完全成对连接的，但是在同一个全连接层内的神经元之间没有连接。下面是两个神经网络的图例，都使用的全连接层：

左边是一个2层神经网络，隐层由4个神经元（也可称为单元（unit））组成，输出层由2个神经元组成。右边是一个3层神经网络，两个含4个神经元的隐层。

注意：层与层之间的神经元是全连接的，但是层内的神经元不连接。

其中，用来度量神经网络的尺寸的标准主要有两个：一个是神经元的个数，另一个是参数的个数，用上面图示的两个网络举例：

• 第一个网络有4+2=6个神经元（输入层不算），[3x4]+[4x2]=20个权重，还有4+2=6个偏置，共26个可学习的参数。

• 第二个网络有4+4+1=9个神经元，[3x4]+[4x4]+[4x1]=32个权重，4+4+1=9个偏置，共41个可学习的参数。

值得注意的是：现代神经网络能包含约1亿个参数，可由10-20层构成（这就是深度学习）。但那么多参数是很容易学不来的，所以在卷积神经网络中，会使用参数共享和局部链接的方式来减少参数，效果也更加的好。更多知识，后面讲卷积神经网络的时候会讲到。

二、反向传播链式法则简单理解

首先，反向传播的数学原理是“求导的链式法则” :

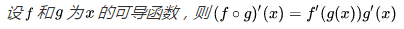
然后举个简单的例子说明链式求导：

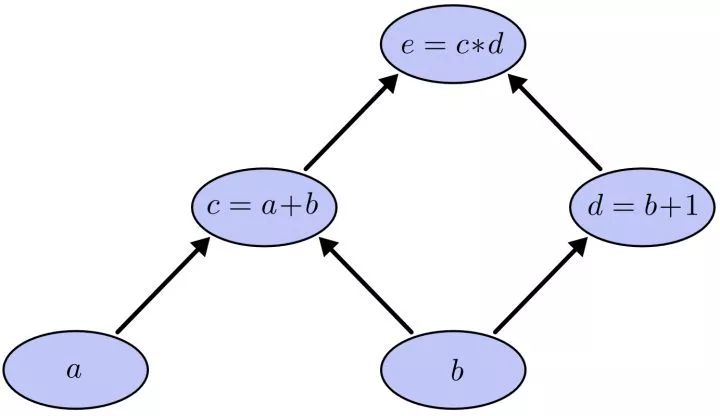
我们以求e=(a+b)*(b+1)的偏导为例。它的复合关系画出图可以表示如下：

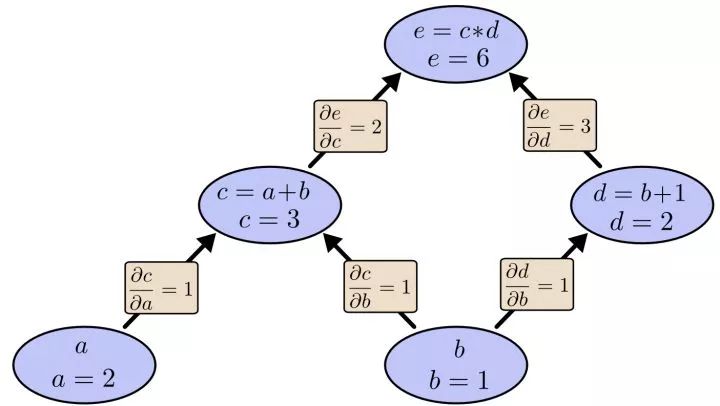
在图中，引入了中间变量c,d。为了求出a=2, b=1时，e的梯度，我们可以先利用偏导数的定义求出不同层之间相邻节点的偏导关系，如下图所示。

利用链式法则我们知道：

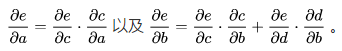
链式法则在上图中的意义是什么呢？其实不难发现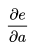，的值等于从a到e的路径上的偏导值的乘积，而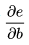的值等于从b到e的路径1(b-c-e)上的偏导值的乘积加上路径2(b-d-e)上的偏导值的乘积。也就是说，对于上层节点p和下层节点q，要求得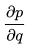，需要找到从q节点到p节点的所有路径，并且对每条路径，求得该路径上的所有偏导数之乘积，然后将所有路径的 “乘积” 累加起来才能得到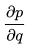的值。

但是，这就有一个比较大的问题，就是这样做是十分冗余的，很多路径被重复访问。比如上图中，a-c-e和b-c-e就都走了路径c-e。对于权值动则数万的深度模型中的神经网络，这样的冗余所导致的计算量是相当大的。

同样是利用链式法则，BP算法则机智地避开了这种冗余，它对于每一个路径只访问一次就能求顶点对所有下层节点的偏导值。（注意，这里他和普通链式求导计算方式不同的地方）

具体做法如下：正如反向传播(BP)算法的名字说的那样，BP算法是反向(自上往下)来寻找路径的。从最上层的节点e开始，初始值为1，以层为单位进行处理。对于e的下一层的所有子节点，将1乘以e到某个节点路径上的偏导值，并将结果“堆放”在该子节点中。等e所在的层按照这样传播完毕后，第二层的每一个节点都“堆放"些值，然后我们针对每个节点，把它里面所有“堆放”的值求和，就得到了顶点e对该节点的偏导。然后将这些第二层的节点各自作为起始顶点，初始值设为顶点e对它们的偏导值，以"层"为单位重复上述传播过程，即可求出顶点e对每一层节点的偏导数。

加深理解做法：以上图为例，节点c接受e发送的1*2并堆放起来，节点d接受e发送的1*3并堆放起来，至此第二层完毕，求出各节点总堆放量并继续向下一层发送。节点c向a发送2*1并对堆放起来，节点c向b发送2*1并堆放起来，节点d向b发送3*1并堆放起来，至此第三层完毕，节点a堆放起来的量为2，节点b堆放起来的量为2*1+3*1=5, 即顶点e对b的偏导数为5.

以上例子部分参考知乎胡逸夫回答：如何直观地解释 back propagation 算法？

三、神经网络中的反向传播

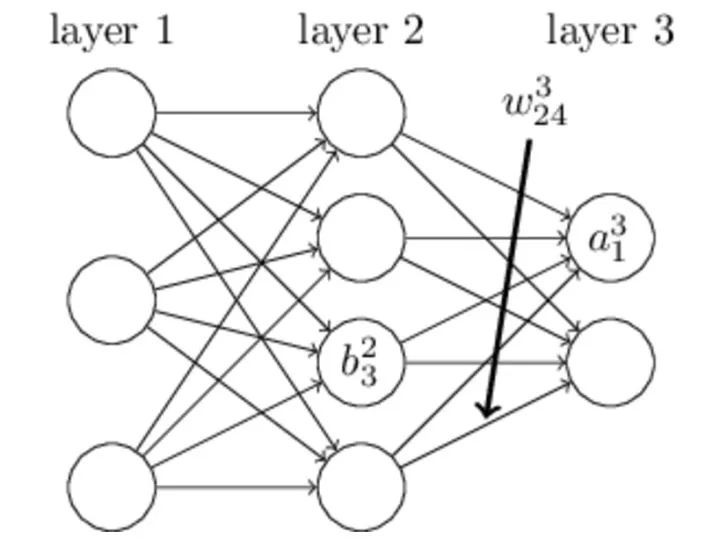
上面讲述的是在简化情况在的BP，下面讲述在神经网络中的反向传播，这里以简单的多层感知机为例：

如上图，我们先定义一个三层人工神经网络，layer1至layer3分别是输入层、隐藏层和输出层。首先定义说明一些变量：

然后，为了简单起见，我们定义代价函数为均方差损失函数（当然，现在很多不是用这个损失函数，至于为什么，会在下面一篇文章讲述）：

然后，更为了简单来算，我们以一个输入样本为例进行说明，此时代价函数表示为：

• 计算最后一层神经网络产生的错误：

其中，表示Hadamard乘积，用于矩阵或向量之间点对点的乘法运算（注意这里的维数应该相同），推导如下：

• 由后往前，计算每一层神经网络产生的错误，注意这里是反向回传错误的体现（这一步的推导最为关键）

所以我们得到：

这一步极为关键，需要前后换序、转置等操作，进行维度的适应，当然，知乎也有对这种做法的讲解：维数相容原则在反向传播的应用，可以一看！

• 然后，我们应用错误计算权重的梯度

所以得到：

• 最后，我们计算偏置的梯度

最终得到：

整理一下整体过程如下：

对于训练集中的每个样本x，设置输入层（Input layer）对应的激活值

• 前向传播：

• 反向传播：

下载1：OpenCV-Contrib扩展模块中文版教程

在「小白学视觉」公众号后台回复：扩展模块中文教程，即可下载全网第一份OpenCV扩展模块教程中文版，涵盖扩展模块安装、SFM算法、立体视觉、目标跟踪、生物视觉、超分辨率处理等二十多章内容。

下载2：Python视觉实战项目52讲

在「小白学视觉」公众号后台回复：Python视觉实战项目，即可下载包括图像分割、口罩检测、车道线检测、车辆计数、添加眼线、车牌识别、字符识别、情绪检测、文本内容提取、面部识别等31个视觉实战项目，助力快速学校计算机视觉。

下载3：OpenCV实战项目20讲

在「小白学视觉」公众号后台回复：OpenCV实战项目20讲，即可下载含有20个基于OpenCV实现20个实战项目，实现OpenCV学习进阶。

交流群

欢迎加入公众号读者群一起和同行交流，目前有SLAM、三维视觉、传感器、自动驾驶、计算摄影、检测、分割、识别、医学影像、GAN、算法竞赛等微信群（以后会逐渐细分），请扫描下面微信号加群，备注：”昵称+学校/公司+研究方向“，例如：”张三 + 上海交大 + 视觉SLAM“。请按照格式备注，否则不予通过。添加成功后会根据研究方向邀请进入相关微信群。请勿在群内发送广告，否则会请出群，谢谢理解~