图解快速排序-轻识

—

快速排序原理

快速排序用到了分治的思想，主要分为三步分治过程：

数组A[p..r]被划分为两个子数组A[p..q-1]和A[q+1..r]，使得A[p..q-1]中的每一个元素都小于A[q]，而A[q+1..r]的每一个元素大于等于A[q]，计算分割点q也是过程的一部分。

递归对A[p..q-1]进行划分直到无法划分为止，则A[p..q-1]处于有序状态，且每一个元素小于A[q]。同样的递归对A[q+1..r]进行划分直到无法划分为止，则A[q+1..r]处于有序状态，且每一个元素大于等于A[q]。

—

快速排序实现

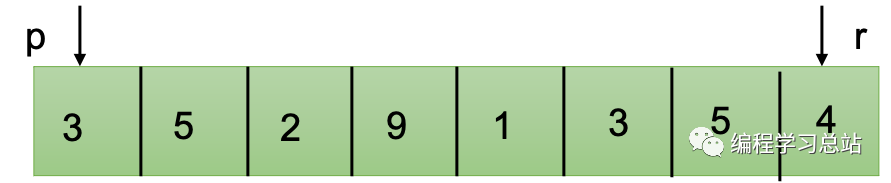
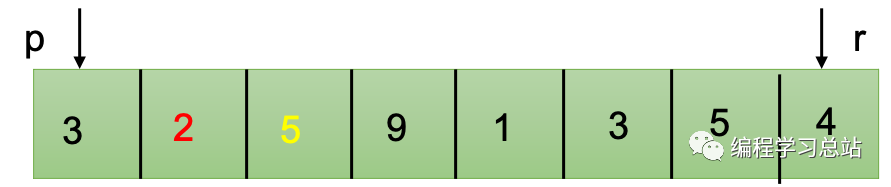
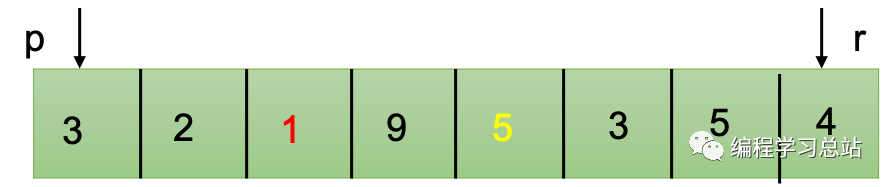
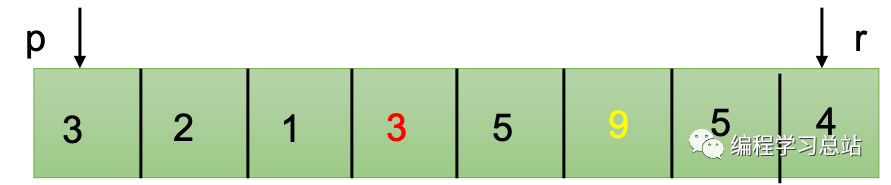
快速排序的核心是数组划分和分割点计算过程，我们用下图表示快速排序划分子序列的过程，现在有原始序列如下图，p、r分别对应0和7。

现在我们使用A[r]作为分割点x，从A[p]开始遍历序列，将小于x的值放在序列左边，大于等于x的值放在序列右边，并求出分割点q，下图则是分割过程。

经过一轮分割得到q位置作为分割点，A[p..q-1]序列小于A[q]而A[q+1..r]大于等于A[q]。后面不断分别对A[p..q-1]和A[q+1..r]进行递归划分则得到一个有序序列A[p..r]。

快速排序操作函数声明如下：

typedef int data_type_t;

extern void quick_sort(data_type_t *A, int p, int r);

划分序列获取分割点实现代码如下：

static void swap(data_type_t *x, data_type_t *y){
    if(x == NULL || y == NULL){
        return;
    }

    data_type_t temp = *x;
    *x = *y;
    *y = temp;
}

static int partision(data_type_t *A, int p, int r){
    data_type_t x = A[r]; //以最后一个元素作为主元
    int i = p - 1;
    int j = p;

    while(j < r){
        if(A[j] < x){
            i++;
            swap(&A[j], &A[i]); //比主元大的数放右边，小的数放在数组左边。
        }
        j++;
    }
    swap(&A[++i], &A[r]); //主元作为分割点
    return i; //返回当前分割点位置
}

快速排序实现代码如下：

void quick_sort(data_type_t *A, int p, int r){
    if(p >= r){
        return;
    }
    int q = partision(A, p, r);
    quick_sort(A, p, q - 1);
    quick_sort(A, q + 1, r);
}

—

算法验证

下面我们写一个小程序验证算法的正确性。

#include <stdio.h>
#include "quick_sort.h"

int main() {
    int arr[10] = {8, 3, 5, 9, 1, 2, 78, 32, 6, 8};

    quick_sort(arr, 0, 9);

    int i = 0;
    for(i = 0; i < 10; i++){
        printf("%d ", arr[i]);
    }
    printf("\n");

    return 0;
}

编译输出结果如下：

1 2 3 5 6 8 8 9 32 78

算法完全正确。