(图解)为什么机器学习算法难以优化?一文详解算法优化内部机制
共 4251字,需浏览 9分钟
·
2021-08-02 23:14
点击左上方蓝字关注我们

转载自 | Datawhale
本文约3500字,建议阅读9分钟
本文介绍了一些关于机器学习和线性组合的部分问题以及缓解该问题的方法。
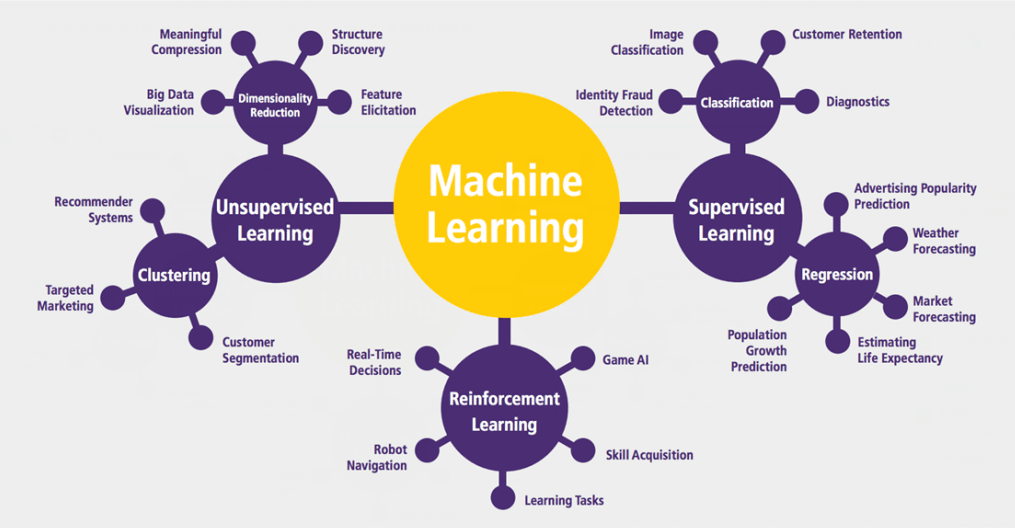
机器学习中的许多问题应该被视为多目标问题,但目前并非如此; 「1」中的问题导致这些机器学习算法的超参数难以调整; 检测这些问题何时发生几乎是不可能的,因此很难解决这些问题。
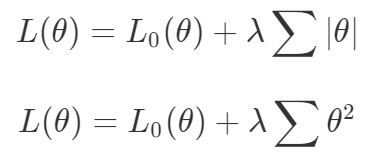
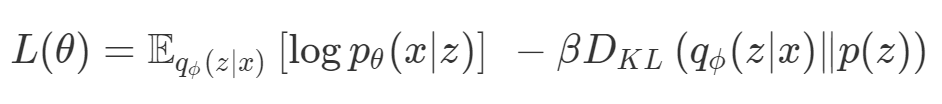
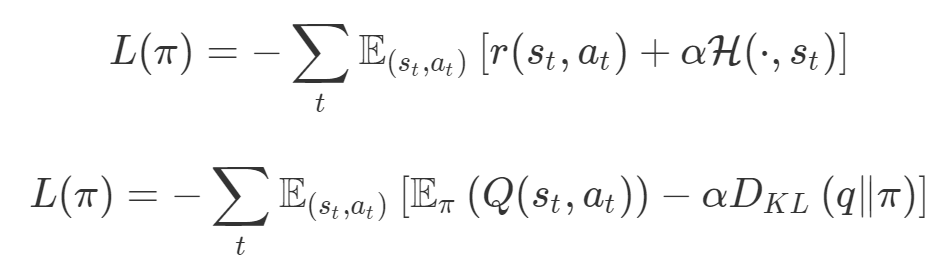
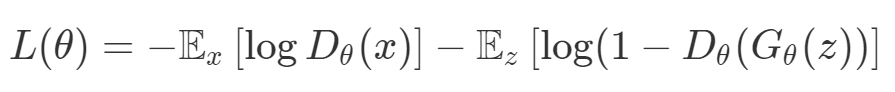
def loss(θ):return loss_1(θ) + loss_2(θ)loss_derivative = grad(loss)for gradient_step in range(200): gradient = loss_derivative(θ) θ = θ - 0.02 * gradientdef loss(θ, α):return loss_1(θ) + α*loss_2(θ)loss_derivative = grad(loss)for gradient_step in range(200): gradient = loss_derivative(θ, α=0.5) θ = θ - 0.02 * gradient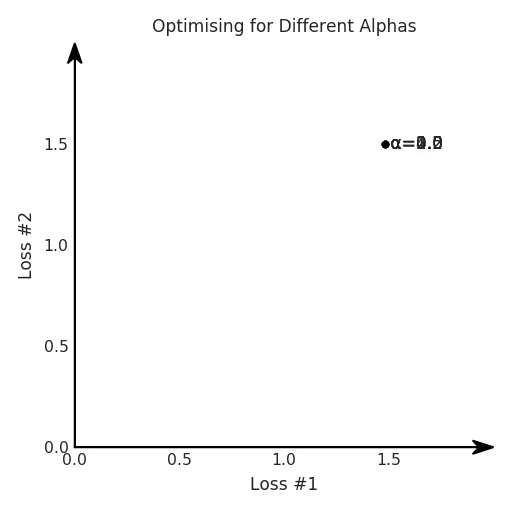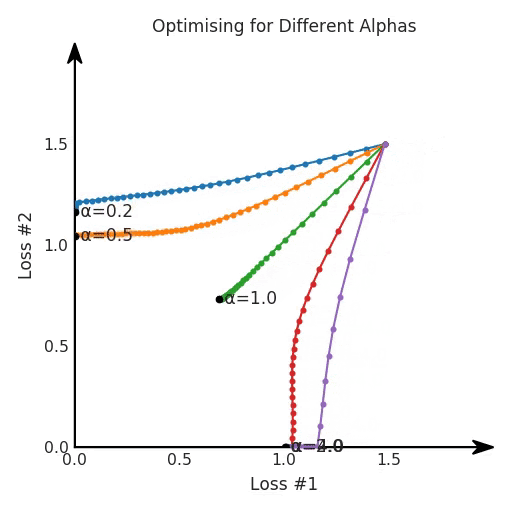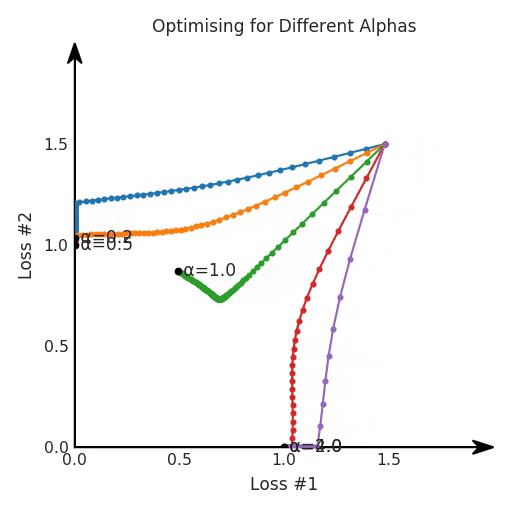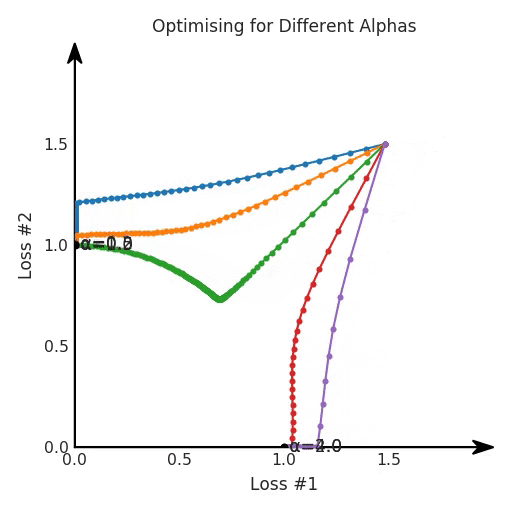
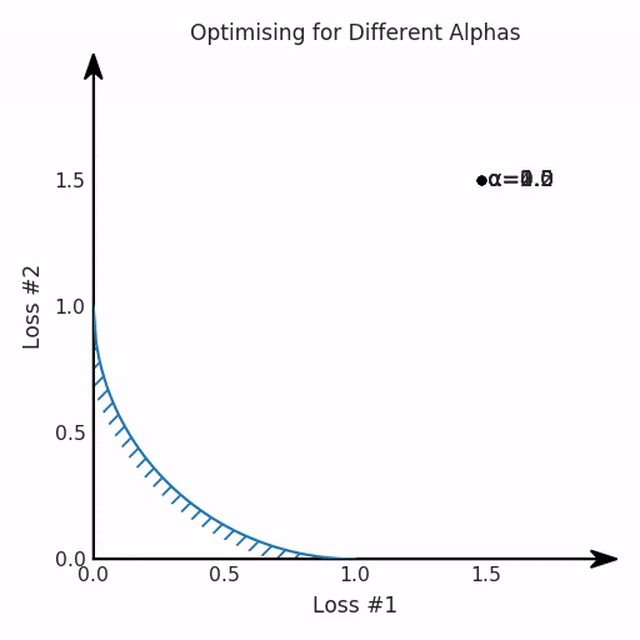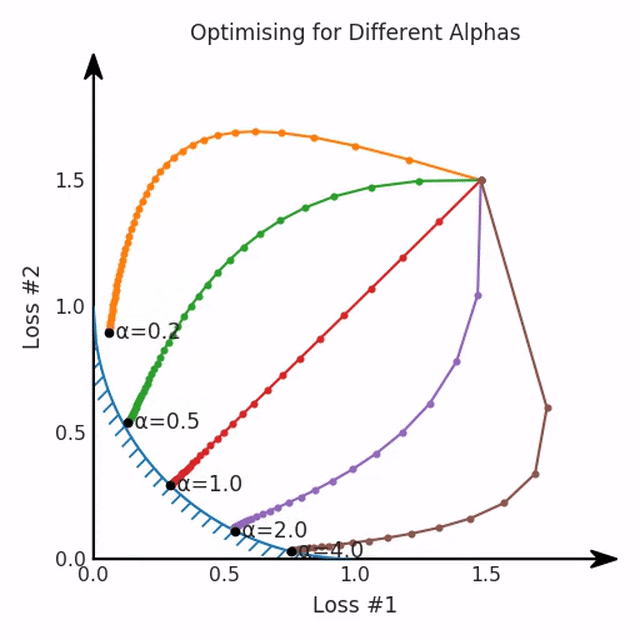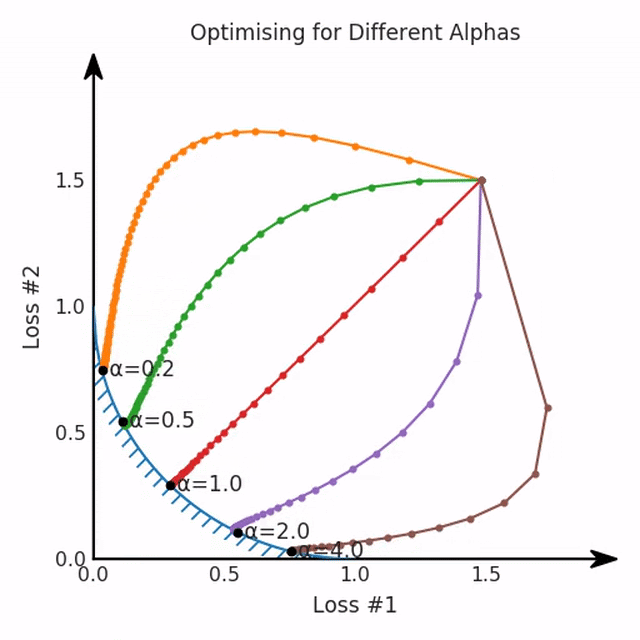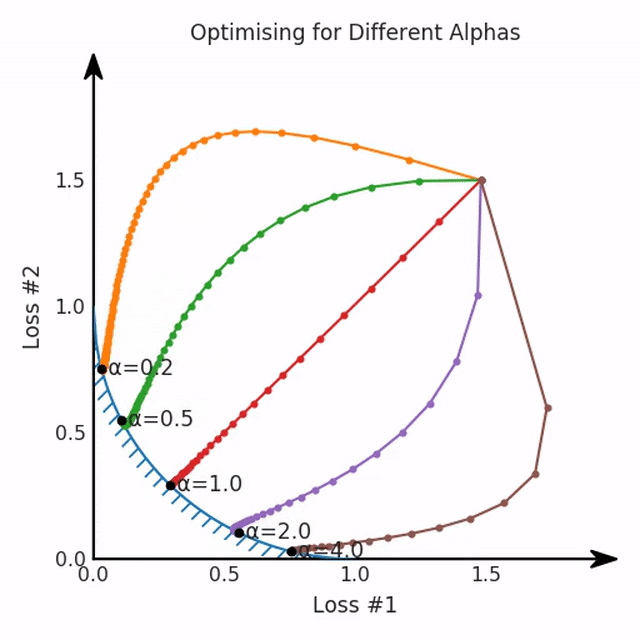
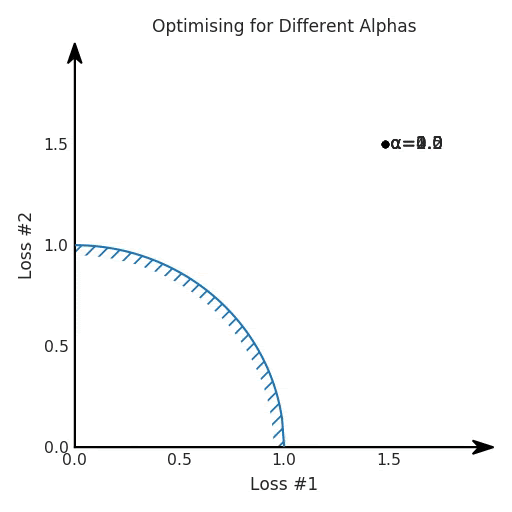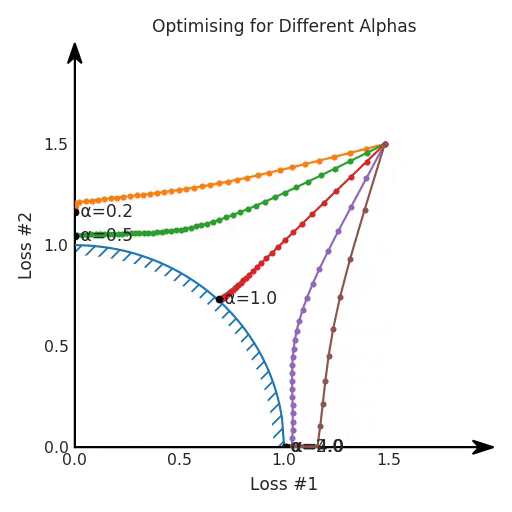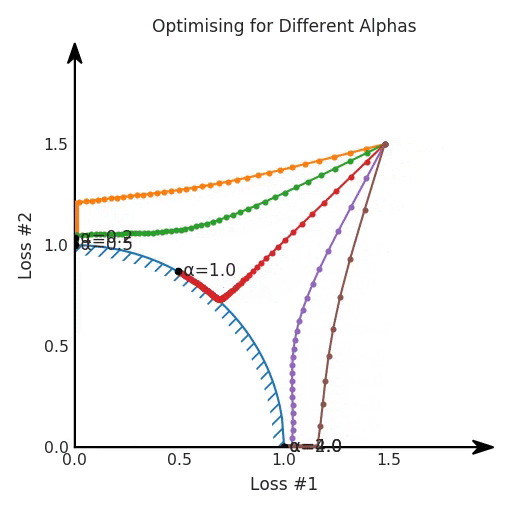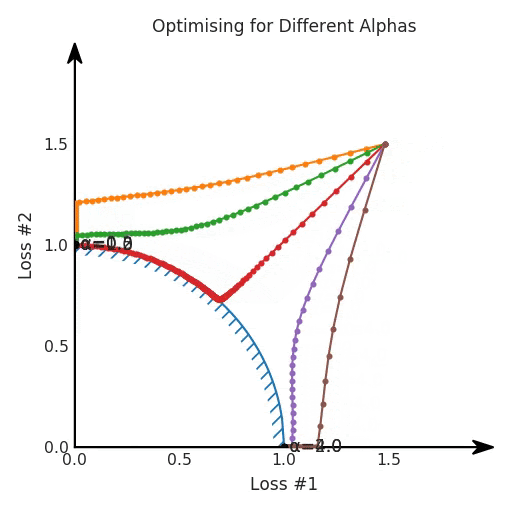
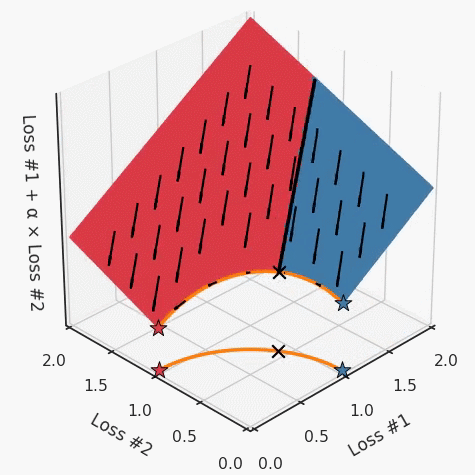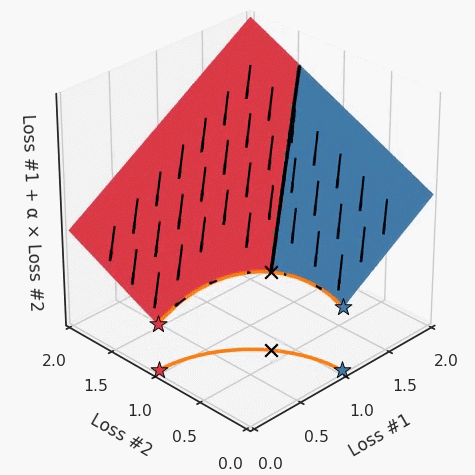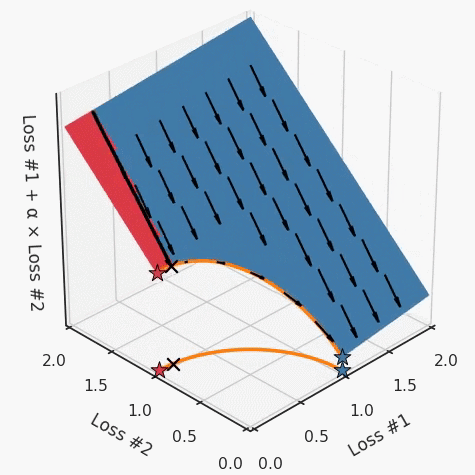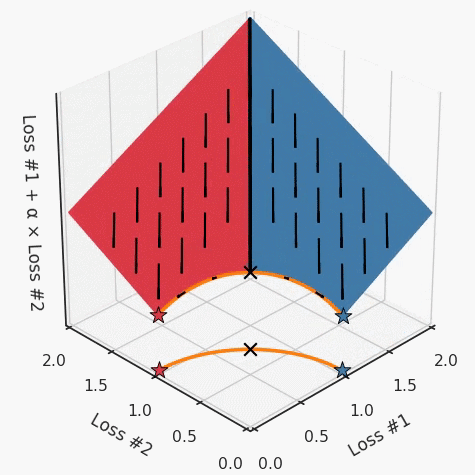
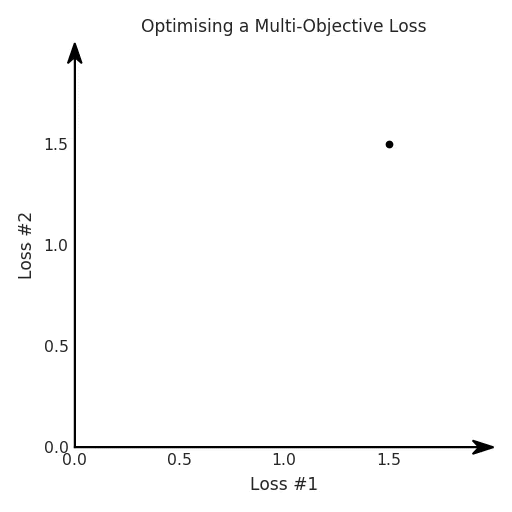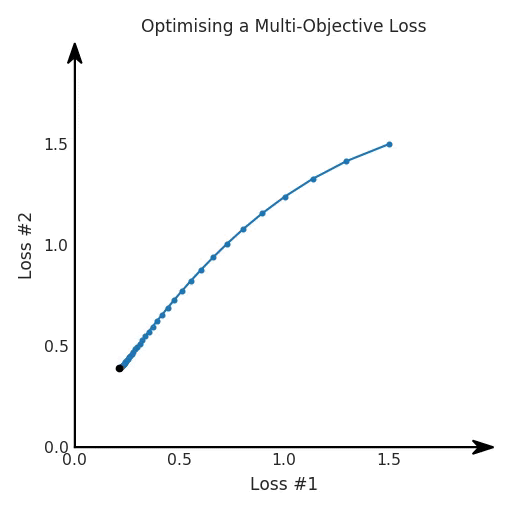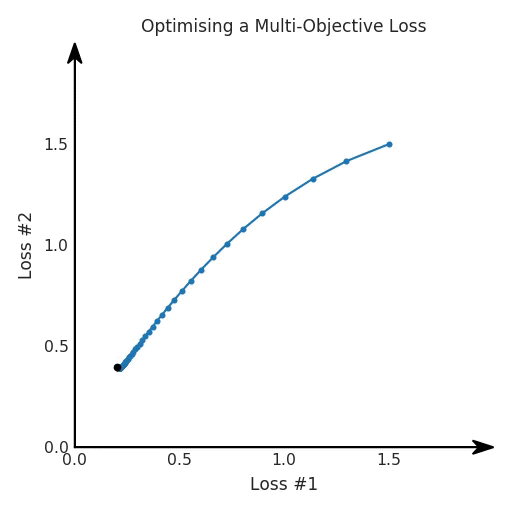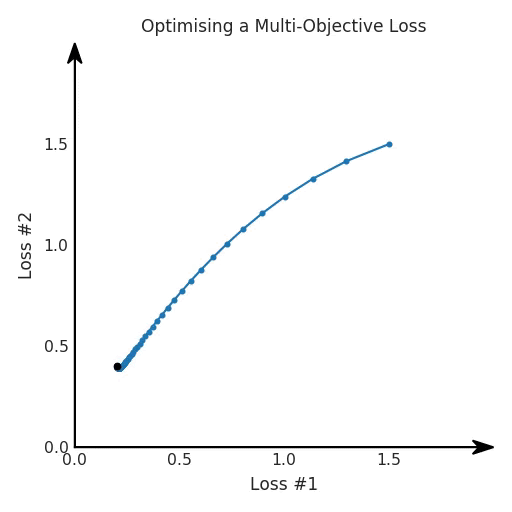
第一,即使没有引入超参数来权衡损失,说梯度下降试图在反作用力之间保持平衡也是不正确的。根据模型可实现的解,可以完全忽略其中一种损失,而将注意力放在另一种损失上,反之亦然,这取决于初始化模型的位置;
第二,即使引入了超参数,也将在尝试后的基础上调整此超参数。研究中往往是运行一个完整的优化过程,然后确定是否满意,再对超参数进行微调。重复此优化循环,直到对性能满意为止。这是一种费时费力的方法,通常涉及多次运行梯度下降的迭代;
第三,超参数不能针对所有的最优情况进行调整。无论进行多少调整和微调,你都不会找到可能感兴趣的中间方案。这不是因为它们不存在,它们一定存在,只是因为选择了一种糟糕的组合损失方法;
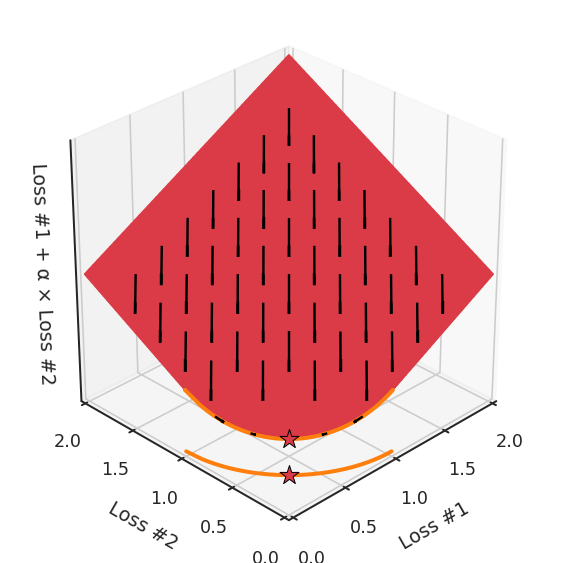
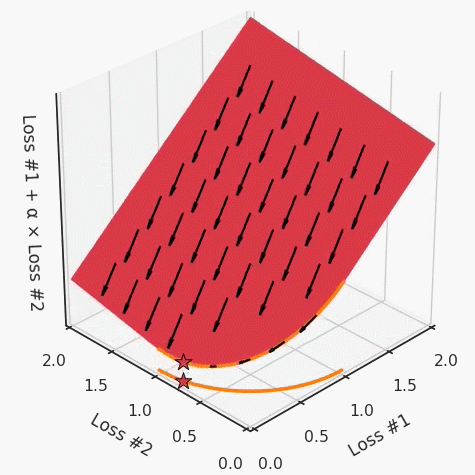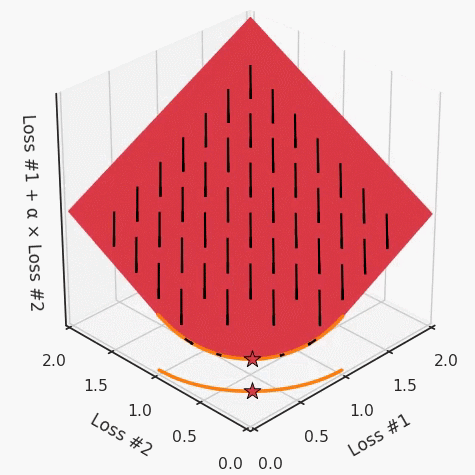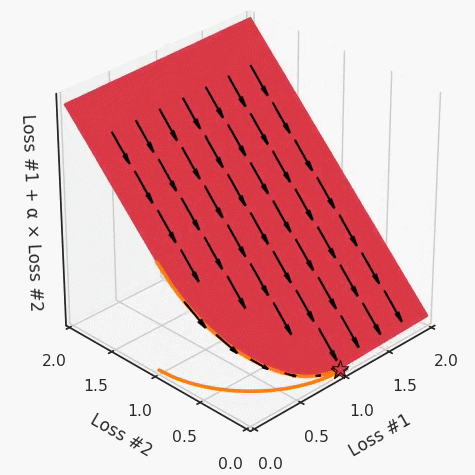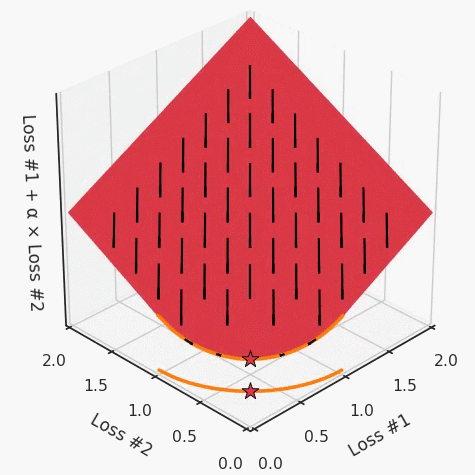
第四,必须强调的是,对于实际应用,帕累托前沿面是否为凸面以及因此这些损失权重是否可调始终是未知的。它们是否是好的超参数,取决于模型的参数化方式及其影响帕累托曲线的方式。但是,对于任何实际应用,都无法可视化或分析帕累托曲线。可视化比原始的优化问题要困难得多。因此出现问题并不会引起注意;
最后,如果你真的想使用这些线性权重来进行权衡,则需要明确证明整个帕累托曲线对于正在使用的特定模型是凸的。因此,使用相对于模型输出而言凸的损失不足以避免问题。如果参数化空间很大(如果优化涉及神经网络内部的权重,则情况总是如此),你可能会忘记尝试这种证明。需要强调的是,基于某些中间潜势(intermediate latent),显示这些损失的帕累托曲线的凸度不足以表明你具有可调参数。凸度实际上需要取决于参数空间以及可实现解决方案的帕累托前沿面。
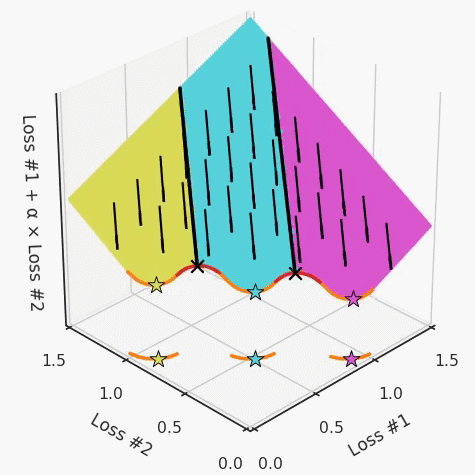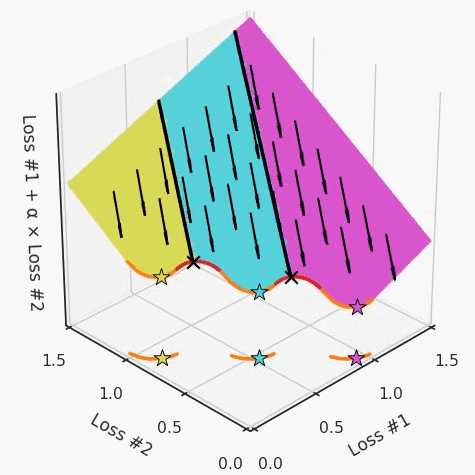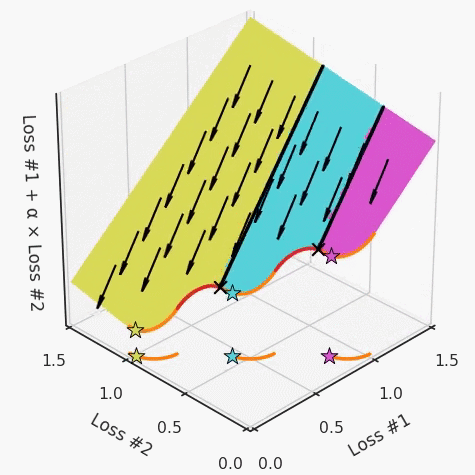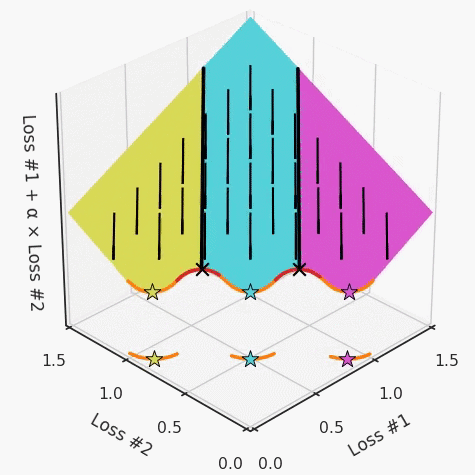
END
整理不易,点赞三连↓
