基于how-to-optimize-gemm初探矩阵乘法优化
1. 前言
这次,我们来聊一个轻松一点的话题,那就是给你一个矩阵A和一个矩阵B,使用矩阵乘法获得目标矩阵C,相信大家都不难写出下面的代码:
#define A( i, j ) a[ (i)*lda + (j) ]
#define B( i, j ) b[ (i)*ldb + (j) ]
#define C( i, j ) c[ (i)*ldc + (j) ]
// gemm C = A * B + C
void MatrixMultiply(int m, int n, int k, float *a, int lda, float *b, int ldb, float *c, int ldc)
{
for(int i = 0; i < m; i++){
for (int j=0; j for (int p=0; p C(i, j) = C(i, j) + A(i, p) * B(p, j);
}
}
}
}
然后,上篇文章如何判断算法是否有可优化空间?已经测了这段代码在单核A53(上篇文章错写为A17,十分抱歉)上的gflops表现,这种实现的gflops只有硬件的2%-3%,是十分低效的,因此这篇文章就是基于https://github.com/flame/how-to-optimize-gemm这个工程,给大家介绍一下矩阵乘法有哪些可以优化的方法。
需要注意的是,这个工程是针对X86上的列主序程序,我这里主要是在移动端A53上进行测试,所以将代码对应修改成了arm指令集,并且修改为更加常见的行主序进行测试。
原始版本的gFlops测试结果如下图所示:
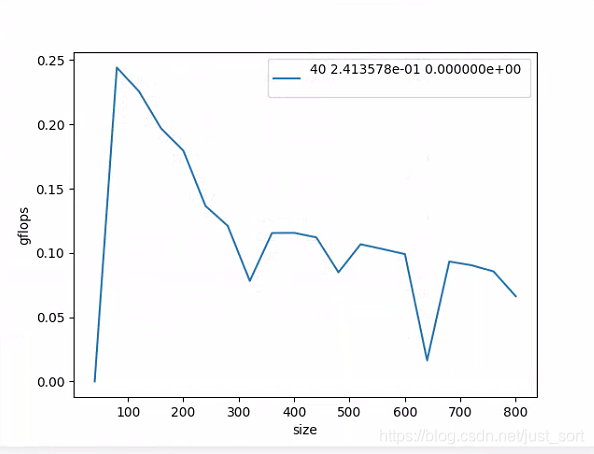
2. 优化之前的工作
在谈到优化之前,我们需要将前言中的那部分代码改成https://github.com/flame/how-to-optimize-gemm中类似的风格,这样便于对后面各种优化技巧代码的理解。改写风格后的代码如下:
#include
#define A( i, j ) a[ (i)*lda + (j) ]
#define B( i, j ) b[ (i)*ldb + (j) ]
#define C( i, j ) c[ (i)*ldc + (j) ]
/* Routine for computing C = A * B + C */
/* Create macro to let X( i ) equal the ith element of x */
#define Y(i) y[ (i)*incx ]
void AddDot( int k, float *x, int incx, float *y, float *gamma )
{
/* compute gamma := x' * y + gamma with vectors x and y of length n.
Here x starts at location x with increment (stride) incx and y starts at location y and has (implicit) stride of 1.
*/
int p;
for ( p=0; p *gamma += x[p] * Y(p);
}
}
void MY_MMult1( int m, int n, int k, float *a, int lda,
float *b, int ldb,
float *c, int ldc )
{
int i, j;
for ( j=0; j1 ){ /* Loop over the columns of C */
for ( i=0; i1 ){ /* Loop over the rows of C */
/* Update the C( i,j ) with the inner product of the ith row of A
and the jth column of B */
// for (int p=0; p
// C(i, j) = C(i, j) + A(i, p) * B(p, j);
// }
AddDot( k, &A( i,0 ), lda, &B( 0,j ), &C( i,j ) );
}
}
}
考虑到排版和篇幅的原因,后面的优化部分只贴最核心的代码,完整代码请到https://github.com/BBuf/ArmNeonOptimization查看,也欢迎Star这本项目。
3. 内存对齐
这里设计到Cache的概念,我尝试简短的描述一下,为什么内存对齐是对Cache命中有好处的。注意,内存对齐的原则是:任何K字节的基本对象的地址必须都是K的倍数。
Cache,译为高速缓冲存储器,它可以更好的利用局部性原理,减少CPU访问主存的次数。这里需要再简单描述一下计算机的存储体系,在当代计算中存储器是分为不同层次的,越靠近CPU的存储器速度越快,制造成本也就越高,同时容量也越小。最靠近CPU的存储器是寄存器,它的制造成本最高,所以个数也很有限。第二靠近的是缓存(Cache),同时缓存也是有分级的,有L1,L2,L3...等多个级别。再然后就是主存,即普通的内存。最后是本地磁盘。它们的容量以及访问时间如下图所示:
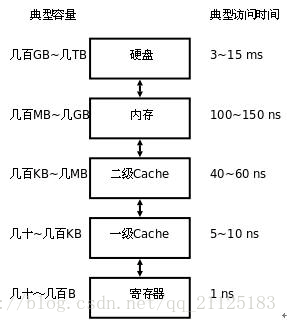
上面说Cache可以更好的利用局部性原理,所谓局部性原理就是优先从留CPU近的存储结构中去寻找当前需要查找的数据,加快数据访问速度从而减少程序中各个变量的存取时间。
关于Cache更多的概念可以参考一下文末的资料1,写得非常好。
“假设 cache line 为 32B。待访问数据大小为 64B,地址在 0x80000001,则需要占用 3 条 cache 映射表项;若地址在 0x80000000 则只需要 2 条。内存对齐变相地提高了 cache 命中率。” 假定kernel一次计算执行 大小的block, 根据MMult_4x4_7.c (https://github.com/flame/how-to-optimize-gemm/blob/master/src/MMult_4x4_7.c)和 MMult_4x4_8.c (https://github.com/flame/how-to-optimize-gemm/blob/master/src/MMult_4x4_8.c)代码,可以看出MMult_4x4_8.c使用了偏移量完成内存对齐。
这样我们就可以参考工程的MMult_1x4_3.c改写出一个FLOPs还不错的分块的矩阵乘法,代码实现如下,为了缩短代码长度,隐去了注释,如果有什么疑问欢迎留言区讨论:
void AddDot1x4( int k, float *a, int lda, float *b, int ldb, float *c, int ldc )
{
int p;
register float c_00_reg, c_01_reg, c_02_reg, c_03_reg, b_0p_reg;
float *ap0_pntr, *ap1_pntr, *ap2_pntr, *ap3_pntr;
ap0_pntr = &A( 0, 0 );
ap1_pntr = &A( 1, 0 );
ap2_pntr = &A( 2, 0 );
ap3_pntr = &A( 3, 0 );
c_00_reg = 0.0;
c_01_reg = 0.0;
c_02_reg = 0.0;
c_03_reg = 0.0;
for ( p=0; p4 ){
b_0p_reg = B( p, 0 );
c_00_reg += b_0p_reg * *ap0_pntr++;
c_01_reg += b_0p_reg * *ap1_pntr++;
c_02_reg += b_0p_reg * *ap2_pntr++;
c_03_reg += b_0p_reg * *ap3_pntr++;
b_0p_reg = B( p+1, 0 );
c_00_reg += b_0p_reg * *ap0_pntr++;
c_01_reg += b_0p_reg * *ap1_pntr++;
c_02_reg += b_0p_reg * *ap2_pntr++;
c_03_reg += b_0p_reg * *ap3_pntr++;
b_0p_reg = B( p+2, 0 );
c_00_reg += b_0p_reg * *ap0_pntr++;
c_01_reg += b_0p_reg * *ap1_pntr++;
c_02_reg += b_0p_reg * *ap2_pntr++;
c_03_reg += b_0p_reg * *ap3_pntr++;
b_0p_reg = B( p+3, 0 );
c_00_reg += b_0p_reg * *ap0_pntr++;
c_01_reg += b_0p_reg * *ap1_pntr++;
c_02_reg += b_0p_reg * *ap2_pntr++;
c_03_reg += b_0p_reg * *ap3_pntr++;
}
C( 0, 0 ) += c_00_reg;
C( 1, 0 ) += c_01_reg;
C( 2, 0 ) += c_02_reg;
C( 3, 0 ) += c_03_reg;
}
void MY_MMult_1x4_8( int m, int n, int k, float *a, int lda,
float *b, int ldb,
float *c, int ldc )
{
int i, j;
for ( j=0; j1 ){
for ( i=0; i4 ){
AddDot1x4( k, &A( i,0 ), lda, &B( 0,j ), ldb, &C( i,j ), ldc );
}
}
}
那么这个版本的gflops效果如何呢?单核A53测试结果如下:

可以看到最高的浮点峰值是原始版本的4倍,说明上面的优化是行之有效的。
接下来,我们将分块的策略从扩展到,代码实现如下:
void AddDot4x4( int k, float *a, int lda, float *b, int ldb, float *c, int ldc )
{
int p;
register float
c_00_reg, c_01_reg, c_02_reg, c_03_reg,
c_10_reg, c_11_reg, c_12_reg, c_13_reg,
c_20_reg, c_21_reg, c_22_reg, c_23_reg,
c_30_reg, c_31_reg, c_32_reg, c_33_reg,
a_0p_reg,
a_1p_reg,
a_2p_reg,
a_3p_reg,
b_p0_reg,
b_p1_reg,
b_p2_reg,
b_p3_reg;
float
/* Point to the current elements in the four rows of A */
*a_0p_pntr, *a_1p_pntr, *a_2p_pntr, *a_3p_pntr;
a_0p_pntr = &A( 0, 0);
a_1p_pntr = &A( 1, 0);
a_2p_pntr = &A( 2, 0);
a_3p_pntr = &A( 3, 0);
c_00_reg = 0.0; c_01_reg = 0.0; c_02_reg = 0.0; c_03_reg = 0.0;
c_10_reg = 0.0; c_11_reg = 0.0; c_12_reg = 0.0; c_13_reg = 0.0;
c_20_reg = 0.0; c_21_reg = 0.0; c_22_reg = 0.0; c_23_reg = 0.0;
c_30_reg = 0.0; c_31_reg = 0.0; c_32_reg = 0.0; c_33_reg = 0.0;
for ( p=0; p a_0p_reg = *a_0p_pntr++;
a_1p_reg = *a_1p_pntr++;
a_2p_reg = *a_2p_pntr++;
a_3p_reg = *a_3p_pntr++;
b_p0_reg = B( p, 0);
b_p1_reg = B( p, 1);
b_p2_reg = B( p, 2);
b_p3_reg = B( p, 3);
/* First row */
c_00_reg += a_0p_reg * b_p0_reg;
c_01_reg += a_0p_reg * b_p1_reg;
c_02_reg += a_0p_reg * b_p2_reg;
c_03_reg += a_0p_reg * b_p3_reg;
/* Second row */
c_10_reg += a_1p_reg * b_p0_reg;
c_11_reg += a_1p_reg * b_p1_reg;
c_12_reg += a_1p_reg * b_p2_reg;
c_13_reg += a_1p_reg * b_p3_reg;
/* Third row */
c_20_reg += a_2p_reg * b_p0_reg;
c_21_reg += a_2p_reg * b_p1_reg;
c_22_reg += a_2p_reg * b_p2_reg;
c_23_reg += a_2p_reg * b_p3_reg;
/* Four row */
c_30_reg += a_3p_reg * b_p0_reg;
c_31_reg += a_3p_reg * b_p1_reg;
c_32_reg += a_3p_reg * b_p2_reg;
c_33_reg += a_3p_reg * b_p3_reg;
}
C( 0, 0 ) += c_00_reg; C( 0, 1 ) += c_01_reg; C( 0, 2 ) += c_02_reg; C( 0, 3 ) += c_03_reg;
C( 1, 0 ) += c_10_reg; C( 1, 1 ) += c_11_reg; C( 1, 2 ) += c_12_reg; C( 1, 3 ) += c_13_reg;
C( 2, 0 ) += c_20_reg; C( 2, 1 ) += c_21_reg; C( 2, 2 ) += c_22_reg; C( 2, 3 ) += c_23_reg;
C( 3, 0 ) += c_30_reg; C( 3, 1 ) += c_31_reg; C( 3, 2 ) += c_32_reg; C( 3, 3 ) += c_33_reg;
}
然后再测一下gflops的表现:
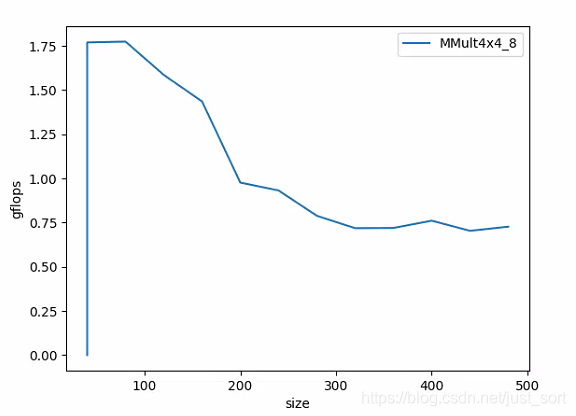
现在gflops提升到了1.75gflops,性能看起来好了不少,但是仍然存在随着矩阵尺寸快速变大性能衰减的问题,这个问题请看第六节。
4. 向量化SIMD
一个比较显然的优化是在k维度计算的时候可以使用Neon指令集进行优化,由于之前这个专栏中的文章已经讲得非常多了,这里不再赘述,贴一下在MMult_4x4_8版本基础上的核心修改部分:
void AddDot4x4( int k, float *a, int lda, float *b, int ldb, float *c, int ldc )
{
float
*a_0p_pntr, *a_1p_pntr, *a_2p_pntr, *a_3p_pntr;
a_0p_pntr = &A(0, 0);
a_1p_pntr = &A(1, 0);
a_2p_pntr = &A(2, 0);
a_3p_pntr = &A(3, 0);
float32x4_t c_p0_sum = {0};
float32x4_t c_p1_sum = {0};
float32x4_t c_p2_sum = {0};
float32x4_t c_p3_sum = {0};
register float
a_0p_reg,
a_1p_reg,
a_2p_reg,
a_3p_reg;
for (int p = 0; p < k; ++p) {
float32x4_t b_reg = vld1q_f32(&B(p, 0));
a_0p_reg = *a_0p_pntr++;
a_1p_reg = *a_1p_pntr++;
a_2p_reg = *a_2p_pntr++;
a_3p_reg = *a_3p_pntr++;
c_p0_sum = vmlaq_n_f32(c_p0_sum, b_reg, a_0p_reg);
c_p1_sum = vmlaq_n_f32(c_p1_sum, b_reg, a_1p_reg);
c_p2_sum = vmlaq_n_f32(c_p2_sum, b_reg, a_2p_reg);
c_p3_sum = vmlaq_n_f32(c_p3_sum, b_reg, a_3p_reg);
}
float *c_pntr = 0;
c_pntr = &C(0, 0);
float32x4_t c_reg = vld1q_f32(c_pntr);
c_reg = vaddq_f32(c_reg, c_p0_sum);
vst1q_f32(c_pntr, c_reg);
c_pntr = &C(1, 0);
c_reg = vld1q_f32(c_pntr);
c_reg = vaddq_f32(c_reg, c_p1_sum);
vst1q_f32(c_pntr, c_reg);
c_pntr = &C(2, 0);
c_reg = vld1q_f32(c_pntr);
c_reg = vaddq_f32(c_reg, c_p2_sum);
vst1q_f32(c_pntr, c_reg);
c_pntr = &C(3, 0);
c_reg = vld1q_f32(c_pntr);
c_reg = vaddq_f32(c_reg, c_p3_sum);
vst1q_f32(c_pntr, c_reg);
}
经过这个优化我们再测试一下当前版本(MMult_4x4_10)的gflops表现:

在矩阵长宽小于200时是有明显提升的,且最高的浮点峰值提升到了2.5gflops,说明这个优化在矩阵规模不大时是比较有用的。
5. 为什么需要分块&以及什么是分块?
前面的两个关键的优化在矩阵规模变大之后gflops就快速衰减,这是为什么呢?

这就和第3节讲到的计算机存储体系结构有关了,如Fig6所示。当我们的AB矩阵的大小比L2 Cache小时,我们的程序只需要从RAM中读取一次AB大小的内存,然后A,B矩阵的数据都可以被塞进Cache中。但是随着矩阵的大小增大,当AB矩阵的大小超过了L2 Cache时,由于行主序情况下的B矩阵或者列主序下的A矩阵不是内存连续的,那么程序就要从RAM读取多次AB矩阵的数据,这样数据存取将成为整个程序gflops上升的瓶颈。
因此,为了解决上一问题,gemm论文提出了矩阵分块的做法,直击核心,这篇论文针对矩阵乘法主要提出了下面6种不同的分块计算方法,如下图所示:

这个图中透漏了两个非常重要的点。
第一个是行主序下的A的一行乘以一列获得C的元素这个过程(A*B=C,其中A矩阵大小为,B矩阵大小为,C矩阵大小为)可以等价为A 的一列和 B 的一行操作得到 大小的一个 C 的“扇面”,多个“扇面”叠加就是完整的 C。所以这里的分块策略指的并不是在原始矩阵的长宽维度上分段计算,而是类似于一个z轴上拆分的思路,比较巧妙,所谓z轴就是垂直于矩阵长宽的维度。可以参考MMult_4x4_10的代码进行理解。
从MMult_4x4_10的结果来看,这个改进后的版本在矩阵规模变大时gflops也要好于之前的各个版本。另外为了验证上面的想法(当AB矩阵的大小超过了L2 Cache时,由于行主序情况下的B矩阵或者列主序下的A矩阵不是内存连续的,那么程序就要从RAM读取多次AB矩阵的数据,这样数据存取将成为整个程序gflops上升的瓶颈),我又做了一个对比试验,即在上面的z轴分块的版本下进一步对行列两个方向也进行分块,设置的步长和how-to-optimize-gemm一致,即:
#define mc 256
#define kc 128
void InnerKernel( int m, int n, int k, float *a, int lda,
float *b, int ldb,
float *c, int ldc )
{
int i, j;
for ( j=0; j4 ){ /* Loop over the columns of C, unrolled by 4 */
for ( i=0; i4 ){ /* Loop over the rows of C */
/* Update C( i,j ), C( i,j+1 ), C( i,j+2 ), and C( i,j+3 ) in
one routine (four inner products) */
AddDot4x4( k, &A( i,0 ), lda, &B(0, j), ldb, &C( i,j ), ldc );
}
}
}
void MY_MMult_4x4_11( int m, int n, int k, float *a, int lda,
float *b, int ldb,
float *c, int ldc )
{
int i, p, pb, ib;
for (p = 0; p < k; p += kc) {
pb = min(k - p, kc);
for (i = 0; i < m; i += mc) {
ib = min(m - i, mc);
InnerKernel(ib, n, pb, &A(i, p), lda, &B(p, 0), ldb, &C(i, 0), ldc);
}
}
}
然后我们再测一下这个版本(MMult_4x4_11)的gflops:

对比一下4x4_10的结果可以发现,在矩阵规模变大时,这个版本的gflops又好了不少,说明分块的确是利用Cache的一个好办法,毕竟Cache的容量是非常有限的。
在Figure4中透漏的第二个非常重要的点就是数据重排,也即数据Pack,之前我已经讲到2次这个技巧了,在这个矩阵乘法优化中同样适用。因为我们分块后的AB仍然是内存不连续的,为了提高内存的连续性,在做矩阵乘法之前先对A,B做了数据重排,将第二行要操作的数放在第一行的末尾,这样Neon中的数据预取指令将会生效,极大提高数据存取效率。基于这个想法获得了改进后的版本MMult_4x4_13.c,代码实现见:https://github.com/BBuf/ArmNeonOptimization/blob/master/optimize_gemm/MMult_4x4_13.h
测一下gflops:

可以看到相对于MMult_4x4_11 在矩阵规模变大时,这个版本的gflops提升明显,已经不会比这个版本的最高浮点峰值低太多了,说明这个优化是十分有效果的。
6. 总结
这篇文章讲到的优化方法都是有理论支撑的,也就是第5节展示的gemm论文中的那个Figure4。gemm论文我打算放到我后面的文章中进行解读,另外会再分享一些优化程度更大的算法,感兴趣的请关注一下我们的公众号,谢谢。
为了感谢读者朋友们的长期支持,我们今天将送出 3 本由北京大学出版社提供的《Python最优化算法实战》书籍,对本书感兴趣的可以在上方的留言区留言,我们将抽取其中三位读者送出一本正版书籍。

7. 参考
https://blog.csdn.net/qq_21125183/article/details/80590934 https://zhuanlan.zhihu.com/p/65436463 https://www.cs.utexas.edu/users/pingali/CS378/2008sp/papers/gotoPaper.pdf https://github.com/flame/how-to-optimize-gemm https://github.com/tpoisonooo/how-to-optimize-gemm
欢迎关注GiantPandaCV, 在这里你将看到独家的深度学习分享,坚持原创,每天分享我们学习到的新鲜知识。( • ̀ω•́ )✧
有对文章相关的问题,或者想要加入交流群,欢迎添加BBuf微信:
为了方便读者获取资料以及我们公众号的作者发布一些Github工程的更新,我们成立了一个QQ群,二维码如下,感兴趣可以加入。
