大佬是怎么优雅实现矩阵乘法的？-轻识

点击上方“视学算法”，选择加"星标"或“置顶”

重磅干货，第一时间送达

作者丨立交桥跳水冠军

来源丨https://zhuanlan.zhihu.com/p/383115932

转自丨极市平台

今天一翻朋友圈，发现好多人转发一个业内大佬写的开源项目。内容很简单，就是在CPU上实现单精度矩阵乘法。看了一下，结果非常好：CPU的利用率很高。更可贵的是核心代码只有很短不到200行。

之前总觉得自己很了解高性能计算，无外乎就是“局部性+向量”随便搞一搞。但是嘴上说说和实际实现自然有很大差别。看完了大佬的代码觉得受益匪浅，在这里总结了一下，当作自己的读书笔记了。

最前面自然是要放项目链接，强烈推荐大家读一读源代码：

https://github.com/pigirons/sgemm_hsw

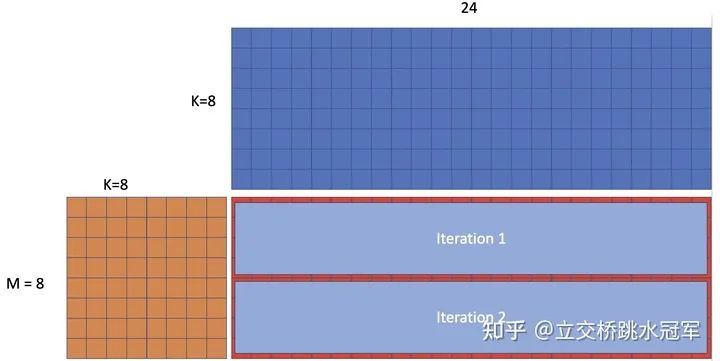
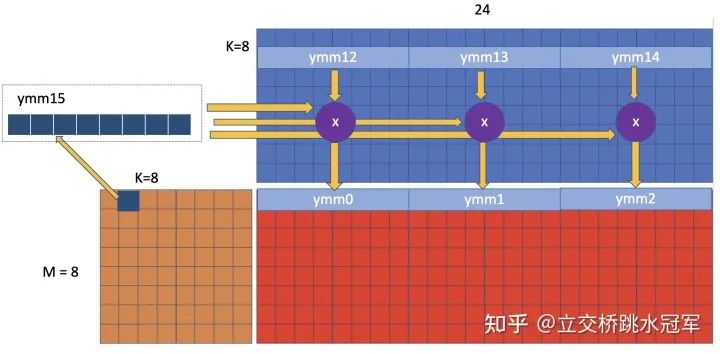
问题描述：给定两个矩阵，其shape分别为(m,k)和(k, 24),求矩阵相乘的结果。

为了方便理解，这里直接把m和k弄了一个数值带了进去。所以我们的问题如下：输入是棕色矩阵A和蓝色矩阵B，求红色矩阵C

我们知道一般矩阵乘法就是一堆循环的嵌套，这个也不例外。在代码里，最外层结果是输出矩阵的行遍历。又因为会有向量化的操作，所以最终结果是：最外层的循环每次算4行输出（PS：这里面的4是固定的，并不是我为了方便随便设的）。

就是下面的情况：

现在我们拆开来看每轮循环：我们每轮会算4行，24列的输出。在这里，我们把输出用12个向量寄存器表示。

现在可以隐约看出来为什么大佬要固定24这个数字了：因为ymm寄存器只有16个，我们又希望行数可以比较整，那么我们每次处理4行比较合适，处理4行的话，每行可以有16/4=4个寄存器。但是我们要做向量运算的话，那我们一定又要有向量寄存器当作运算符，所以我们不能把这16个寄存器都用来存output。所以权衡一下，那我们每行用3个寄存器好了，这样总共12个寄存器存结果，剩下4个用来搞搞计算。因为ymm是256bit的，可以存8个float类型，所以我们每列就应该是24

确定了计算的目标，下面我们继续更进一步，来看我们在每个内存循环都要做什么。还记得我们之前剩了4个ymm寄存器么？现在我们把它们都利用上：先来思考下我们能不能直接在A矩阵用ymm？如果用的话，那么我们会把A矩阵一行的连续数据存到一起。这些数据会和谁运算呢？是B的一列数据，也就是图中黑色的部分。一般来说我们假设矩阵都是列连续的。那么访问黑色的部分，locality就会很差：我们要把这些数字一个一个读出来，塞到一个ymm里面和A的ymm进行运算。

用排除法，我们别无选择，只能把ymm用到B上面。B也是24列，我们用3个ymm就存下了。还剩一个，我们先把A的第一行第一列的数字读出来，把它复制8份拓展成一个ymm，然后和这三个B的ymm作element-wise的乘法，把结果累加到ymm0~ymm2里。

现在发现这个算法的精妙了么？对的！他正好把16个ymm都用上了，一个不多一个不少

之后我们该干嘛？其实有很多选择，比如我们把ymm12~ymm14往下移动一行，和第一行第二列的数字做乘法，如下图：

（⚠️ 这个是低效的做法）

正确性上来说，上面的做法没问题。但我们来看看下图里大佬是怎么做的：

相比于之前我们说的循环到A的第一行第二列，大佬循环到了第二行第一列：在这种情况下我们只需要重新构造ymm15，原来的ymm12~ymm14完全都不需要变，不需要读新的数值，只需要改变输出位置，从原来写到ymm0~ymm2变成了ymm3~ymm5。但因为是写寄存器而非内存，所以都一样。

说到这儿，大概也把循环捋清楚了：最内层是按照A的列来迭代：（1）把A的第一行第一列读出来构造ymm15做计算，（2）把A的第二行第一列读出来构造ymm15做计算。。。。一直读到A的第四行第一列（为什么是第四行？因为我们输出是四行的寄存器），然后开始读A的第一行第二列构造ymm，然后读A的第二行第二列构造ymm。。。

总结：

（1）写并行计算，感觉就像在下国际象棋：你有很多种走法，这些走法都合法，但是最优的只有一种。

（2）实际上写高性能的程序就是在凑数：在这个代码里，我们根据体系结构里ymm的宽度和ymm的寄存器个数，推导出我们输出矩阵每行得有24列。然后又继续凑凑凑，得到了4步的步长的循环。虽然都是凑数，但是大佬的代码凑的很好：每一个ymm都被利用到了，这就是人家的水平。

点个在看 paper不断！