特征值和奇异值分解应用 - 典型相关分析 CCA 及 Python 实验-轻识

典型相关分析 (Canonical Correlation Analysis，CCA)，用于对来自同一样本的两个高维数据集作相关性分析的应用场景。一个经典的例子是来自同一个人的音频和视频数据集。也可以认为 CCA 是另一种降维技术，但与 PCA 不同的是在 CCA 会处理两个数据集。

1问题描述

现有两组随机变量，或者叫两个随机向量，以及，

包括个随机变量，

\mathbf{x}=[x_1,x_2,\cdots,x_r]

包含个随机变量，

\mathbf{y}=[y_1,y_2,\cdots,y_s]

在机器学习中，我们将一个随机变量看作特征，因此它们分别表示个特征和个特征。

现在需要分析两组特征之间的相关性。我们知道，如果都是单个特征，直接求相关系数即可，但因为有很多特征，不能直接求解相关系数。

当然这里也有其他的多元分析方法，但不妨先将和分别降到一维，得到两个新特征。降维可以分别降，比如两组分别求主成分，这自然是可以的，但是这样做的话两组特征之间独立处理，没有建立任何关联。因此，我们要求得到的这两个新特征之间的相关系数最大。

先不妨概括一下典型相关分析的重点，

CCA 用于联合处理两组特征集，其背后的目标是寻找一对投影，每组各一个，使得在投影后得到的新特征最大程度地相关。
把研究两组特征之间的问题化为研究两个所谓典型特征之间的相关问题。这里的典型特征不是从原特征组里挑出来的某个特征，而是原有特征的线性组合，因此需要求解的是这个线性组合的系数。

2问题求解

回到上面，两个随机向量以及，相应的观察值分别为，，。CCA 的目标就是求得一对方向，即，以便使得两组特征分别在这两方向上的投影值之间的相关性最大。设和是线性变换（投影）后的随机变量，已作零均值处理，相应的相关系数定义为

\rho_{\mathbf{z}_{x},\mathbf{z}_{y}}=\frac{\mathbf{E}\left[\mathbf{z}_{x} \mathbf{z}_{y}\right]}{\sqrt{\mathbf{E}\left[\mathbf{z}_{x}^{2}\right] \mathbf{E}\left[\mathbf{z}_{y}^{2}\right]}}=\frac{\mathbf{E}\left[\left({\bf w}_{x}^{\top} \mathbf{x}\right)\left(\mathbf{y}^{\top} {\bf w}_{y}\right)\right]}{\sqrt{\mathbf{E}\left[\left({\bf w}_{x}^{\top} \mathbf{x}\right)^{2}\right] \mathbf{E}\left[\left({\bf w}_{y}^{\top} \mathbf{y}\right)^{2}\right]}}

或者

\rho_{\mathbf{z}_{x},\mathbf{z}_{y}}=\frac{{\bf w}_{x}^{\top} \Sigma_{x y} {\bf w}_{y}}{\sqrt{\left({\bf w}_{x}^{\top} \Sigma_{x x} {\bf w}_{x}\right)\left({\bf w}_{y}^{\top} \Sigma_{y y} {\bf w}_{y}\right)}}

其中，

\left[\begin{array}{cc} \Sigma_{x x} & \Sigma_{x y} \\ \Sigma_{y x} & \Sigma_{y y} \end{array}\right] =\mathbf{E}\left( \left[\begin{array}{cc} \mathbf{x}\mathbf{x}^{\top} & \mathbf{x}\mathbf{y}^{\top} \\ \mathbf{y}\mathbf{x}^{\top} & \mathbf{y}\mathbf{y}^{\top} \end{array}\right]\right)

其中，。由于期望值并不知道，实际中我们用样本协方差代替总体协方差。此外，易知相关系数是关于尺度不变的。因此，求和以最大化相关系数等价于如下带约束的优化问题，

\begin{aligned} \max_{{\bf w}_{x}, {\bf w}_{y}} & \quad {\bf w}_{x}^{\top} {\Sigma}_{x y} {\bf w}_{y} \\[0.8em] \text { s.t. } & {\bf w}_{x}^{\top} {{\Sigma}}_{x x} {\bf w}_{x}=1 \\[0.5em] & {\bf w}_{y}^{\top} {{\Sigma}}_{y y} {\bf w}_{y}=1 \end{aligned}

CCA 的任务就是为两组特征分别计算两个投影方向，而约束是加权范数。CCA 关心两组特征分别在各自投影轴上的投影值（也可以理解成由已有特征的线性组合得到的新特征）之间的相关性。

+求特征值方法

为了求解上述优化问题，我们使用拉格朗日乘子法，

\begin{aligned} \mathcal{L}\left({\bf w}_{x}, {\bf w}_{y}, \lambda_{x}, \lambda_{y}\right) &={\bf w}_{x}^{\top} \Sigma_{x y} {\bf w}_{y}\\[1em] &-\frac{\lambda_{x}}{2}\left({\bf w}_{x}^{\top} \Sigma_{x x} {\bf w}_{x}-1\right)\\[1em] &-\frac{\lambda_{y}}{2}\left({\bf w}_{y}^{\top} \Sigma_{y y} {\bf w}_{y}-1\right) \end{aligned}

求关于和的梯度并等于零，得

\begin{aligned} {\Sigma}_{x y} {\bf w}_{y} &=\lambda_x \Sigma_{x x} {\bf w}_{x} \\[0.68em] \Sigma_{y x} {\bf w}_{x} &=\lambda_y \Sigma_{y y} {\bf w}_{y} \end{aligned}

由上面两式及约束条件易知，

\lambda_{x}=\lambda_{y}=\lambda

因此得，

\begin{aligned} {\Sigma}_{x y} {\bf w}_{y} &=\lambda \Sigma_{x x} {\bf w}_{x} \\[0.68em] \Sigma_{y x} {\bf w}_{x} &=\lambda \Sigma_{y y} {\bf w}_{y} \end{aligned}

假设和均可逆，则上面方程组的解为，

{\bf w}_{y}=\frac{1}{\lambda} {\Sigma}_{y y}^{-1} {\Sigma}_{y x} {\bf w}_{x}

其中，是矩阵的特征向量，即

\left({\Sigma}_{x x}^{-1} {\Sigma}_{x y} {\Sigma}_{y y}^{-1} {\Sigma}_{y x}\right) {\bf w}_{x}=\lambda^{2} {\bf w}_{x}

最后，待求相关系数的最优值为，

\rho={\bf w}_{x}^{\top} {\Sigma}_{x y} {\bf w}_{y}=\lambda {\bf w}_{x}^{\top} {\Sigma}_{x x} {\bf w}_{x}=\lambda

因此，选择最大特征值对应的特征向量作为投影方向，将得到最大相关系数。

+SVD 方法求解

该优化问题除了以上解法，还可以用 SVD 方法更简便地求解。我们回顾上面那个优化问题，

\begin{aligned} \max_{{\bf w}_{x}, {\bf w}_{y}} & \quad {\bf w}_{x}^{\top} {\Sigma}_{x y} {\bf w}_{y} \\[0.8em] \text { s.t. } & {\bf w}_{x}^{\top} {{\Sigma}}_{x x} {\bf w}_{x}=1 \\[0.5em] & {\bf w}_{y}^{\top} {{\Sigma}}_{y y} {\bf w}_{y}=1 \end{aligned}

引入如下变量代换，

{\bf u}_x = {\Sigma}_{x x}^{{1}/{2}}{\bf w}_x \Longrightarrow {\bf w}_x = {\Sigma}_{x x}^{{-1}/{2}}{\bf u}_x

以及，

{\bf u}_y = {\Sigma}_{y y}^{{1}/{2}}{\bf w}_y \Longrightarrow {\bf w}_y = {\Sigma}_{y y}^{{-1}/{2}}{\bf u}_y

代入优化问题，得如下形式，

\begin{aligned} \max_{{\bf u}_{x}, {\bf u}_{y}} & \quad {\bf u}_{x}^{\top} {\bf A}{\bf u}_{y} \\[0.8em] \text { s.t. } & {\bf u}_{x}^{\top} {\bf u}_{x}=1 \\[0.5em] & {\bf u}_{y}^{\top} {\bf u}_{y}=1 \end{aligned}

其中，

{\bf A} = {\Sigma}_{x x}^{{-1}/{2}}{\Sigma}_{x y} {\Sigma}_{y y}^{{-1}/{2}}

这个问题很眼熟，想起来没有。这可是 SVD 提出者之一法国数学家若尔当在引出奇异值分解时求解的优化问题。可以点击本号下面这篇重温一下那段历史。

万能的 SVD 分解是哪位牛人提出来的？

因此，我们只要计算

{\bf A} = {\Sigma}_{x x}^{{-1}/{2}}{\Sigma}_{x y} {\Sigma}_{y y}^{{-1}/{2}} = {{\bf U}_{\bf A} \Sigma_{\bf A}{\bf V}_{\bf A}}^{\top}

然后，拿出最大的奇异值以及对应的左奇异向量和右奇异向量，就得到解了，最后回代得到和。

特征向量被称为典型相关基向量，特征值被称为平方典型相关，投影量被称为典型变量。

+CCA 算法 SVD 求解步骤

输入：两组观察值和，

输出：两组数据的相关系数，投影方向和

计算各分量的协方差矩阵，各分量的协方差矩阵，和的互协方差矩阵，和的互协方差矩阵
计算矩阵
计算矩阵的奇异值分解，得到最大奇异值以及最大奇异值对应的左奇异向量和右奇异向量
计算和的投影向量和 , 得 ,

这里只用到了最大的奇异值，作为典型相关系数，实际上也可以像拿排在后面的奇异值以及奇异向量，得到第二相关系数、第三相关系数等。

+统一框架

CCA 其实还有很多兄弟姐妹，都可以联合处理不同数据集，只是在不同的需求和目标驱动下使用了不同的优化标准/约束。

实际上，可以在一个通用框架下描述其中一些方法。上面计算特征值 - 特征向量的问题可以合并在一起，即，

\mathtt{C} \bf{w} = \lambda \mathtt{B} \bf{w}

其中，

\bf{w} = [\bf{w}_{x}^{\top}, \bf{w}_{y}^{\top}]^{\top}

以及

\mathtt{C}=\left[\begin{array}{cc} \mathtt{O} & {\Sigma}_{x y} \\ {\Sigma}_{y x} & \mathtt{O} \end{array}\right], \quad \mathtt{B} = \left[\begin{array}{cc} {\Sigma}_{x x} & \mathtt{O} \\ \mathtt{O} & {\Sigma}_{y y} \end{array}\right]

通过调整矩阵和，我们可以得到不同的方法。比如令以及，就得到求解 PCA 的特征值 - 特征向量任务。

{\Sigma}_{x x} \bf{w} = \lambda \bf{w}

CCA 算法依赖于数据的线性表示，如果数据并不是线性的，那就使用核函数将数据映射到高维，然后再用 CCA 降维，即所谓的核-CCA。

3Python 实验

我们准备那 seaborn 里提供的一个企鹅种类数据集来演示 CCA。

import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt

data = "https://raw.githubusercontent.com/mwaskom/seaborn-data/master/penguins.csv"

df = pd.read_csv(data)
df = df.dropna()
df.head()

对于特征的意义，请对照下图理解。

# 喙

X = df[['bill_length_mm','bill_depth_mm']]
X.head()

# 对数据作标准化处理

X_mc = (X-X.mean())/(X.std())
X_mc.head()

Y = df[['flipper_length_mm','body_mass_g']]
Y_mc = (Y-Y.mean())/(Y.std())
Y_mc.head()

from sklearn.cross_decomposition import CCA

cca = CCA(n_components=2)
cca.fit(X_mc, Y_mc)
X_c, Y_c = cca.transform(X_mc, Y_mc)

scores = np.corrcoef(cca.x_scores_, cca.y_scores_, rowvar=False)
score = np.diag(scores[:2, 2:])
score

array([0.78763151, 0.08638695])

现在我们已经完成了典型相关分析，让我们更深入地了解我们作为结果得到的典型协变量对。

在这个玩具示例中，我们知道我们拥有的两组度量值，因为这两个数据矩阵来自同一组企鹅。我们早些时候怀疑这些测量的差异是由于企鹅物种差异造成的。因此，这两个测量值背后的一个共同潜在变量是物种变量。而我们的 CCA 分析的主要目标是捕捉共同变量。我们还看到第一对规范变量高度相关。

让我们检验一下典型协变量是否实际上是种类变量。首先，让我们用企鹅数据和第一对典型协变量创建数据矩阵。

cc_res = pd.DataFrame({"CCX_1":X_c[:, 0],
                       "CCY_1":Y_c[:, 0],
                       "CCX_2":X_c[:, 1],
                       "CCY_2":Y_c[:, 1],
                       "Species":df.species.tolist(),
                       "Island":df.island.tolist(),
                       "sex":df.sex.tolist()})

cc_res.head()

为了查看每个典型变量是否与企鹅数据集中的种类变量相关，我们使用典型协变量和种类变量绘制一个箱线图。

plt.figure(figsize=(10, 6))
sns.boxplot(x="Species",
            y="CCX_1", 
            data=cc_res)
sns.stripplot(x="Species",
              y="CCX_1", 
              data=cc_res)

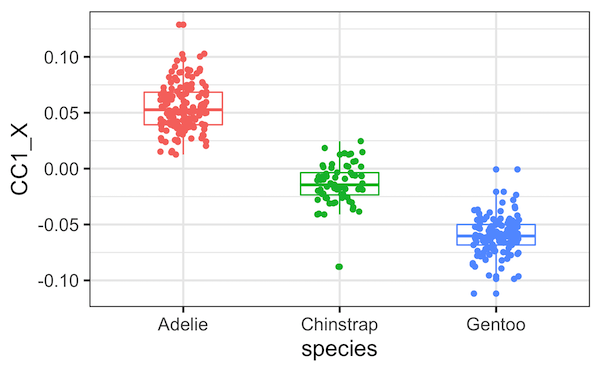
从箱线图中可以清楚地看出，第一对典型协变量确实与种类变量高度相关。

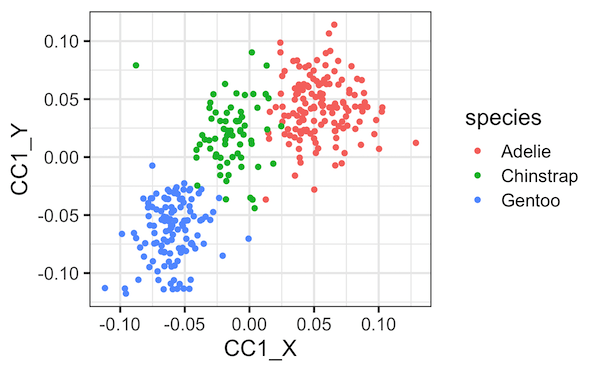
最后，再将两个典型协变量一起绘制，以种类变量着色，将更清楚地揭示种类与两个典型协变量之间的关系。

plt.figure(figsize=(10,6))
sns.scatterplot(x="CCX_1",
                y="CCY_1", 
                hue="Species", data=cc_res)
plt.title('First Pair of Canonical Covariate, corr = %.2f' %
         np.corrcoef(X_c[:, 0], Y_c[:, 0])[0, 1])

Text(0.5, 1.0, 'First Pair of Canonical Covariate, corr = 0.79')

相关阅读

万能的 SVD 分解是哪位牛人提出来的？