独家|OpenCV 1.7 离散傅里叶变换
翻译:陈之炎 校对:李海明
本文约2400字,建议阅读5分钟
本文为大家介绍了OpenCV离散傅里叶变换。
目标
什么是傅立叶变换,为什么要使用傅立叶变换?
如何在OpenCV中使用傅立叶变换?
copyMakeBorder() , merge() , dft() , getOptimalDFTSize() , log() 和 normalize() 等函数的使用方法。
源代码
可以到
samples/cpp/tutorial_code/core/discrete_fourier_transform/discrete_fourier_transform.cpp目录下查看OpenCV的源代码库。
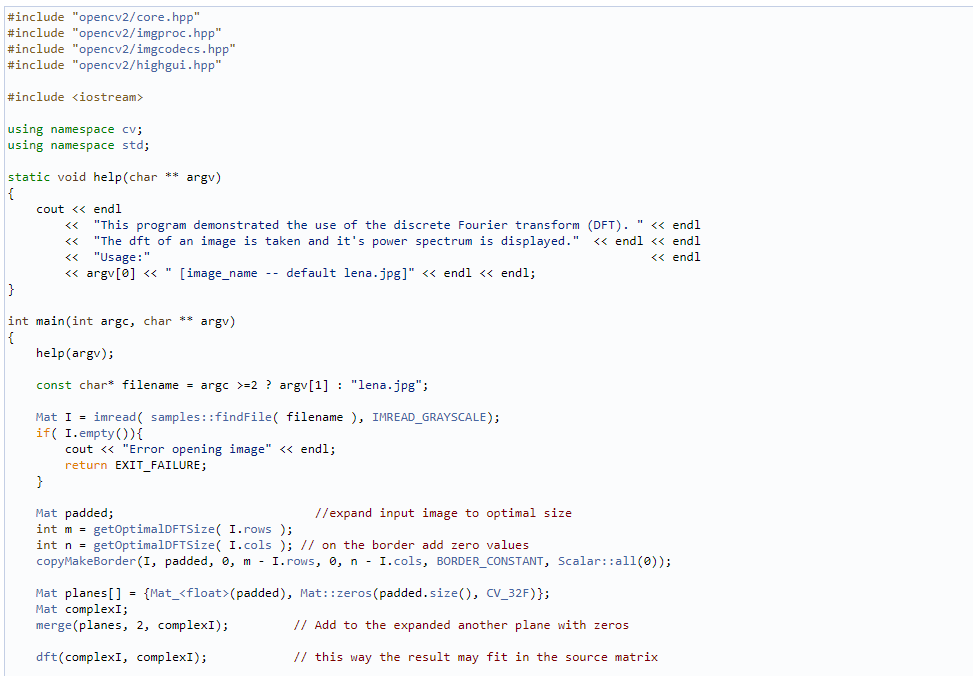
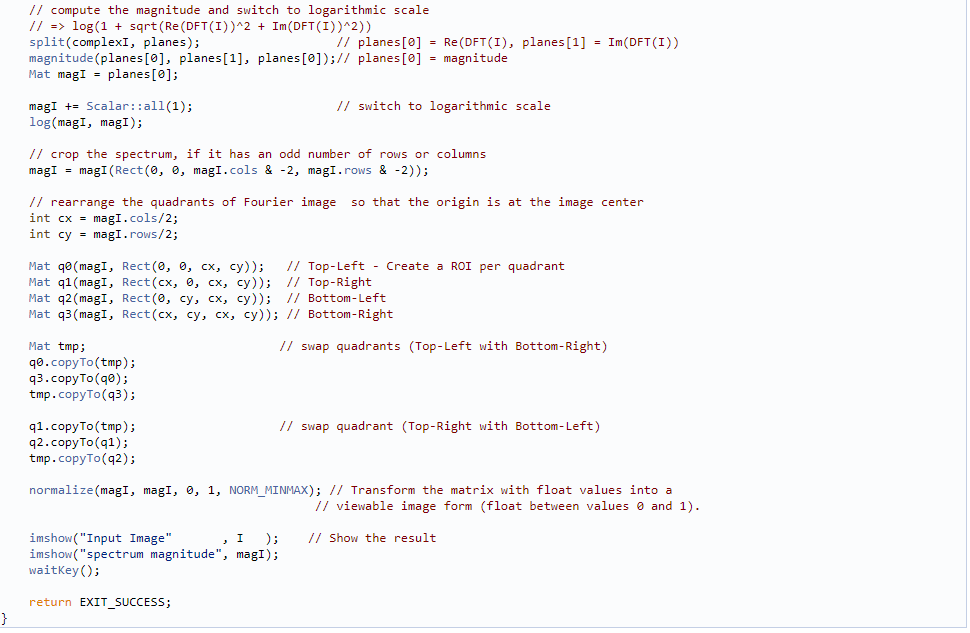
代码详解
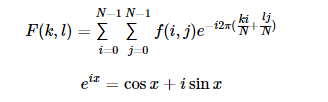
将图像展开到最佳尺寸
DFT的性能取决于图像的大小,当图像的尺寸为2,3,5 的倍数时,离散傅里叶变换(DFT )的速度最快。因此,为获得最优的性能,可以通过调整图像的边界值来获得便于快速计算的图像尺寸。getOptimalDFTSize()函数返回一个最优尺寸的图像,使用copyMakeBorder()函数扩展图像(将增加的像素值初始化为零)的边界:

为复数的实部和虚部开辟存储空间

离散傅立叶变换
进行原位计算(输入数据同输出数据):

将复数的实部和虚部转换成幅度值
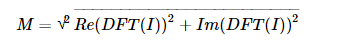

切换到对数尺寸
由于傅里叶系数的动态范围过大,无法在屏幕上显示,
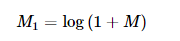

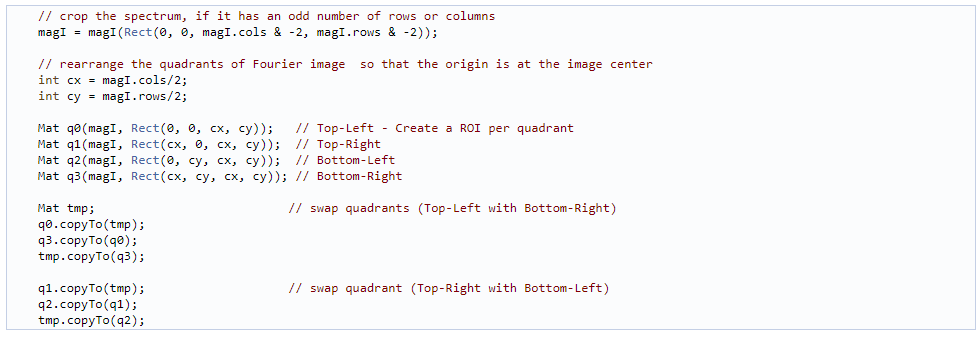
剪裁和重排
归一化

结果


https://docs.opencv.org/4.5.2/d8/d01/tutorial_discrete_fourier_transform.html
独家|OpenCV 1.2 如何用OpenCV扫描图像、查找表和测量时间(附链接)
独家|OpenCV 1.4 对图像的操作
译者简介
陈之炎,北京交通大学通信与控制工程专业毕业,获得工学硕士学位,历任长城计算机软件与系统公司工程师,大唐微电子公司工程师,现任北京吾译超群科技有限公司技术支持。目前从事智能化翻译教学系统的运营和维护,在人工智能深度学习和自然语言处理(NLP)方面积累有一定的经验。业余时间喜爱翻译创作,翻译作品主要有:IEC-ISO 7816、伊拉克石油工程项目、新财税主义宣言等等,其中中译英作品“新财税主义宣言”在GLOBAL TIMES正式发表。能够利用业余时间加入到THU 数据派平台的翻译志愿者小组,希望能和大家一起交流分享,共同进步
翻译组招募信息
工作内容:需要一颗细致的心,将选取好的外文文章翻译成流畅的中文。如果你是数据科学/统计学/计算机类的留学生,或在海外从事相关工作,或对自己外语水平有信心的朋友欢迎加入翻译小组。
你能得到:定期的翻译培训提高志愿者的翻译水平,提高对于数据科学前沿的认知,海外的朋友可以和国内技术应用发展保持联系,THU数据派产学研的背景为志愿者带来好的发展机遇。
其他福利:来自于名企的数据科学工作者,北大清华以及海外等名校学生他们都将成为你在翻译小组的伙伴。
点击文末“阅读原文”加入数据派团队~
转载须知
如需转载,请在开篇显著位置注明作者和出处(转自:数据派ID:DatapiTHU),并在文章结尾放置数据派醒目二维码。有原创标识文章,请发送【文章名称-待授权公众号名称及ID】至联系邮箱,申请白名单授权并按要求编辑。
发布后请将链接反馈至联系邮箱(见下方)。未经许可的转载以及改编者,我们将依法追究其法律责任。
点击“阅读原文”拥抱组织


