神了 BitMap !

作者 | 废物大师兄
1. BitMap
Bit-map的基本思想就是用一个bit位来标记某个元素对应的Value,而Key即是该元素。由于采用了Bit为单位来存储数据,因此在存储空间方面,可以大大节省。(PS:划重点 节省存储空间)
假设有这样一个需求:在20亿个随机整数中找出某个数m是否存在其中,并假设32位操作系统,4G内存
在Java中,int占4字节,1字节=8位(1 byte = 8 bit)
如果每个数字用int存储,那就是20亿个int,因而占用的空间约为 (2000000000*4/1024/1024/1024)≈7.45G
如果按位存储就不一样了,20亿个数就是20亿位,占用空间约为 (2000000000/8/1024/1024/1024)≈0.233G
高下立判,无需多言
那么,问题来了,如何表示一个数呢?
刚才说了,每一位表示一个数,0表示不存在,1表示存在,这正符合二进制
这样我们可以很容易表示{1,2,4,6}这几个数:

当然是在另一个8位上表示了:
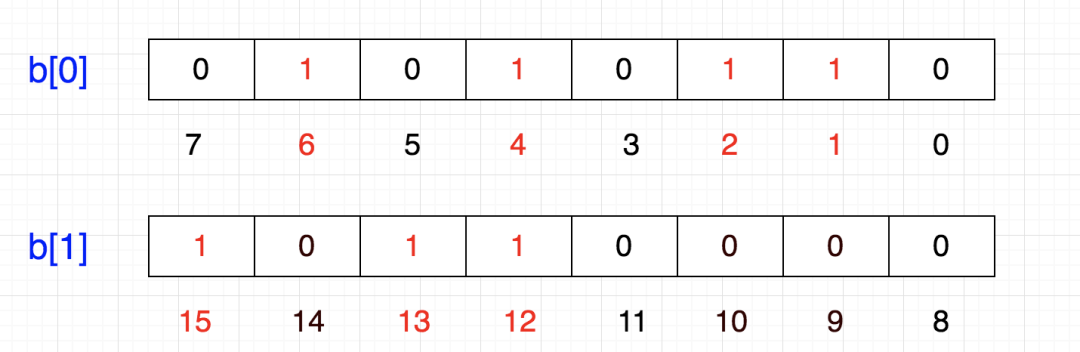
这样的话,好像变成一个二维数组了
1个int占32位,那么我们只需要申请一个int数组长度为 int tmp[1+N/32] 即可存储,其中N表示要存储的这些数中的最大值,于是乎:
tmp[0]:可以表示0~31
tmp[1]:可以表示32~63
tmp[2]:可以表示64~95
。。。
如此一来,给定任意整数M,那么M/32就得到下标,M%32就知道它在此下标的哪个位置
添加
这里有个问题,我们怎么把一个数放进去呢?例如,想把5这个数字放进去,怎么做呢?
首先,5/32=0,5%32=5,也是说它应该在tmp[0]的第5个位置,那我们把1向左移动5位,然后按位或
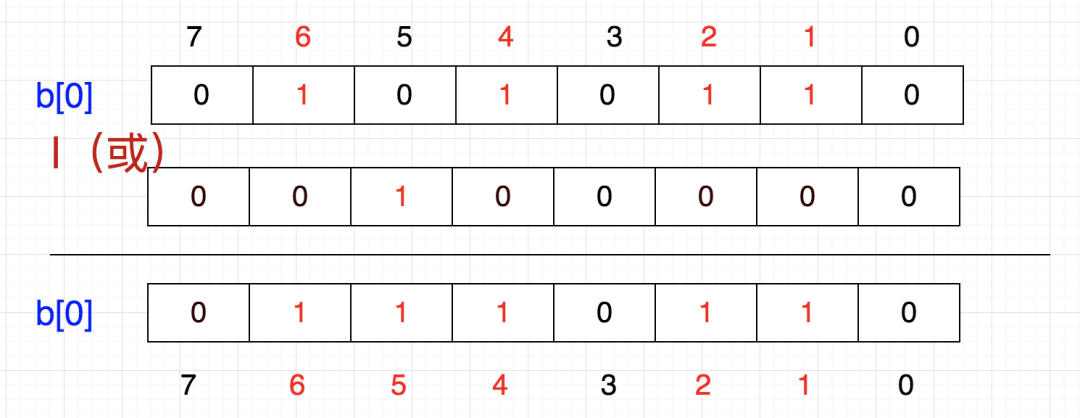
换成二进制就是

这就相当于 86 | 32 = 118
86 | (1<<5) = 118
b[0] = b[0] | (1<<5)
也就是说,要想插入一个数,将1左移带代表该数字的那一位,然后与原数进行按位或操作
化简一下,就是 86 + (5/8) | (1<<(5%8))
因此,公式可以概括为:p + (i/8)|(1<<(i%8)) 其中,p表示现在的值,i表示待插入的数
清除
以上是添加,那如果要清除该怎么做呢?
还是上面的例子,假设我们要6移除,该怎么做呢?
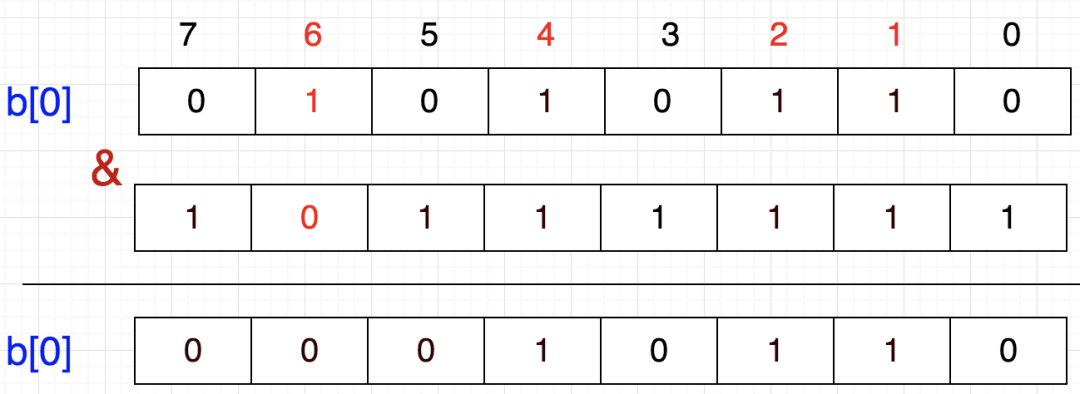
从图上看,只需将该数所在的位置为0即可
1左移6位,就到达6这个数字所代表的位,然后按位取反,最后与原数按位与,这样就把该位置为0了
b[0] = b[0] & (~(1<<6))
b[0] = b[0] & (~(1<<(i%8)))
查找
前面我们也说了,每一位代表一个数字,1表示有(或者说存在),0表示无(或者说不存在)。通过把该为置为1或者0来达到添加和清除的小伙,那么判断一个数存不存在就是判断该数所在的位是0还是1
假设,我们想知道3在不在,那么只需判断 b[0] & (1<<3) 如果这个值是0,则不存在,如果是1,就表示存在
2. Bitmap有什么用
大量数据的快速排序、查找、去重
快速排序
假设我们要对0-7内的5个元素(4,7,2,5,3)排序(这里假设这些元素没有重复),我们就可以采用Bit-map的方法来达到排序的目的。
要表示8个数,我们就只需要8个Bit(1Bytes),首先我们开辟1Byte的空间,将这些空间的所有Bit位都置为0,然后将对应位置为1。
最后,遍历一遍Bit区域,将该位是一的位的编号输出(2,3,4,5,7),这样就达到了排序的目的,时间复杂度O(n)。
优点:
运算效率高,不需要进行比较和移位; 占用内存少,比如N=10000000;只需占用内存为N/8=1250000Byte=1.25M
缺点:
所有的数据不能重复。即不可对重复的数据进行排序和查找。 只有当数据比较密集时才有优势
快速去重
20亿个整数中找出不重复的整数的个数,内存不足以容纳这20亿个整数。
首先,根据“内存空间不足以容纳这05亿个整数”我们可以快速的联想到Bit-map。下边关键的问题就是怎么设计我们的Bit-map来表示这20亿个数字的状态了。其实这个问题很简单,一个数字的状态只有三种,分别为不存在,只有一个,有重复。因此,我们只需要2bits就可以对一个数字的状态进行存储了,假设我们设定一个数字不存在为00,存在一次01,存在两次及其以上为11。那我们大概需要存储空间2G左右。
接下来的任务就是把这20亿个数字放进去(存储),如果对应的状态位为00,则将其变为01,表示存在一次;如果对应的状态位为01,则将其变为11,表示已经有一个了,即出现多次;如果为11,则对应的状态位保持不变,仍表示出现多次。
最后,统计状态位为01的个数,就得到了不重复的数字个数,时间复杂度为O(n)。
快速查找
这就是我们前面所说的了,int数组中的一个元素是4字节占32位,那么除以32就知道元素的下标,对32求余数(%32)就知道它在哪一位,如果该位是1,则表示存在。
小结&回顾
Bitmap主要用于快速检索关键字状态,通常要求关键字是一个连续的序列(或者关键字是一个连续序列中的大部分), 最基本的情况,使用1bit表示一个关键字的状态(可标示两种状态),但根据需要也可以使用2bit(表示4种状态),3bit(表示8种状态)。
Bitmap的主要应用场合:表示连续(或接近连续,即大部分会出现)的关键字序列的状态(状态数/关键字个数 越小越好)。
32位机器上,对于一个整型数,比如int a=1 在内存中占32bit位,这是为了方便计算机的运算。但是对于某些应用场景而言,这属于一种巨大的浪费,因为我们可以用对应的32bit位对应存储十进制的0-31个数,而这就是Bit-map的基本思想。Bit-map算法利用这种思想处理大量数据的排序、查询以及去重。
补充1
在数字没有溢出的前提下,对于正数和负数,左移一位都相当于乘以2的1次方,左移n位就相当于乘以2的n次方,右移一位相当于除2,右移n位相当于除以2的n次方。
<< 左移,相当于乘以2的n次方,例如:1<<6 相当于1×64=64,3<<4 相当于3×16=48
>> 右移,相当于除以2的n次方,例如:64>>3 相当于64÷8=8
^ 异或,相当于求余数,例如:48^32 相当于 48%32=16
补充2
不使用第三方变量,交换两个变量的值
1 // 方式一
2 a = a + b;
3 b = a - b;
4 a = a - b;
5
6 // 方式二
7 a = a ^ b;
8 b = a ^ b;
9 a = a ^ b;
3. BitSet
BitSet实现了一个位向量,它可以根据需要增长。每一位都有一个布尔值。一个BitSet的位可以被非负整数索引(PS:意思就是每一位都可以表示一个非负整数)。可以查找、设置、清除某一位。通过逻辑运算符可以修改另一个BitSet的内容。默认情况下,所有的位都有一个默认值false。
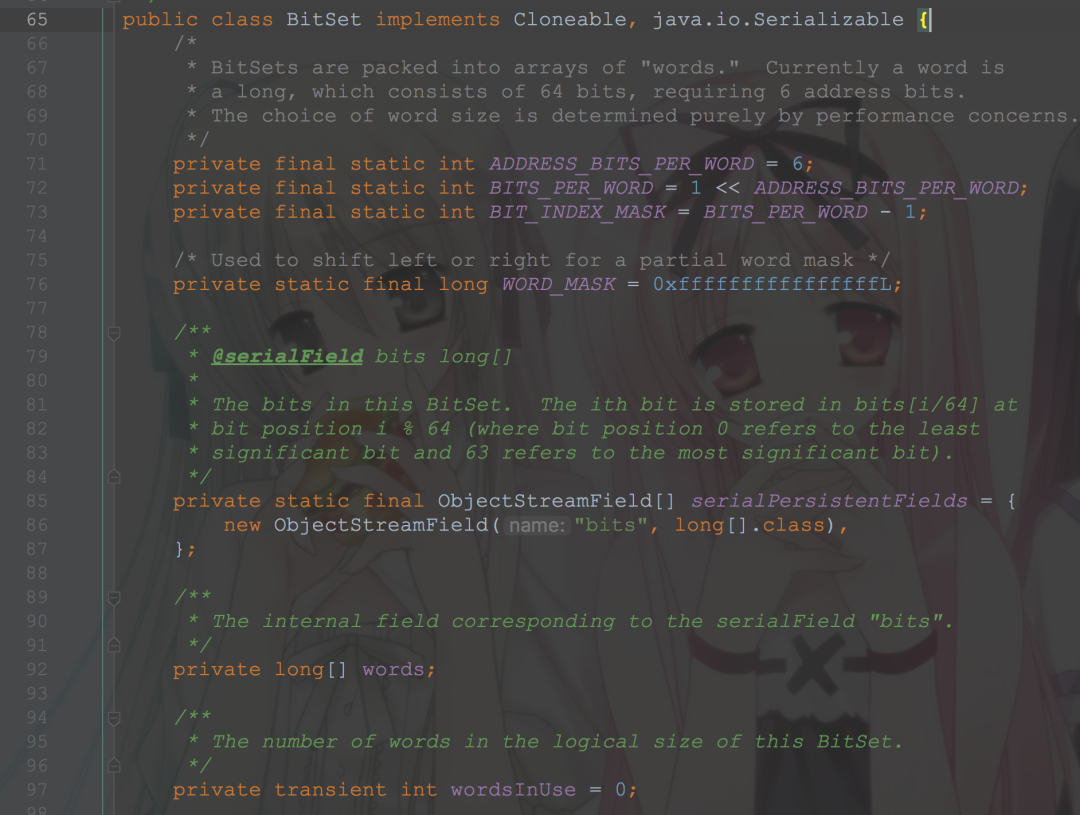

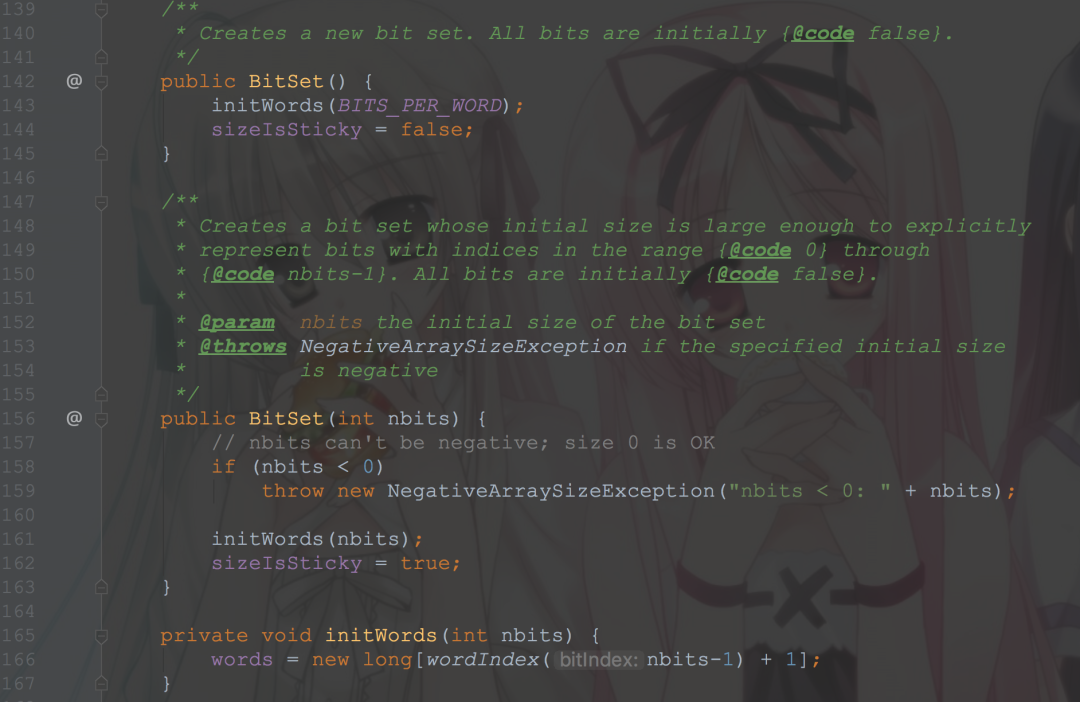
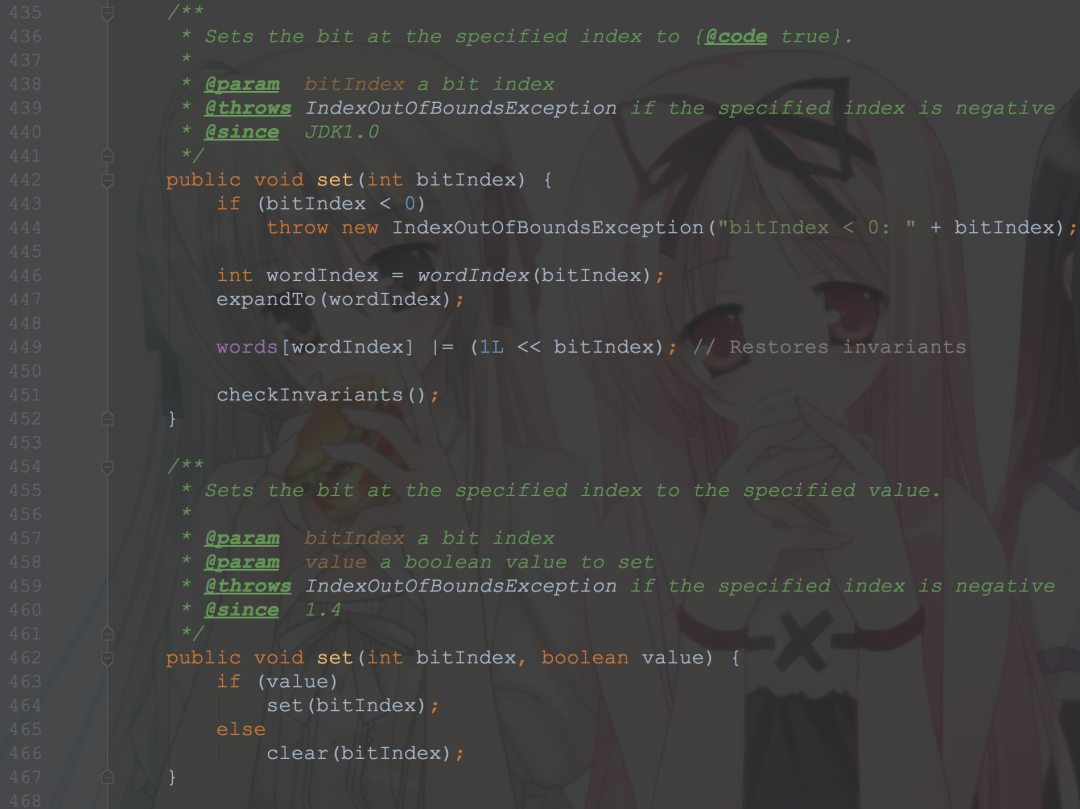
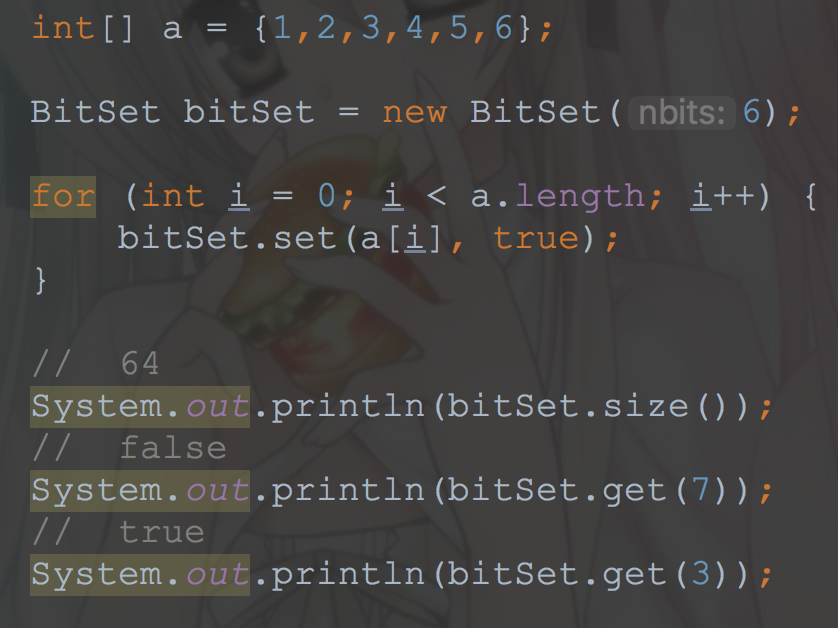
可以看到,跟我们前面想的差不多
用一个long数组来存储,初始长度64,set值的时候首先右移6位(相当于除以64)计算在数组的什么位置,然后更改状态位
别的看不懂不要紧,看懂这两句就够了:
1 int wordIndex = wordIndex(bitIndex);
2 words[wordIndex] |= (1L << bitIndex);
4. Bloom Filters
Bloom filter 是一个数据结构,它可以用来判断某个元素是否在集合内,具有运行快速,内存占用小的特点。
而高效插入和查询的代价就是,Bloom Filter 是一个基于概率的数据结构:它只能告诉我们一个元素绝对不在集合内或可能在集合内。
Bloom filter 的基础数据结构是一个 比特向量(可理解为数组)。
主要应用于大规模数据下不需要精确过滤的场景,如检查垃圾邮件地址,爬虫URL地址去重,解决缓存穿透问题等
如果想判断一个元素是不是在一个集合里,一般想到的是将集合中所有元素保存起来,然后通过比较确定。链表、树、散列表(哈希表)等等数据结构都是这种思路,但是随着集合中元素的增加,需要的存储空间越来越大;同时检索速度也越来越慢,检索时间复杂度分别是O(n)、O(log n)、O(1)。
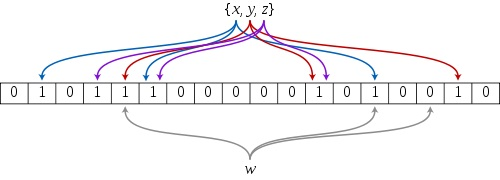
布隆过滤器的原理是,当一个元素被加入集合时,通过 K 个散列函数将这个元素映射成一个位数组(Bit array)中的 K 个点,把它们置为 1 。检索时,只要看看这些点是不是都是1就知道元素是否在集合中;如果这些点有任何一个 0,则被检元素一定不在;如果都是1,则被检元素很可能在(之所以说“可能”是误差的存在)。
BloomFilter 流程
首先需要 k 个 hash 函数,每个函数可以把 key 散列成为 1 个整数; 初始化时,需要一个长度为 n 比特的数组,每个比特位初始化为 0; 某个 key 加入集合时,用 k 个 hash 函数计算出 k 个散列值,并把数组中对应的比特位置为 1; 判断某个 key 是否在集合时,用 k 个 hash 函数计算出 k 个散列值,并查询数组中对应的比特位,如果所有的比特位都是1,认为在集合中。
1 <dependency>
2 <groupId>com.google.guava</groupId>
3 <artifactId>guava</artifactId>
4 <version>28.1-jre</version>
5 </dependency>
