七十八、 回溯法解决八皇后问题
「@Author:Runsen」
八皇后问题
「八皇后问题」是一个以国际象棋为背景的问题:如何能够在8×8的国际象棋棋盘上放置八个皇后,使得任何一个皇后都无法直接吃掉其他的皇后。
来自百度百科,皇后的走法是可以横竖斜着走任意格。
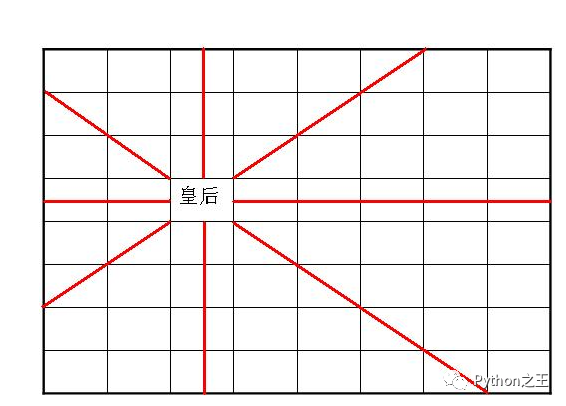
国际象棋棋盘是8 * 8的方格,每个方格里放一个棋子。皇后这种棋子可以攻击同一行或者同一列或者斜线(左上左下右上右下四个方向)上的棋子。在一个棋盘上如果要放八个皇后,使得她们互相之间不能攻击(即任意两两之间都不同行不同列不同斜线),求出一种所有布局方式。
八皇后问题,是一个古老而著名的问题,是经典又脍炙人口的典型编程问题。该问题是国际西洋棋棋手马克斯·贝瑟尔于1848年提出:在8×8格的国际象棋上摆放八个皇后,使其不能互相攻击,即任意两个皇后都不能处于同一行、同一列或同一斜线上,问有多少种摆法。高斯认为有76种方案。
1854年在柏林的象棋杂志上不同的作者发表了40种不同的解,后来有人用图论的方法解出92种结果。计算机发明后,计算机语言可以解决此问题。
好了我们来解决这个八皇后的问题,下面介绍是回溯法
回溯法
回溯法(探索与回溯法)是一种选优搜索法,又称为试探法,按选优条件向前搜索,以达到目标。但当探索到某一步时,发现原先选择并不优或达不到目标,就退回一步重新选择,这种走不通就退回再走的技术为回溯法,而满足回溯条件]的某个状态的点称为“回溯点”。(来自百度百科)
说到底,就是一个一个的试错,在第一行第一个列放皇后,然后在第二行放皇后,一直将整个棋盘放满。如果发现放不了,就回到上一行放皇后的地方,选择其他位置放皇后。
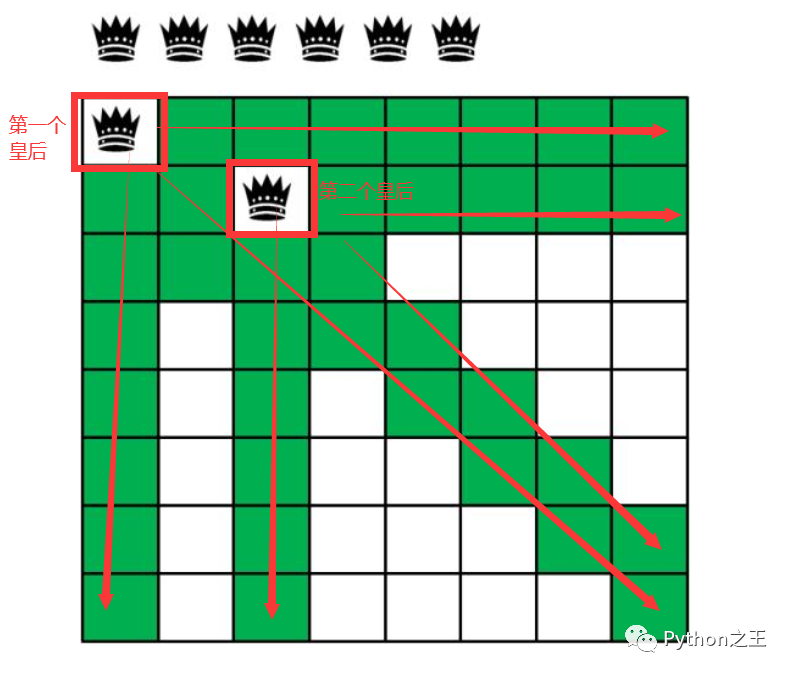
回溯法就是不断的试错,有错了就回到上一行放皇后,直到整个棋盘放满。
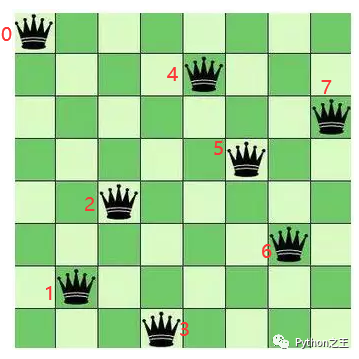
下图是八皇后问题的一个解:

首先定义一个冲突函数,如下,ps是positions 的缩写,表示之前摆放的皇后位置,是一个list,每个元素代表第几列放的,比如上图所有的皇后可以表示为
[0,4,7,5,2,6,1,3]
state 这里理解元组,就是之前放回皇后的位置,nextX表示新皇后要放的横坐标,conflict函数就是检测新皇后放的位置和之前的皇后在位置上是否有冲突,有的话返回True。
def conflict(state, nextX):
nextY = len(state)
# 新皇后要放的纵坐标
# print(state) #不知道可以下面打印下
for i in range(nextY):
#在同一行或者在对角线上 nextY-i=1 就是对角线
if abs(state[i]-nextX) in (0, nextY-i):
return True
return False
再定义一个queens函数, 这里我们用Python的生成器来存储我们的结果
def queens(num,state=()):
for pos in range(num):
# 没有冲突
if not conflict(state,pos):
# 最后一个pos,就是放到了最后一行,就yield储存在queens队列中
if len(state) ==num-1:
yield(pos,)
# 还没有到最后一行,就放皇后
else:
# 遍历之前的queens队列中储存的结果,(pos,) 就是当前放皇后,我们不知道是否最后一行,所以不断地递归,直到放到了最后一行
for result in queens(num, state + (pos,)):
yield (pos, ) + result
print(len(list(queens(8))))
# 92
一共有92中方法

list(queens(8))就是我们的结果,下面我们定义一个preetyprint打印美观先
import random
def preetyprint(solution): # pilish 输出
def line(pos, length=len(solution)):
return '| '*(pos)+'|X'+'| '*(length-pos)
for pos in solution:
print (line(pos))
preetyprint(random.choice(list(queens(8))))
| | | | | | |X| |
| | | |X| | | | |
| |X| | | | | | |
| | | | | | | |X|
| | | | | |X| | |
|X| | | | | | | |
| | |X| | | | | |
| | | | |X| | | |
完整代码
整个代码中包含了三个方法,分别是conflict、queens、preetyprint。
import random
def conflict(state, nextX):
nextY = len(state)
# 新皇后要放的纵坐标
# print(state) #不知道可以下面打印下
for i in range(nextY):
#在同一行或者在对角线上 nextY-i=1 就是对角线
if abs(state[i]-nextX) in (0, nextY-i):
return True
return False
def queens(num,state=()):
for pos in range(num):
# 没有冲突
if not conflict(state,pos):
# 最后一个pos,就是放到了最后一行,就yield储存在queens队列中
if len(state) ==num-1:
yield(pos,)
# 还没有到最后一行,就放皇后
else:
# 遍历之前的queens队列中储存的结果,(pos,) 就是当前放皇后,我们不知道是否最后一行,所以不断地递归,直到放到了最后一行
for result in queens(num, state + (pos,)):
yield (pos, ) + result
def preetyprint(solution):
def line(pos, length=len(solution)):
return '| '*(pos)+'|X'+'| '*(length-pos)
for pos in solution:
print (line(pos))
print(len(list(queens(8))))
preetyprint(random.choice(list(queens(8))))
for i in list(queens(8)):
print(i)
❝本文已收录 GitHub,传送门~[1] ,里面更有大厂面试完整考点,欢迎 Star。
❞
Reference
传送门~: https://github.com/MaoliRUNsen/runsenlearnpy100
更多的文章
点击下面小程序
- END -

