【SU Ruby教程】图元定义(5):表面

本篇教程继续介绍另一种概念性图元( conceptual entity )——表面。与上一篇教程相同,文中的示例可能会使用到本人自制的 Sel 模块,在注释中会解释相应语句的作用,测试时可以自行替换等价的表达。当然也可以直接参考此篇文章 [SU-2021-05],下载和使用此模块。
图元定义(5):表面
| 【本期目录】 | |
| (1)表面的特性 ①表面的本质 ②表面的选择 ③一些特性 | (3)表面的空间计算 ①点在表面上的投影 ②表面限制下落 |
(2)表面的创建 ①软化边线 ②通过曲线创建 ③PolygonMesh | (4)空间网 Mesh ①Geom:: PolygonMesh ②Mesh 的获取方式 ③Mesh 的用途 |
(1)表面的特性
①表面的本质
作为概念性图元,表面本身同样不是继承自 Drawingelement 类的实例,甚至也不像曲线那样,拥有继承自 Entity 类的 Curve 或 ArcCurve。这是因为表面的复杂程度和自由程度远远甚于曲线,很难用一个有序端点列表或者是诸如半径、法向量等这些属性来记录,因此也就没有必要单独设计一个描述表面图元的类了。
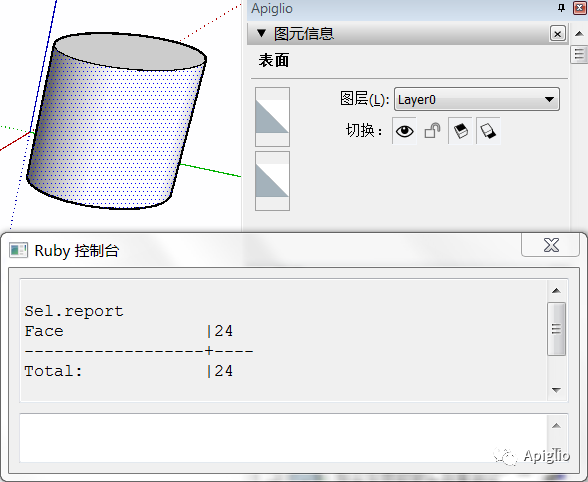
表面图元实际上是多个相连的平面图元的集合,这些平面图元通过软化的边线相连。当点击一个 Face 图元时,如果这个平面能够通过软化边线连接其他平面,那么选择工具就会一并选择符合条件的所有结果。因此点选一个平面时,实际上选区中包含多个平面,图元信息中不显示“N个平面”,而是直接显示“表面”:

如果通过双击选择表面,则会额外选择表面的轮廓;如果是连续三次点击,也就是“选择所有与之相连的图元”,此时就会看到如下的情况:
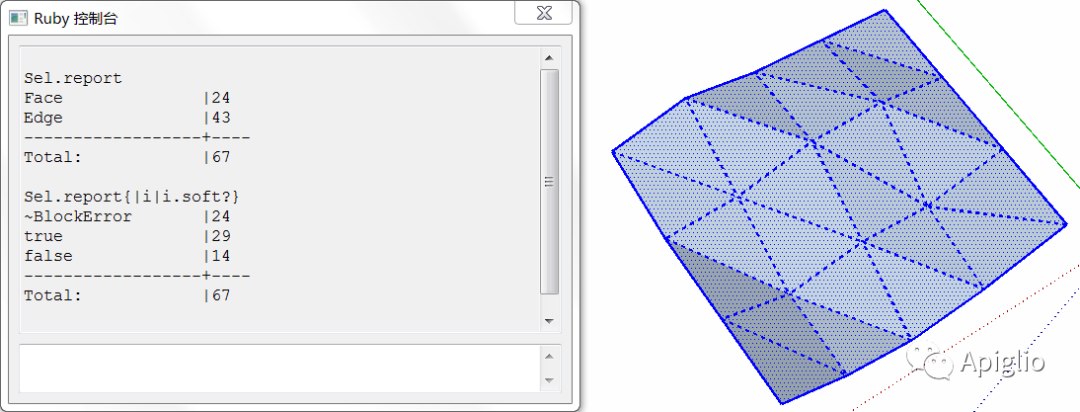
通过选区代码工具 Sel.report 可以得知,此时的选区中有边线和平面两种图元,而边线中又可以分成软化和非软化的两种图元。其中软化的边线就是虚线表示的“隐藏”的边线。
②表面的选择
绘图区自带的选择工具可以在用户点选一个平面图元时选中所有能通过软化边线相连的平面,如果是 ruby 脚本中已知一个平面图元,也可以通过相同逻辑来获得表面所包含的所有平面。这里提供一个实现方法:
module Selmodule Surfdef self.find_surface_by_face(face)surf=[face]len_old=0len=surf.lengthwhile len != len_old dosurf.to_a[len_old..-1].each{|f|f.edges.each{|e|if e.soft? thene.faces.each{|nf|surf<<nf unless surf.include?(nf)}end}}len_old=lenlen=surf.lengthendreturn surfendendend
注:这是选区代码工具 Sel 中新增的一个方法,在已知一个平面图元 f 时,可以通过 Sel<< Sel:: Surf. find_surface_by_face( f) 来选择包含此图元的表面。
③一些特性
由于表面其实是多个平面,因而很多对表面的操作属于批量操作。例如在右键菜单中的“翻转平面”,对于一个表面而言就是依次翻转每一个平面图元:
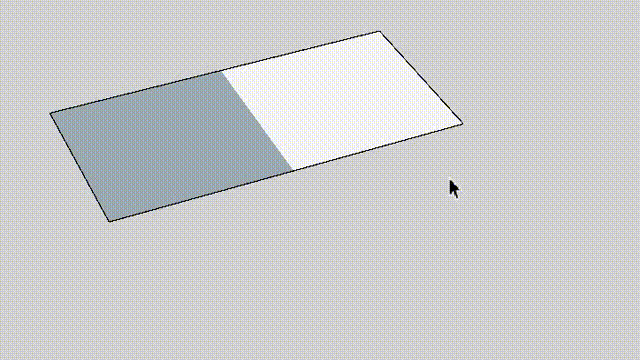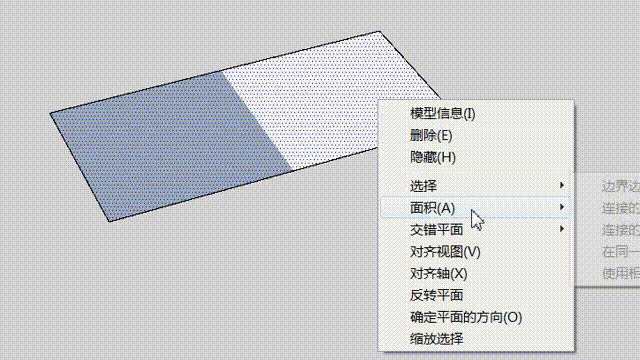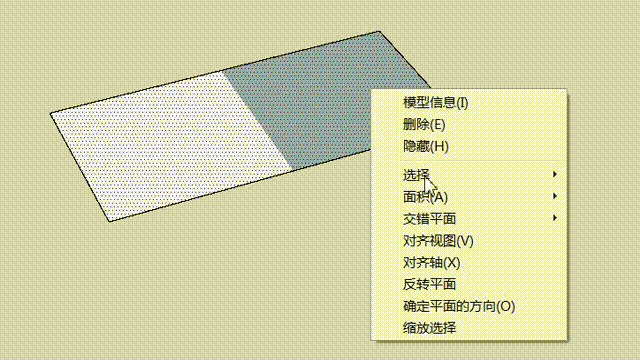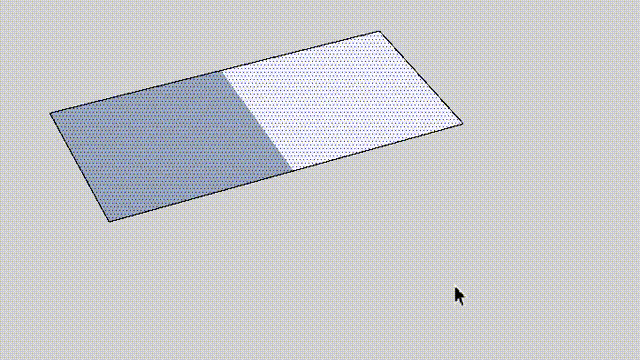
这与 sels. each( &:reverse!) 这样的代码是完全等价的。另外还有专门的统一平面方向的功能,这个相比于翻转平面,功能实现上就稍微复杂,不过原理与上一部分的选择的迭代是差不多的,此处就不举例了。
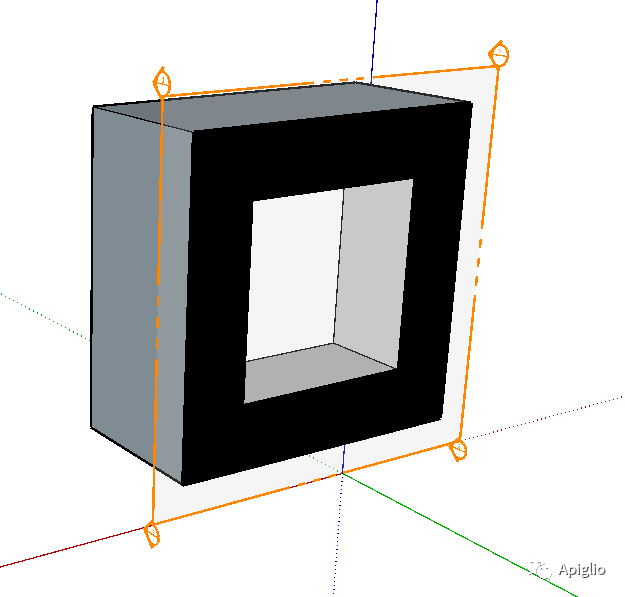
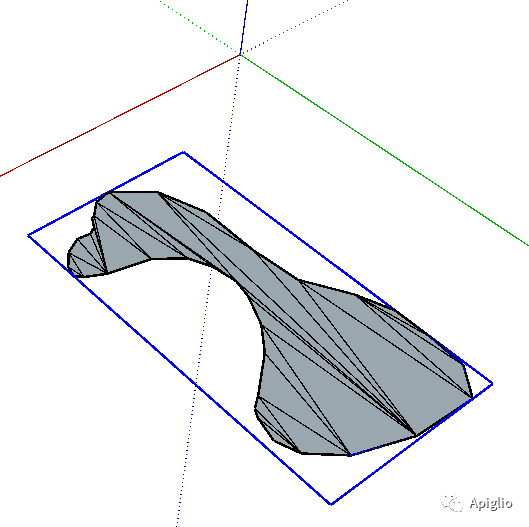
不同于曲线,表面是一个比较宽松的空间概念。因此很多表面图元可以被正确选择,却存在构造上的缺陷。例如以下这种表面:

虽然点选其中一个平面图元可以完整地获取整个表面,但是其中却存在多条未软化的边线,这样不利于表面的呈现,因此可以对这种表面进行修复:
module Selmodule Surfdef self.soft!Sel.sels.grep(Sel::F).each{|f|f.edges.each{|e|if e.faces.all?{|ff|Sel.sels.include?(ff)} and e.faces.length>1 thene.soft=trueend}}.lengthendendend
注:这也是选区代码工具 Sel 中新增的一个方法,用于通过在选中的多个平面中尽可能地创建表面,具体的原理是枚举每一条选中平面连接的边线,如果与边线相连的平面都在选区内,则软化边线。在此处恰好适用于有部分未软化边线表面的修复。
类似于以上方法,可以稍加修改将其改为设置整个表面为平滑光照表面,只需要将 .soft 改成 .smooth 即可。
(2)表面的创建
①软化边线
正如上一部分中修复表面内未软化边线的方法,同样可以使用 Sel:: Surf. soft! 来直接创建表面。这是最便捷的表面创建方法。当然这种方法基于已有的平面和边线,如果是完全新建的图元,则可以根据具体情况自行添加 .soft= true 的指令,完成复杂的表面设计。
不过通常来说这么做意义不大,表面的编辑很有可能使得不同的表面之间端点重合,而造成不必要的粘连,因此还是推荐在每一个表面图元之上套上一个群组或是组件来隔离不同的表面,达到保护表面端点的作用。如果在群组内创建表面,一般而言就不需要具体区分哪一些边线需要软化,就可以使用如下的代码:
grp.definition.entities.grep(Sketchup::Edge).each{|edg|edg.soft=true}
②通过曲线创建
SketchUp 中更为常见的创建表面的方法其实来源于推拉工具和路径跟随。例如绘制一个圆形之后通过推拉,形成的圆柱的侧面就是一个表面:
 |  |
| 圆柱的侧面有24个平面 | 半圆推拉的结果有12个平面 |
另外可以发现,使用默认精度创建的圆与半圆推拉后的侧面同样也符合 24段 / 1圆周 的精度。而半圆推拉后曲面的边缘是曲线端点的推拉结果。因此可以这样理解:
推拉过程中,每一个端点都进行了平移,之后在新的高度上创建一个相同的图形,并且依次连接每一对新旧端点,并依据端点之间的边线创建平面。其中,新创建的边线的 .soft? 属性对标于所对应新旧端点的 .curve_interior? .nil? 的值。
类似于推拉工具,路径跟随也是相似的原理,路径中在曲线内部的点对应产生的平面边线也是软化的,不过在两段路径都是圆弧且端点处切线相同时,路径跟随不会创建非软化的边线,而推拉工具会,这是两者在这一方面的一个微小区别。
③PolygonMesh
——此部分比较难以理解,可选择跳过这一节。
在 Entities 类中有一个 .add_faces_from_mesh 方法,可以通过 Geom 模块中一个很特殊的类型( PolygonMesh 类)来创建表面。Geom 模块中定义的各种类几乎已经在教程的上一个部分“几何与变换”中完全介绍了,此类是少有的例外。这个类型用来创建多面体,主要用来读取和导出其他格式的空间数据文件。这个类的使用场景和具体构造方法会在本篇的第四部分简要介绍,而此处只需要关注段首提到的这个方法。
此方法有四个参数,但只有第一个参数为必要参数。第一个参数需要提供一个 PolygonMesh 类实例,方法会根据此实例创建其所代表的所有边线和平面。第二个参数具体规定边线的显隐、软化和平滑状态,默认的参数为12,意为“全部软化和平滑”。第3、4两个参数分别是创建平面正面和背面的材质,默认为 nil,意为“默认材质”。
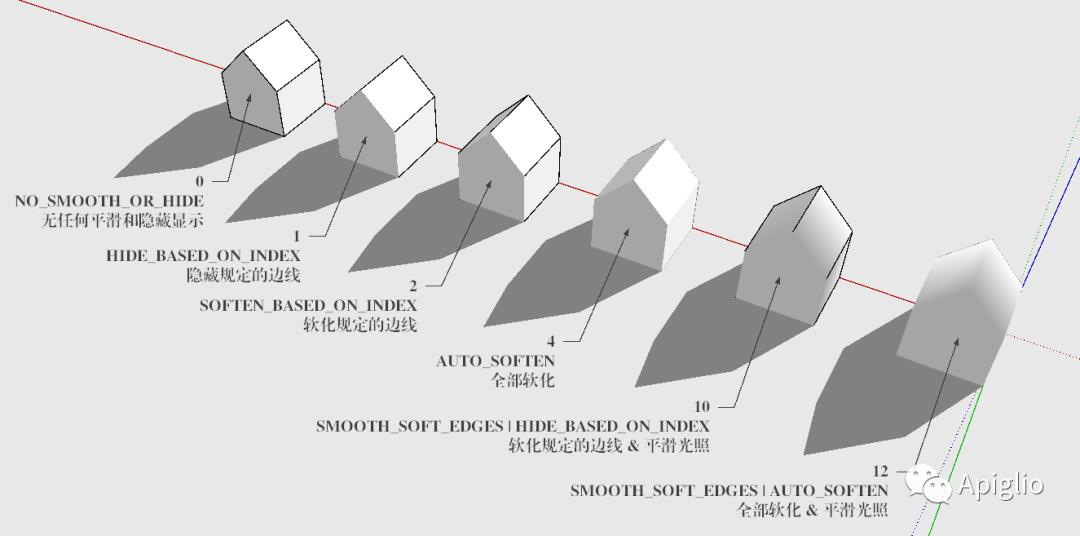
其中第二个参数控制多面体的边线是否软化,因此可以通过此参数来创建多面体表面。这个参数使用二进制位来表示有关设置,共四位。第1位为1时表示“特定”的边线隐藏,第2位为1是表示“特定”的边线软化,第3位为1时表示全部软化(前面两个设置此时无效),第4位为1时软化的边线同时也设置为平滑光照。从SU 2014版本开始,也可以使用常量来表示:
常量名/表达式 | 数值 | 效果 |
NO_SMOOTH_OR_HIDE | 0b0000 | 不隐藏边线 |
HIDE_BASED_ON_INDEX | 0b0001 | 隐藏规定的边线 |
SOFTEN_BASED_ON_INDEX | 0b0010 | 软化规定的边线 |
| 0b0011 | 与0b0010效果相同 | |
AUTO_SOFTEN | 0b0100 | 全部软化 |
SMOOTH_SOFT_EDGES | 0b1000 | 软化的边线平滑光照, 与0b0000效果相同 |
HIDE_BASED_ON_INDEX | SMOOTH_SOFT_EDGES | 0b1001 | 与0b0001效果相同 |
SOFTEN_BASED_ON_INDEX | SMOOTH_SOFT_EDGES | 0b1010 | 软化规定的边线并平滑光照 |
| 0b1011 | 与0b1010效果相同 | |
AUTO_SOFTEN | SMOOTH_SOFT_EDGES | 0b1100 | 全部软化并平滑光照 |
注:以上的常量名定义在 Geom 模块 PolygonMesh 类之中,因此使用时需要额外作出限定,例如常量“ AUTO_SOFTEN ”实际应写成“ Geom:: PolygonMesh:: AUTO_SOFTEN ”。由于这些常数在各个二进制位中是正交的,因此多个常量的组合可以使用“位或”运算,也就是符号 |。
由于软化边线势必会隐藏边线,因此 0b**10 和 0b**11 并没有区别;同样地,当全部软化时,软化规定的边线也被包含在内,因此 0b*100 和 0b*110、 0b*101 也没有区别。
上文中的“规定的边线”是在 PolygonMesh 实例创建过程中进行规定的,详见本篇教程的第四部分。而如果使用 AUTO_SOFTEN 常量, .add_faces_from_mesh 方法创建的图元也就是一个表面图元。
注意,这种方法等同于调用多次 .add_face 方法,不会自动将平面打包成组,因此需要一些额外的工作来确保新图形与原有模型之间没有冲突。
(3)表面的空间计算
表面就是一系列的平面图元,因此储存一个表面图元也只需要使用数组。如果使用选择工具点选了一个表面,那么就可以用以下代码将它储存在数组变量中:
surf=Sketchup.active_model.selection.to_a# 或者在Sel脚本工具中这样使用:surf=Sel.to_a
在遍历“表面”中的每一个图元时,如果不放心可以使用 .grep( Sketchup:: Face) 来进一步筛选平面图元,但是通常这么做是没有必要的,还会无端降低执行效率。
表面常被用在地形建模、规则曲面和不规则形体中,以下就重点以第一种表面为例,提供一些与表面有关的空间计算方法。
①点在表面上的投影
地形建模通常重点关注Z轴方向上的点投影,因此这里提供一个垂直方向的投影到表面的方法以供参考。
def project_point_to_surface(point,surface)plumb_line=[point,[0,0,1]]pi=nilif surface.find{|f|pi=Geom.intersect_line_plane(plumb_line,f.plane)if pi.nil? then falseelsif f.classify_point(pi)==Sketchup::Face::PointOutside then falseelse true end}.nil? thenreturn(nil)elsereturn(pi)endend
此方法需要两个参数,第一个参数 point 表示被投影的点,可以是长度为3的数组或者 Geom:: Point3d 类实例;第二个参数 surface 表示表面,格式必须是只包含平面图元的数组,否则就会报错。方法的返回值是点 point 在表面 surface 上的投影,如果并不存在,则返回 nil。
其原理十分简单,遍历表面中的每一个平面图元,分别过点 point 作一条铅垂线 plumb_line,而后获得其与平面图元所在平面的交点 pi。判断交点 pi 是否在平面图元上,如果符合条件就返回这个交点 pi 的坐标,旋即退出整个计算过程。
这个方法仅限于在Z轴方向上不重复的表面,否则,Z轴上有多个铅垂线交点时,就会返回第一个找到的交点,而忽略其他的。
②表面限制下落
经常需要在地形表面上随机覆盖大量的组件,这时就需要使用这种限制下落方法,以达到所有组件都能正好下落在表面上。直接获取单个组件或群组的底部中心点,然后沿用上一部分的方法计算其在表面上投影,随后根据两点创建变换对象就可以简单地实现这个功能:
def falling_onto_surface(grp,surf)b=grp.boundsbc=b.center-Geom::Vector3d.new([0,0,b.depth])proj=project_point_to_surface(bc,surf)t=Geom::Transformation.new(proj-bc)grp.parent.entities.transform_entities(t,grp)end
使用一个简单的迭代器就能批量调用这个下落方法:
list.each{|g|falling_onto_surface(g,surf)}以下是等距阵列组件在地形表面上的下落效果:


表面限定下落之后通过编辑组件以达到埋入的效果
(4)空间网 Mesh
——此部分设计人员未必接触得到,可选择性地阅读。
①Geom:: PolygonMesh
Geom 模块中定义的类都是与空间关系有关的概念,而 PolygonMesh 也不例外,但是它与之前介绍的点、向量、范围和变换等概念相比,更加复杂——是一系列点与其所组成的表面。它和“表面图元”的关系就像 Geom:: Point3d 和 Sketchup:: Vertex 的关系一样:前者是空间概念,可以脱离模型存在,不单独保存在模型存档中;后者是模型中明确的部件,能够保存在文档之中。
前文已经介绍过 Entities 类中的 .add_faces_from_mesh 方法,其中的第一个参数便需要此类型的实例。尝试以下代码:
mesh = Geom::PolygonMesh.newoa=100ob=200ia=120ib=180mesh.add_point(Geom::Point3d.new(oa,oa,oa))mesh.add_point(Geom::Point3d.new(oa,oa,ob))mesh.add_point(Geom::Point3d.new(oa,ob,ob))mesh.add_point(Geom::Point3d.new(oa,ob,oa))mesh.add_point(Geom::Point3d.new(ob,oa,oa))mesh.add_point(Geom::Point3d.new(ob,oa,ob))mesh.add_point(Geom::Point3d.new(ob,ob,ob))mesh.add_point(Geom::Point3d.new(ob,ob,oa))mesh.add_point(Geom::Point3d.new(ia,ia,ia))mesh.add_point(Geom::Point3d.new(ia,ia,ib))mesh.add_point(Geom::Point3d.new(ia,ib,ib))mesh.add_point(Geom::Point3d.new(ia,ib,ia))mesh.add_point(Geom::Point3d.new(ib,ia,ia))mesh.add_point(Geom::Point3d.new(ib,ia,ib))mesh.add_point(Geom::Point3d.new(ib,ib,ib))mesh.add_point(Geom::Point3d.new(ib,ib,ia))mesh.add_polygon(4,3,2,1)mesh.add_polygon(5,6,7,8)mesh.add_polygon(1,2,6,5)mesh.add_polygon(2,3,7,6)mesh.add_polygon(3,4,8,7)mesh.add_polygon(1,5,8,4)mesh.add_polygon(12,11,10,9)mesh.add_polygon(13,14,15,16)mesh.add_polygon(9,10,14,13)mesh.add_polygon(10,11,15,14)mesh.add_polygon(11,12,16,15)mesh.add_polygon(9,13,16,12)ents=Sketchup.active_model.entitiesents.add_faces_from_mesh(mesh,Geom::PolygonMesh::NO_SMOOTH_OR_HIDE)
以上代码,首先创建了一个新的实例,之后在实例中依次添加了16个顶点,再根据顶点序号创建12个平面。最终通过 .add_faces_from_mesh 方法将其绘制在当前模型中:
|
|
| 创建结果 | 剖切后的效果 |
使用 PolygonMesh 创建平面相当于将一次性创建所有它所包含的平面,对于上述的例子,也可以完全替换为 .add_face 方法的版本。不过,在已知点位的情况下,绘制简单的立体图形其实并不需要使用 PolygonMesh,它更适合用与复杂的立体图形,更重要的是它支持调整不同平面之间的材质坐标(UV坐标),不过材质的内容会在下一个大部分“图元属性”中再进行介绍,此处不会涉及。
此处关注一下 PolygonMesh 类的实例方法,包括以下三大类:(1)编辑顶点或平面;(2)查找顶点或平面点集;(3)材质坐标。
编辑的方法包括之前例子中使用的 .add_point 和 .add_polygon 方法:前者根据 Point3d 创建顶点,并且返回创建的顶点在 Mesh 中的编号;后者使用这些编号定位点坐标,创建 Mesh 中的各个平面,至少需要三个顶点编号,也支持更多共面的点。这里需要注意,不同于通常情况下数组的下标,这里顶点编号是从 1 开始的,编号 0 则作为异常值的返回结果。由于端点编号为非负整数,因此在 .add_polygon 方法的参数中如果使用负数编号则表示此平面为隐藏边线的平面,对应上文中的“规定的边线”。 .add_point 方法后跟两个参数,第一个参数为端点编号,第二个参数为 Point3d 类用于修改特定编号端点的位置。 .transform! 方法与其他空间类概念相同,后跟变换类参数,用于变换整个空间网。
查找顶点的方法包括统计方法和具体的查找引用方法。 .count_points 和 .count_polygons 方法分别返回 Mesh 中定义了几个顶点和几个平面。 .normal_at 方法返回具体编号顶点所在处的法线,返回的是 Vector3d 类。 .point_at 方法返回具体编号端点的位置; .points 方法依编号顺序返回所有的端点的坐标。需要特别指出, .points[0] 相当于 .point_at(1),两者编号有1位的偏移。 .polygon_at 和 .polygons 方法与前两个方法类似,不过返回的是组成平面的点编号数组,编号顺序决定平面的朝向。 .polygon_points_at 方法在 .polygon_at 的基础上返回每一个点的具体位置 。 .point_index 方法则根据具体位置查找对应顶点的编号,未找到则返回 0。
以下两组代码组内返回结果均相同:
# 返回顶点集mesh.points(1..mesh.count_points).map{|indx|mesh.point_at(indx)}# 返回编号为2的平面每一个点的空间位置mesh.polygon_points_at(2)mesh.polygon_at(2).map{|v|mesh.point_at(v)}mesh.polygons[1].map{|v|mesh.point_at(v)}mesh.polygons[1].map{|v|mesh.points[v-1]}
另外还有 .set_uv、 .uv_at 和 .uvs 三个方法,涉及材质坐标,此处不展开。
②Mesh 的获取方式
空间网有两个获取来源,一个是通过 PolygonMesh 类的构造方法创建,即前文使用的 .new 方法;另一种则是通过 Face 类的 .mesh 方法获得。
第一种方法会创建空白的 Mesh 对象,有两个可省略的参数,依次为端点数量和平面数量,这些参数并不会改变初始 Mesh 对象的定义,只会影响创建对象时预先加载的内存大小。
第二种方法是基于模型中已有的平面图元而创建的,并且创建的 Mesh 所有平面均为三角形,这对于移动不规则平面中的个别顶点非常有意义。
#打开组件内的平面,只选择一个平面图元f=Sel.sels[0]#用f表示群组内选中的平面ents=Sketchup.active_model.entitiesmtemp=f.mesh#按照相对坐标绘制:ents.add_faces_from_mesh(mtemp,0)#转换为绝对坐标绘制:mtemp.transform!(Sel.sels[0].transformation)ents.add_faces_from_mesh(mtemp,0)
执行以上代码可以发现,此方法为已存在的平面创建了一个特殊的 Mesh 结构,全部由三角形组成。需要注意,如果是群组或组件内的平面,其坐标是相对于组件定义而言的,所以如果是组件内的平面以此法在主模型中创建空间网,就会不会和原平面重叠。
|  |
相对坐标 | 根据群组属性偏移后的坐标 |
另外, .mesh 方法之后有一个可省略的参数,其数值含义也与二进制位有关。当第1位为 1 时返回结果包含正面材质坐标信息,当第2位为 1 时包含背面材质坐标信息,当第3位为 1 时包含法线信息。此参数默认值为 0,表示返回的 Mesh 只储存点位置信息。
三角网的好处在于,每一个顶点都没有共面限制,可以任意移动位置,因此可以利用这一点,对已存在的平面进行变形,将其转换成表面图元。以下是一个示例:
def liftVertex(verx,face,height)raise ArgumentError("Param1 Must Be A Vertex.") unless verx.is_a?(Sketchup::Vertex)raise ArgumentError("Param2 Must Be A Face.") unless face.is_a?(Sketchup::Face)raise ArgumentError("Param3 Must Be Length or Any Other Numeric Data") unless height.respond_to?(:mm)raise ArgumentError("Vertex Must Be One of Face Vertices.") unless face.vertices.include?(verx)mesh=face.mesh#这里我只考虑了外环的情况circum=face.loops[0].edges.map(&:length).inject{|i,j|i+=j}vs=face.loops[0].vertices.to_av=vs.index(verx)cnt=vs.lengthls=[]for i in 0..cnt-1 doif i==v thenls<<0elselen=0toi= i>v ? v+cnt : vfor tmp in i..toi dolen+=face.loops[0].edges[tmp%cnt-1].lengthendif len>circum/2 then len=circum-len endls << lenendendls.each_with_index{|len,indx|ptr_index=mesh.point_index(vs[indx].position)posi=mesh.point_at(ptr_index)posi.transform!(Geom::Transformation.new([0,0,height*len/circum*2]))mesh.set_point(ptr_index,posi)}return meshend
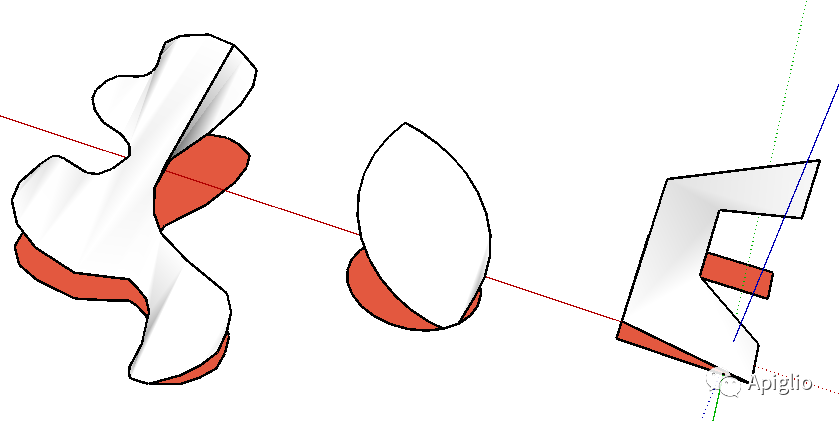
此方法可以在给定一个平面、一个顶点和一个初始抬升高度的前提下,对平面进行沿周长方向递减的抬升变形。可以在控制台输入如下代码:
# sels,ents 定义如常face=sels[0]verx=sels[0].start# 将face和verx分别指向已存在的图元mesh=liftVertex(verx,face,1000)ents.add_faces_from_mesh(mesh,12)# 12: Geom::PolygonMesh::AUTO_SOFTEN | Geom::PolygonMesh::SMOOTH_SOFT_EDGES
具体的效果如下:
③Mesh 的用途
空间网的使用场景并不是非常广泛,官方给出的用途解释是与 Sketchup:: Importer 一起使用,作为读取其他格式文件的便捷工具,尤其是大部分三维模型文件都采取类似的逻辑构建,因此在编写转化器时逻辑上会比较方便。
例如以下是一个简单模型的 obj 文件(左),它是使用 Ruby 脚本通过 PolygonMesh 创建的(右),将此模型转出成 obj 文件并与原代码进行对比,可以发现基本完全能够对应:
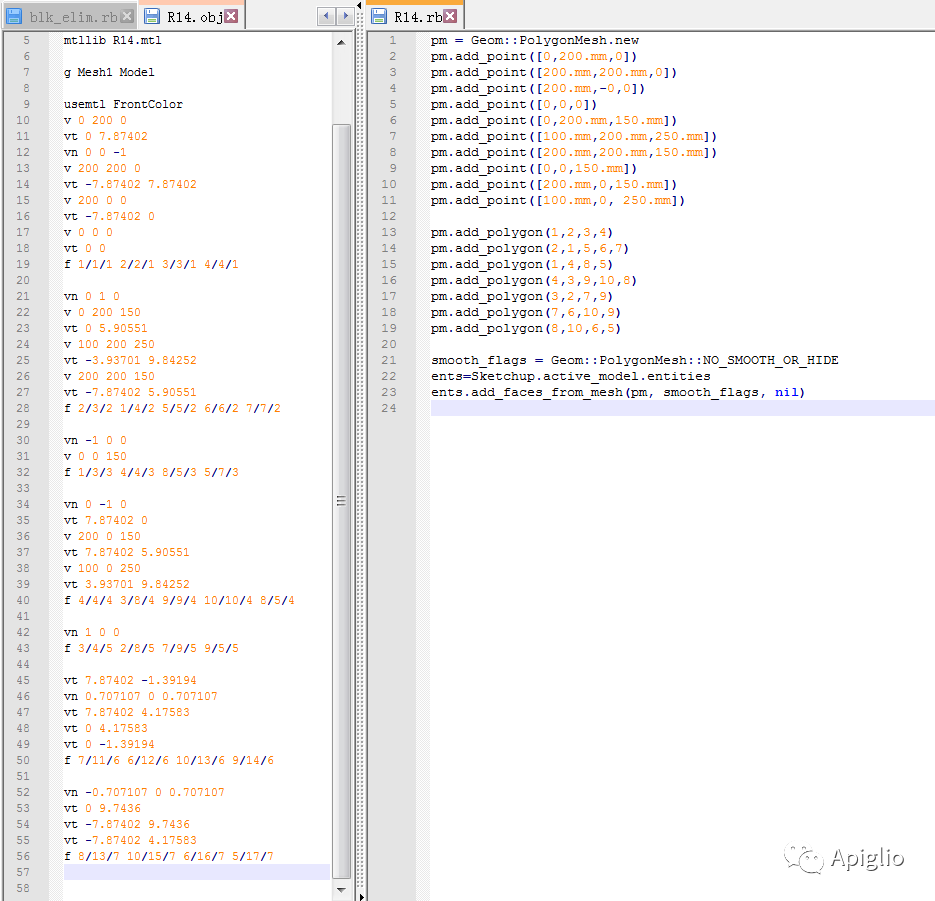
左侧 obj 格式中的 v 即定义点坐标,对应右侧 ruby 的 .add_point;vt 是材质坐标(UV坐标),vn 为法线数据;f 则定义一个平面,对应 .add_polygon。空间网有点坐标和平面点集就可以创建图形,而法线和材质信息是由 SketchUp 的默认设置确定的。而如果要导出为 obj 格式,文件格式需要这些数据,在使用平面图元的 .mesh 方法时,其后的参数就必须要包括法线和正反面UV坐标,也就是 7。
本篇教程原计划是,简要介绍表面这种“定义上地位尴尬又十分重要”的概念性图元。考虑到篇幅较短,就决定把之前 Geom 模块剩余的一个类 PolygonMesh 类一并介绍了。这两个概念确实有很多相通之处,并且后者也可以用于创建各类表面,因此还算是比较巧合。其中的一些功能的代码实现示例可能比较潦草,可读性和功能稳定性都或有缺憾,不过教程中的例子还是以启发为主。
下一篇就进入最为缤纷绚丽的群组和组件了,这一部分教程之前在一些小灵感的作品中不断地有出现,可以先观看这些篇目:
(完)
本文编号:SU-R14