【SU Ruby教程】图元定义(4):曲线类

在 SketchUp 中,有两类图元非常特殊,表现为多个图元的组合,即曲线和表面。这两类图元的特点是可以一次点击选择整个图元,而实际上是选择了从属于此图元的所有具体图元。这种图元被称为概念性图元( conceptual entity )。
本篇教程介绍曲线图元,表面图元则放在下一篇。在这两篇教程中,会提前使用到选区的概念,用于测试示例代码,因此有必要再提一下 SketchUp 选区的基本使用方法:
sels = Sketchup.active_model.selection之后的篇幅中 sels 就表示当前模型的选区。选区类根据用户界面中的实时状态,返回所有被选中的图元,因此也是图元类的容器类,其使用方法可以参照 Entities 类。
另外,示例中有可能出现诸如以下的代码:
Sel<<[ent]其中的 Sel 为本人的自定义模块,以上代码表示将 ent 图元纳入选区。等价于如下不使用此模块的表达:
Sketchup.active_model.selection.add(ent)#或sels.add(ent)
也可以直接参考此篇文章 [SU-2021-05],下载和使用此模块。
图元定义(4):曲线类
| 【本期目录】 | |
| (1)SU曲线的特性 ①曲线的本质 ②曲线的选择 ③曲线的种类 | (3)编辑曲线 ①曲线的打断 ②曲线的续接 ③曲线成面 ④自由变换 |
(2)曲线的创建 ①一般的绘制方法 ②圆形与多边形 ③圆弧 ④焊接 | |
(1)SU 曲线的特性
①曲线的本质
SketchUp 中并没有真正意义的曲线,而是由一组首尾依次相连的边线图元组成的多段线。在绘制和点选曲线时,SketchUp 能够区分哪一些边线属于哪一个曲线,这是因为每一个边线图元都会记录自己所属的曲线;与上一篇中的 EdgeUse 类和边线类的关系相似,代表曲线概念的 Curve 类也是以这种引用的形式来联系曲线概念与实际的边线图元的。
正如以下例子中,模型中仅有一条曲线,但是图元容器中却显示有多个边线图元:
#令当前模型仅包括一条曲线ents=Sketchup.active_model.entitiesputs ents.count#>> 12puts ents.all?{|e|e.is_a? Sketchup::Edge}#>> true
通过这些边线图元的 .curve 方法就可以得到这条曲线的概念性图元:
p ents[0].curve#>> #<Sketchup::ArcCurve:0x0000000bec5e68>p ents[0].curve.is_a? Sketchup::Curve#>> true
ArcCurve 是 Curve 的一个子类,所以本例中虽然显示这个曲线是 ArcCurve 但是它同样满足是 Curve 类的要求,也同时继承有 Curve 的所有方法。
曲线类 Curve 的实例方法中,首先是与边线图元建立关系的方法,包括 .edges、 .first_edge、 .last_edge、 .each_edges 和 .count_edges 这几个方法。其中 .edges 方法返回构成这一条曲线的所有边线图元,依次保存在一个数组中。其余方法可以理解成 .edges[0]、 .edges[-1]、 .edges. each 和 .edges. count 等表述。
类似的还有 .vertices 方法,返回的是端点的数组。对于端点而言,有一个 .curve_interior? 方法用于判断端点是否是曲线内部的一个点:
verts=ents.map(&:vertices).flatten.uniqverts.all?{|i|i.is_a?(Sketchup::Vertex)}#>> trueverts.map{|i|i.curve_interior?}#>> [nil, #<Sketchup::ArcCurve:0x0000000bec5e68>,#>> #<Sketchup::ArcCurve:0x0000000bec5e68>, #<Sketchup::ArcCurve:0x0000000bec5e68>,#>> #<Sketchup::ArcCurve:0x0000000bec5e68>, #<Sketchup::ArcCurve:0x0000000bec5e68>,#>> #<Sketchup::ArcCurve:0x0000000bec5e68>, #<Sketchup::ArcCurve:0x0000000bec5e68>,#>> #<Sketchup::ArcCurve:0x0000000bec5e68>, #<Sketchup::ArcCurve:0x0000000bec5e68>,#>> #<Sketchup::ArcCurve:0x0000000bec5e68>, #<Sketchup::ArcCurve:0x0000000bec5e68>,#>> nil]
这个方法以问号结尾,但是并非返回真假,而是返回具体的曲线类或者 nil,当然,对于 ruby 来说,这样的结果同样可以用在 if 语句,这也是这个方法带有问号结尾的原因:
if verts[2].curve_interior? thenputs "Vertex is interior."elseputs "Vertex is NOT interior."end
除了以上与边线类、与端点的关系以外,Curve 类还提供 .length 方法,返回这段曲线的长度,可以理解成以下的表达:
curve.edges.map(&:length).inject{|sum,i|sum+=i}如果使用上述例子中绘制的圆弧来进行测试,以上代码的结果与 curve. length 的结果存在区别,这是因为 ArcCurve 类的 .length 方法不同于此,有单独的方法覆盖父类 Curve 的同名方法。
②曲线的选择
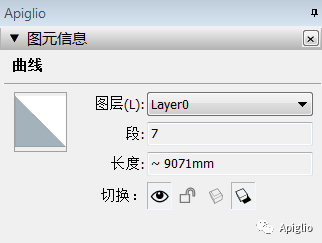
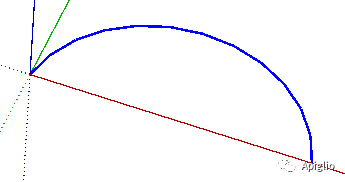
了解了曲线的定义以后,再回来看绘图区域中曲线的特点可以发现,Sketchup 的图元信息窗口显示的图元名称会根据曲线的具体类型不同而呈现不同名称:
| 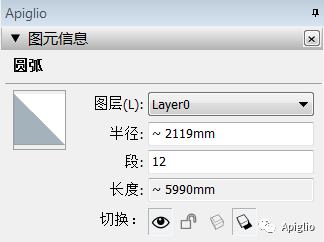 |
|
|
|
|
但是如果同时选择两条或以上的曲线,它就会改为显示“N条边线”:
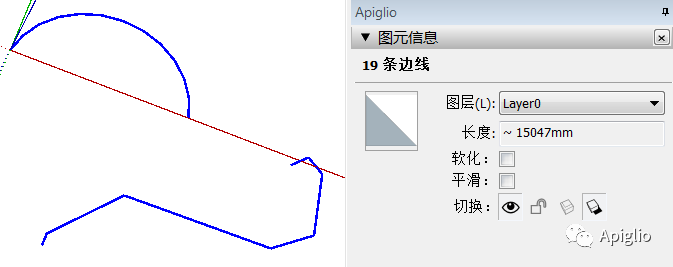
如果在仅选取一条曲线后用代码取消选择其中一段边线,也同样会改为显示“N条边线”,无论这条边线是否在曲线的尽端:
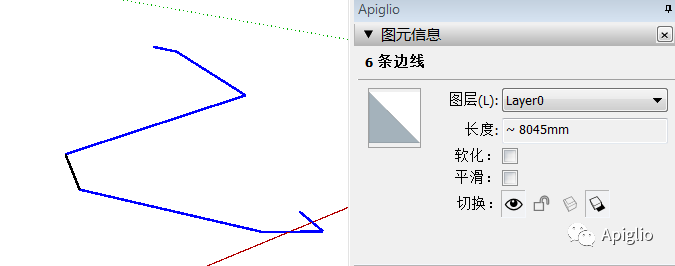
所以我们可以通过代码来模拟图元信息窗口的这一显示原理:
def showSelectionEntsdOut=proc{|size|puts(size.to_s+(size>1 ? " edges" : " edge"))}#定义了一个默认的输出格式,返回“N edge(s)”sels=Sketchup.active_model.selectionunless sels.all?{|e|e.is_a? Sketchup::Edge} then raise ArgumentError.new("Only select Edges!") end#如果选区中包含边线以外的图元则报错,这不在这个测试方法的适用范围内curves=sels.map(&:curve).uniqif curves.length!=1 thendOut.call(sels.length) # curve结果不唯一时表示有不同的曲线elseif curves[0].nil? thendOut.call(sels.length) # curve结果均为nil表示没有曲线elseif curves[0].edges.all?{|e|sels.include?(e)} thenif curves[0].is_a?(Sketchup::ArcCurve) thenputs "ArcCurve" # 这里输出“圆弧”,但是具体是什么圆弧这里不进一步描述elseputs "Curve" # 这里输出“曲线”endelsedOut.call(sels.length) # curve的部分边线不在选区内endendendend
当我们选择一个曲线时,SU 实际接收到的是我们点击了一个边线图元,而它需要把边线图元所在的曲线所含的所有边线一并加入选区,类似于以下过程:
# 通过鼠标点击工具获得一个图元 chosen_edge# chosen_edge=view.pick_helper.best_picked # PickHelper的内容会在比较后面介绍if chosen_edge.is_a? Sketchup::Edge thenedges_in_the_same_curve=chosen_edge.curve.edgessels.add(edges_in_the_same_curve) # 追加选择#sels.remove(edges_in_the_same_curve) # 移除选择#sels.toggle(edges_in_the_same_curve) # 切换选择状态end
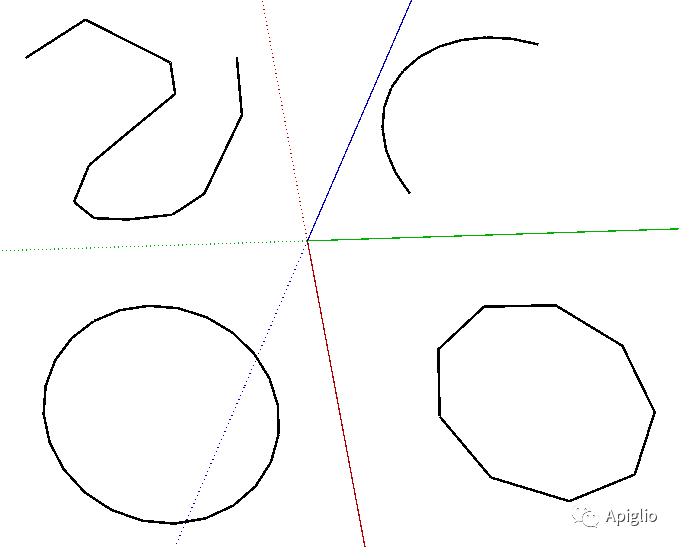
③曲线的种类
在上一部分中我们已经了解了图元信息窗口会根据图元的不同,显示不同的图元名称,例如“曲线”和“圆弧”。这就是两种不同的曲线。SketchUp 中的曲线包含以下几种:
(i) 曲线
这是最普遍的一类,没有任何的额外规定,任何一组首尾相连的边线都可以组成这样的曲线。这种曲线的概念性图元类是 Curve 类实例。
(ii)圆弧
这是一类特殊的曲线,它的创建需要符合一定的规则,需要确定中心点、半径和所在平面等属性,是有一系列限制的曲线。这种曲线的概念性图元类是 ArcCurve 类实例。相比于前者,有一些单独的特性。
(iii)圆
圆弧的特例,如果一个圆弧首尾相连,它就是圆。圆弧和圆可以相互转换,有单独的创建方法。但是需要特别注意,它本质上是正多边形。
(iv)多边形
圆弧的另一个特例,圆的孪生概念,基本上和圆没有任何区别,只是它被叫作“多边形”而已。它们的区别只是创建时的申明不同。
(2)曲线的创建
①一般的绘制方法
曲线的一般创建方法是 Entities 类的 .add_curve 方法,这个方法的参数使用情况完全与 .add_edges 方法相同,只是创建的图元结果不同。
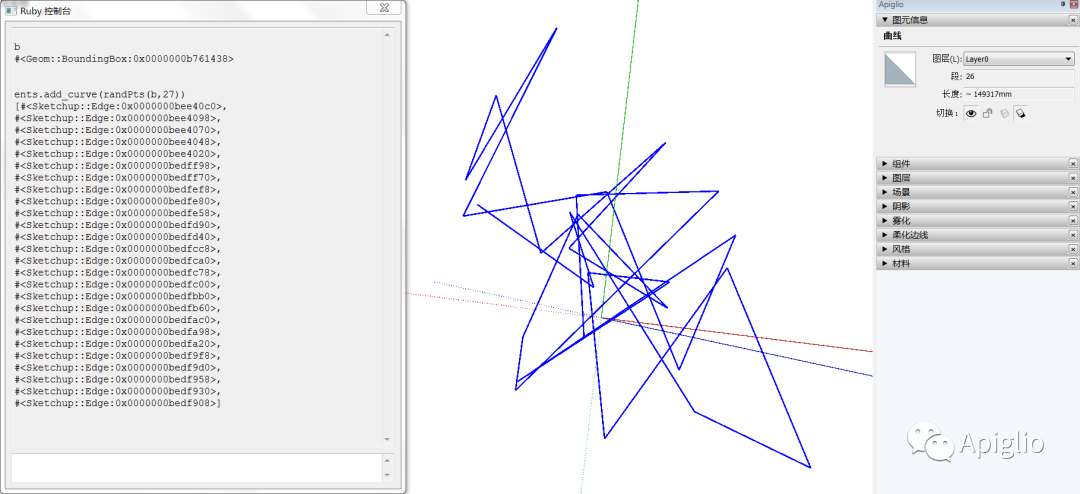
上图中直接随机生成了27个点坐标,并以此绘制曲线。需注意此方法返回的是新创建的所有边线组成的数组,而非 Curve 类实例,这一点与“add_curve”这个名字有些许冲突,和 .add_edges 方法保持一致。因此如果需要在创建后取得曲线的引用则需要使用如下的代码:
edges=ents.add_curve(randPts(b,27))curve=edges[0].curve unless edges[0].nil?
②圆形与多边形
圆形和正多边形的绘制相比于普遍的曲线,更加规范。它们的创建需要使用 Entities 类的 .add_circle 和 .add_ngon 方法。两个方法都有四个参数:第一个参数确定图形的中心坐标,第二个参数确定图形所在平面法向量,第三个参数确定图形的半径,第四个参数确定图形的边线数量。
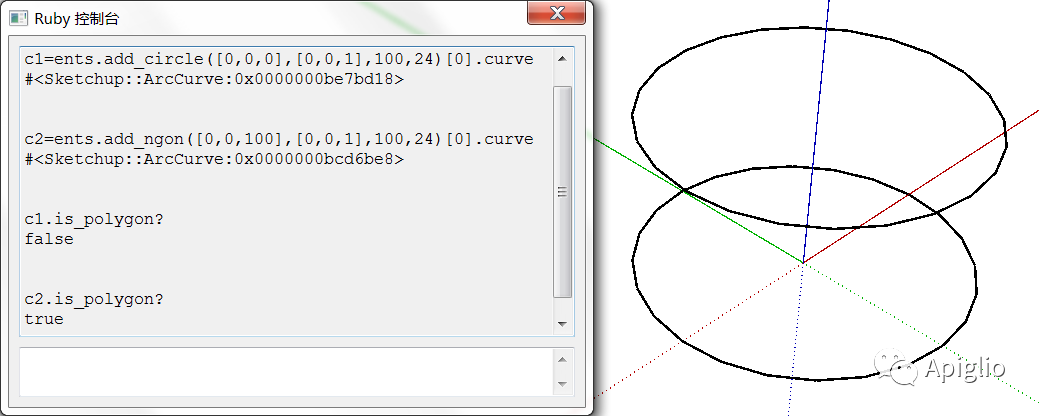
上图可以看到使用 .add_circle 和 .add_ngon 方法在参数相同的情况下,创建的曲线图形外观上完全相同。唯一的区别在于使用 Curve 类的 .is_polygon? 方法检验时,两者会返回相反的结果。这也是图元信息窗口判断哪些曲线是圆哪些是多边形的方式。可以说这两个方法的绘图部分是相同的,只是 .add_ngon 方法绘制后将图元的一个布尔属性设置成了 true,仅此而已。
另外在绘制多边形时,第四个参数就表示边线数量;而绘制圆时,这个参数表示的则是绘图精度。作为绘图精度,这个参数拥有默认值24,这也就是说 .add_circle 方法可以只接受三个参数,这是两个方法之间的另外一个小区别。
绘制圆形和多边形时,创建的是 ArcCurve 类实例,因此它还会额外储存一些别的信息。创建图元时的前三个参数都会保存在这个圆弧类的属性中,可以使用 ArcCurve 类的 .center、 .normal 和 .radius 方法来访问。另外可以用 .plane 方法获得其所在的平面,当然这个值完全可以通过 .center 和 .normal 计算出来。
正是由于有这些额外的参数, ArcCurve 类的 .length 方法也根据这些参数计算,而不会对各个边线长度进行求和。
③圆弧
圆弧是打断的圆,可以理解成是圆的一个部分,因此圆弧的绘制可以参考圆的绘制。绘制圆需要 Entities 类中的 .add_arc 方法,有7个参数,依次为中心、起始方向、旋转法向量、半径、起始角度、结束角度和段数。其中最后一个参数表示精度,可省略。
以下创建三个不同方向上的圆弧:
c1=ents.add_arc([0,0,0],[1,0,0],[0,0,1],10,0.degrees,270.degrees)[0].curvec2=ents.add_arc([0,0,0],[1,0,0],[0,1,0],12,0.degrees,270.degrees)[0].curvec3=ents.add_arc([0,0,0],[1,0,0],[0,1,1],14,0.degrees,270.degrees)[0].curve
代码运行结果如下:
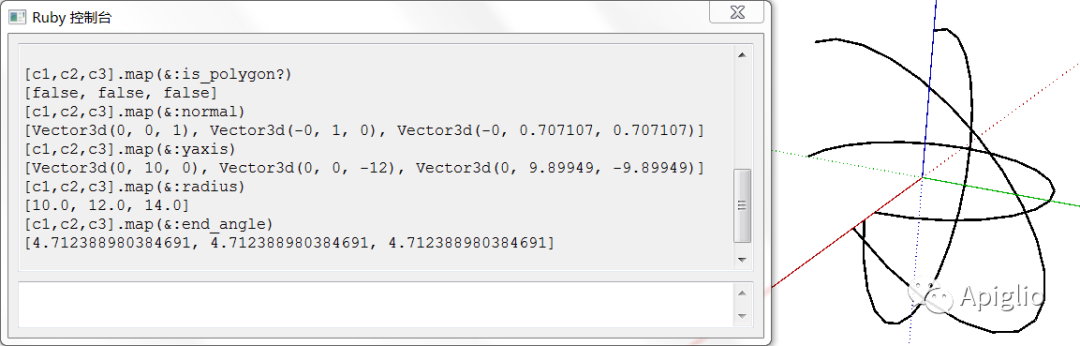
得到的 ArcCurve 实例可以使用 .start_angle、 .end_angle 和 .xaxis 方法得知上述方法中创建时的参数,也可以通过 .yaxis 方法得到垂直于起始角度和旋转轴的第三轴。
.yaxis 方法的结果的方向与起始角度(xaxis)和旋转轴的积结果相同:
[c1,c2,c3].map{|c|(c.normal*c.xaxis).samedirection?(c.yaxis)}#>> [true, true, true]
如果给定的参数中起始方向与旋转轴不是正交的,那么 SU 会优先使用起始方向,然后据此重新计算一个正交的旋转轴。这样可以确保圆弧的起始点在 center + xaxis 处。
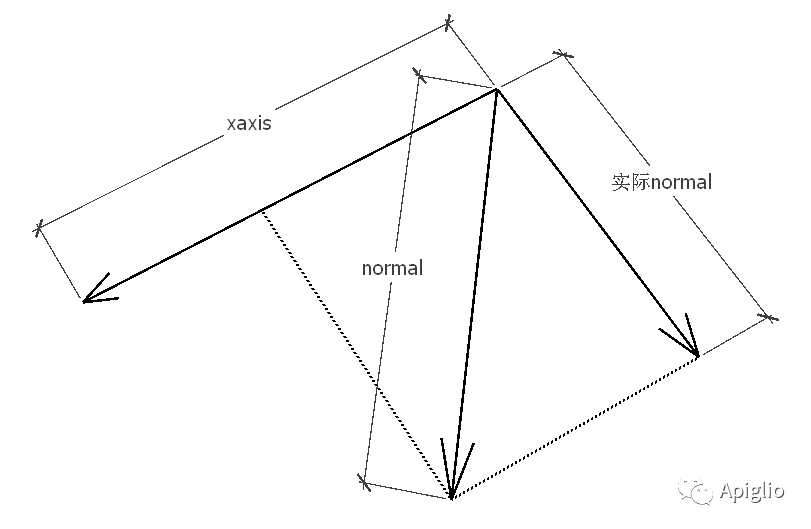
当然,一般还是尽量避免使用这种自动更正的特性。
另外,最后一个参数同样是表示绘制精度,默认的精度是“24段/1圆周”,这意味着创建圆弧的默认段数是圆心角百分度(Grad)与24的乘积,可以使用如下代码自行验证:
curves=[]for i in 1..360 docurves<<ents.add_arc([0,0,i],[1,0,0],[0,0,1],10,0.degrees,i.degrees)[0].curveendcurves.each{|c|puts "angle= #{c.end_angle.radians.round}\tseg= #{c.count_edges}"};nil
以缺省参数连续创建多个不同圆心角的圆弧,并输出它们的段数,可以得到以下结果:
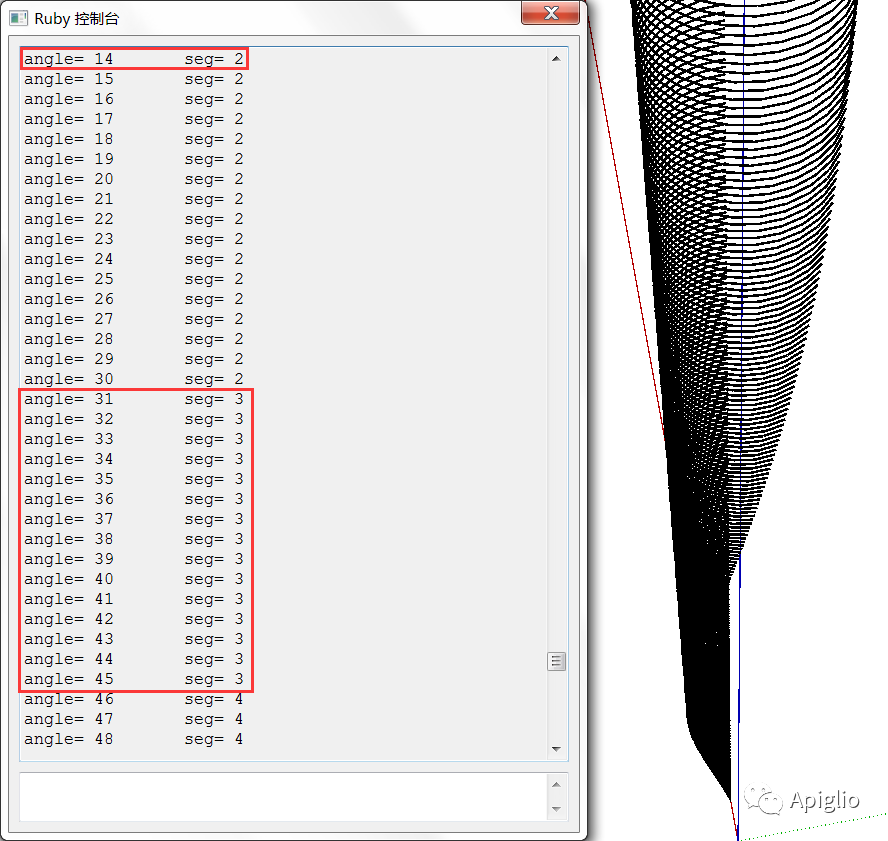
可以发现,当圆心角每增加15°,边线段数增加1,唯一的特例是圆心角小于15°的圆弧也会保证有2段边线。
以上是 Entities 类的 .add_arc 方法,它的绘制过程相当于绘制工具中默认的圆弧工具,可以称之为“圆心式”。但是这种绘制方式并不够强大,所以 SU 在绘图工具中提供了另外两种绘制方式“两点圆弧”和“三点圆弧”,能够适应更多的绘图任务。
但是这两种方式并不直接出现在 ruby API 之中,这就需要自己创建自定义方法了。在这里我补充两段代码用于实现“两点圆弧”和“三点圆弧”。
补充方法①:三点圆弧
def add_arc_3point(*arg)if arg.length==3 then pts=arg.to_a elseif arg[0].is_a? Array then pts=arg[0].to_aelse raise ArgumentError.new("3 Point3 Required.") endendpos=pts.map{|p|Geom::Point3d.new(p)}v1=pos[0]-pos[1];v2=pos[2]-pos[1]v1.length=v1.length/2v2.length=v2.length/2m1=pos[1]+v1;m2=pos[1]+v2plane=Geom.fit_plane_to_points(pos)normal=Geom.intersect_plane_plane([m1,v1],[m2,v2])center=Geom.intersect_line_plane(normal,plane)radius=center.distance(pos[0])vector_0=pos[0]-centervector_1=pos[1]-centervector_2=pos[2]-centerang01=vector_0.angle_between(vector_1)ang02=vector_0.angle_between(vector_2)ang12=vector_1.angle_between(vector_2)if (ang02-(ang01+ang12)).abs<0.000001 thenunless normal[1].samedirection?(vector_1*vector_2) then normal[1].reverse! endea=ang02elseea=2*Math::PI-ang02if (ang01-(ang12+ang02)).abs<0.000001 thenunless normal[1].samedirection?(vector_1*vector_2) then normal[1].reverse! endelseunless normal[1].samedirection?(vector_0*vector_1) then normal[1].reverse! endendendSketchup.active_model.entities.add_arc(center,vector_0,normal[1],radius,0,ea)return nilend
补充方法②:两点圆弧
def add_arc_2point(pt1,pt2,vec)unless pt1.respond_to?(:on_line?) then raise ArgumentError.new("Point3d or Array required.") endunless pt2.respond_to?(:on_line?) then raise ArgumentError.new("Point3d or Array required.") endunless vec.respond_to?(:normalize) then raise ArgumentError.new("Vector3d or Array required.") endpos1=Geom::Point3d.new(pt1)pos2=Geom::Point3d.new(pt2)vector=Geom::Vector3d.new(vec)chord=pos2-pos1mid_chord=chordmid_chord.length=chord.length/2mid=pos1+mid_chordnormal_vector=chord*vectordepth_vector=normal_vector*chorddepth_vector.length=depth_vector.dot(vector)/depth_vector.lengthpos3=mid+depth_vector#两点弧就偷懒用三点的方法好了,大概这个意思add_arc_3point(pos1,pos3,pos2)end
以上两种方法的圆弧精度都采用默认设置,如果需要增加精度参数,需要额外的参数定义和类型判断,这里限于篇幅就不加入精度参数了。
④焊接
除了 Entities 类的 .add_* 方法,从 SU2020.1 开始, Entities 类还提供一个新的方法 .weld 来创建曲线——通过已有的边线组合成新的曲线。
注:下文中有关此方法的测试是在 SU2021.1 版本中进行的,而不同于其他部分。未说明版本时,教程中的例子均是在 SU2018 中测试通过。
sels=Sketchup.active_model.selectionents=Sketchup.active_model.entitiesents.weld(sels.grep(Sketchup::Edge))
如果选区中的边线能够构成一个曲线,就焊接成一条曲线,如果存在多条,此方法会自行识别,而后分别焊接:
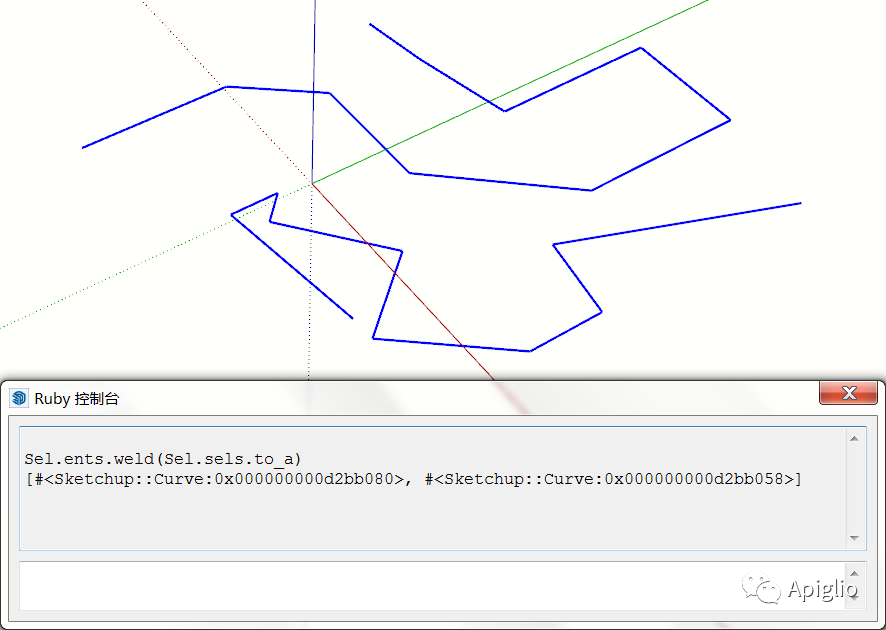
同时还可以检测分叉:
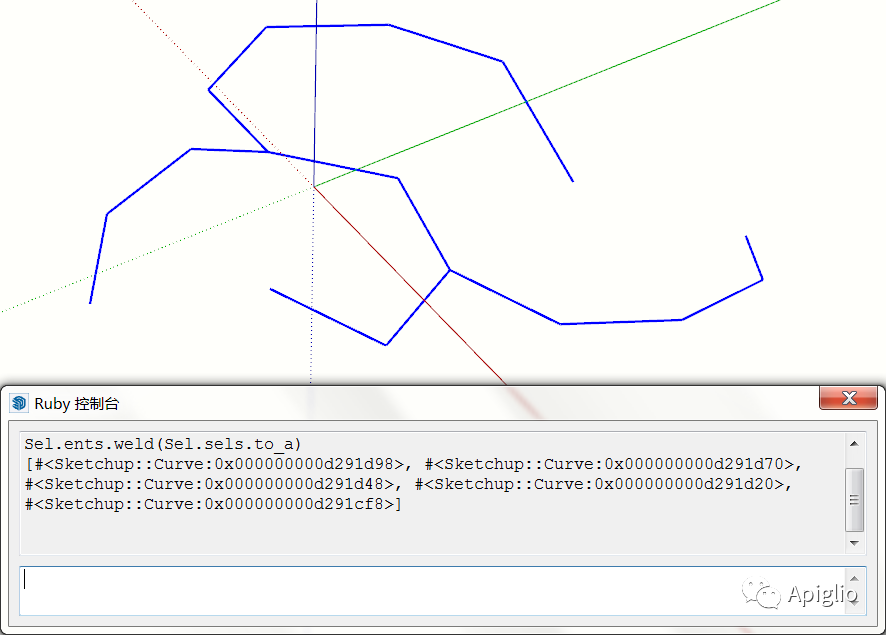
返回值为一个数组,通常情况不会出现空数组的返回结果,因为即使是一条边线,也存在单边线的曲线结构。
(3)编辑曲线
①曲线的打断
曲线的打断可以分为两种,一个是炸开整段曲线,另一种是在具体某一个点处将曲线拆分成两个曲线。
对于前者来说,边线图元类中有一个 .explode_curve 方法可以将边线所属的曲线炸开。这其实有一点点令人费解,打断炸开 Curve 的方法不在 Curve 中。当然也可以自己在 Curve 类中追加一个自定义的方法:
module Sketchupclass Curvedef explode!res=self.edges.to_ares[0].explode_curvereturn resendendend
而对于后者来说, Ruby API 并没有提供直接的方法,比较有效的作法是直接通过绘图区从曲线上引出一条新的边线从而达到打断曲线的目的。如果是使用代码,就需要自己实现了。
以下我提供一个参考的代码:
def point_on_curve?(point,cur)unless point.respond_to?(:on_line?) then raise ArgumentError.new("Param1: Point3d or Array required.") endunless cur.is_a?(Sketchup::Curve) then raise ArgumentError.new("Param2: Curve required.") endreturn cur.edges.any?{|e|e.bounds.contains?(point) and point.on_line?(e.line)}enddef break_curve_at(point,cur)unless point_on_curve?(point,cur) then raise RuntimeError.new("point NOT on the curve.") endes=cur.edges.to_atemp_line=cur.parent.entities.add_line(point,[0,0,0])temp_line.erase!res=es.map(&:curve).uniqend
以下是测试效果:
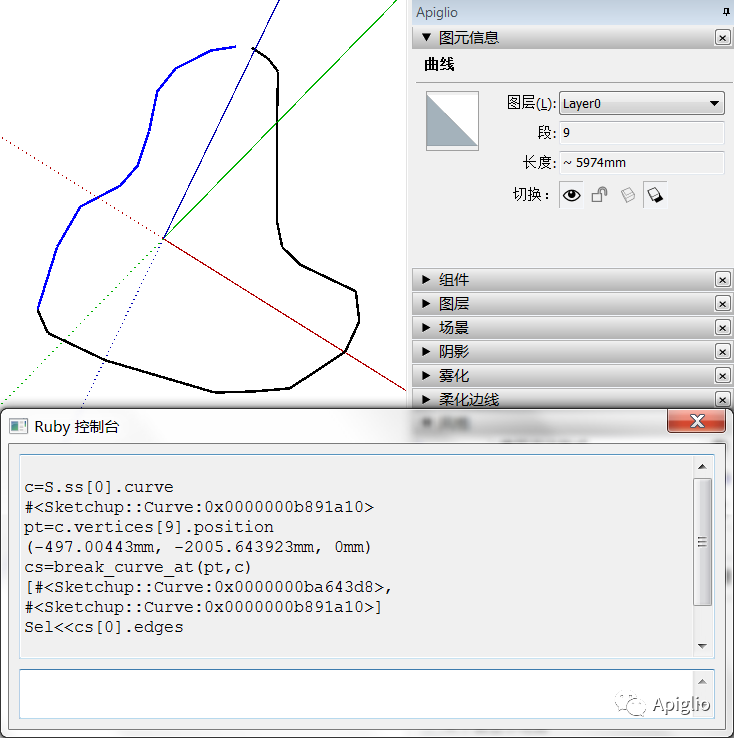
②曲线的续接
两段相连的曲线连接合成为一条曲线在 SU2020.1 版本以前是似乎是无法通过 Ruby API 实现的[注],在新版本中可以使用 Entities 类的 .weld 方法来“暴力”地合并曲线。以下是一个在 SU2021.1 中的测试结果:
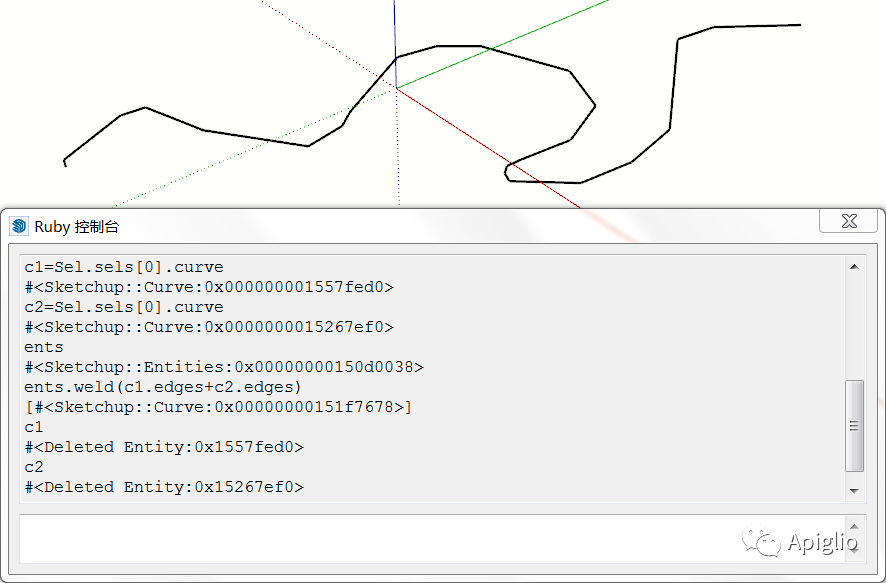
焊接之后,原先的两个曲线概念性图元都会被删除,取而代之的是一个全新的 Curve。
不过圆弧是相对比较特殊的一个存在,它和直线一样,有额外的合并判断规则,这一点使得两段圆弧在满足一定条件的情况下可以通过删除引出的边线合并(或者更好地说法应该是还原)成一个圆弧。这个过程可以理解成:删除边线时边线两端的端点如果满足 .edges.count == 2 则对两个端点的两对边线进行是否可以合并的判断,若是两条共线的直线则删除端点合并直线,若是两条圆心和半径相同的圆弧也相应地合并圆弧。利用这个原理也可以在低版本中实现圆弧的续接,但是意义不大,这里只提及其可能性。
③曲线成面
曲线作为概念性图元,也可以作为 Entities 类中 .add_face 方法的参数,但是使用曲线作为参数创建平面仅在曲线是封闭曲线时有效,否则返回 nil。
ents.add_face curve如果需要使用不封闭的曲线创建平面则要如下表示:
ents.add_face curve.vertices这仅仅是多支持一种参数类型而已,使用曲线类和使用曲线中的所有边线创建的平面图元没有任何差别。
当平面的边缘存在曲线时,其在推拉和路径跟随后,产生的平面会有一些额外的设定,可以解释为曲线中不满足 vertex. curve_interior? != nil 的端点产生了平面中满足 edge. soft? and edge. smooth? 的边线。具体的内容会放在下一篇介绍“表面”图元的教程中。
④自由变换
前文中的曲线编辑都是在既定的规则下,对曲线进行拆分组合,而这个自由变换,可以直接编辑曲线中的每一个点。这个功能需要 Curve 类的 .move_vertices 方法。
以下是官方文档中的示例:
# 此例子来源于官方文档,摘录时有改动# ruby.sketchup.com/Sketchup/Curve.html#move_vertices-instance_methodmodel=Sketchup.active_modelents=model.entitiesnew_edges=ents.add_arc(ORIGIN,X_AXIS,Z_AXIS,20.cm,0,360.degrees,64)curve=new_edges.first.curveface=ents.add_face(new_edges[0].curve.vertices)points=curve.vertices.map(&:position)points.each_with_index{|pt,i|pt.z=i*1.cm}points.each{|pt|puts pt.to_s}curve.move_vertices(points)
执行后的效果如下:
.move_vertices 方法仅接受一串坐标作为它的参数,并且坐标数量与曲线的端点数要求一致,否则就会报错。上述例子中先通过 curve .vertices 方法获得了曲线的所有端点坐标,然后在使用 .each_with_index 迭代器将端点赋予递增的高程。最后将处理后的 points 坐标数组作为参数执行 .move_vertices 方法,便可以依次修改曲线上端点的坐标。
对于 ArcCurve 来说,使用这个方法编辑端点并不会修改它自身创建之初记录的参数,因此调用 .center 之类的方法还会返回原先的数值,包括图元信息窗口也依旧认为这样一个图形是“圆”:
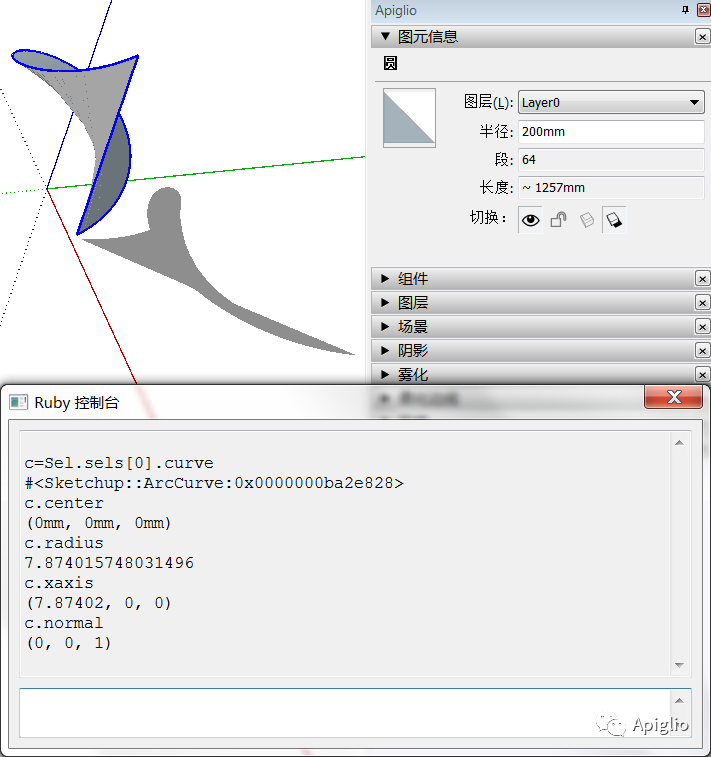
上述例子中在编辑曲线端点之前先根据曲线创建了一个平面,而在移动端点以后,原本的平面发生了变形,破碎成了多个三角面。但是通过选择工具可以一次性点选,并且图元信息窗口会显示这样的结构为“表面”。而这个“表面”,正是曲线之外的另一种概念性图元,会在下一篇中介绍。
注:由于本人比较少接触曲线概念,找了很久也没有发现除了 .weld 方法以外的用 ruby 实现的续接曲线方法,所以教程中我如此描述。当然在老版本中有插件可以实现这个功能,应该是通过 C SDK 实现的,这就不在此教程的讨论范围之内了。
文中在出现过一个随机生成具体个数个随机点坐标的方法,具体的实现过程如下:
def randPts(bounds,times)unless bounds.is_a? Geom::BoundingBox thenraise ArgumentError.new("expected Geom::BoundingBox")endpts=[]for i in 0..times-1 dopts<<[]pts[i]<<bounds.min.x + rand()*bounds.widthpts[i]<<bounds.min.y + rand()*bounds.heightpts[i]<<bounds.min.z + rand()*bounds.depthendreturn(pts)end
(完)
本文编号:SU-R13