Python 内部是如何实现整数相加不溢出的？

说实话昨天的文章划水了，阅读量就是最好的证明。这里读者的水平还是很高的，一看就看出了我的偷懒，标题 Python 的整数有边界么？肯定没有啊，于是就不打开看了。不过今天，我想接着昨天的话题，聊一聊 Python 是如何实现整数相加而不溢出的？

1、如何表示一个整数

要想了解这个，那就需要看 Python 的源代码^[1]，Python中的整数底层对应的结构体是PyLongObject，它位于 longobject.h^[2] 中。

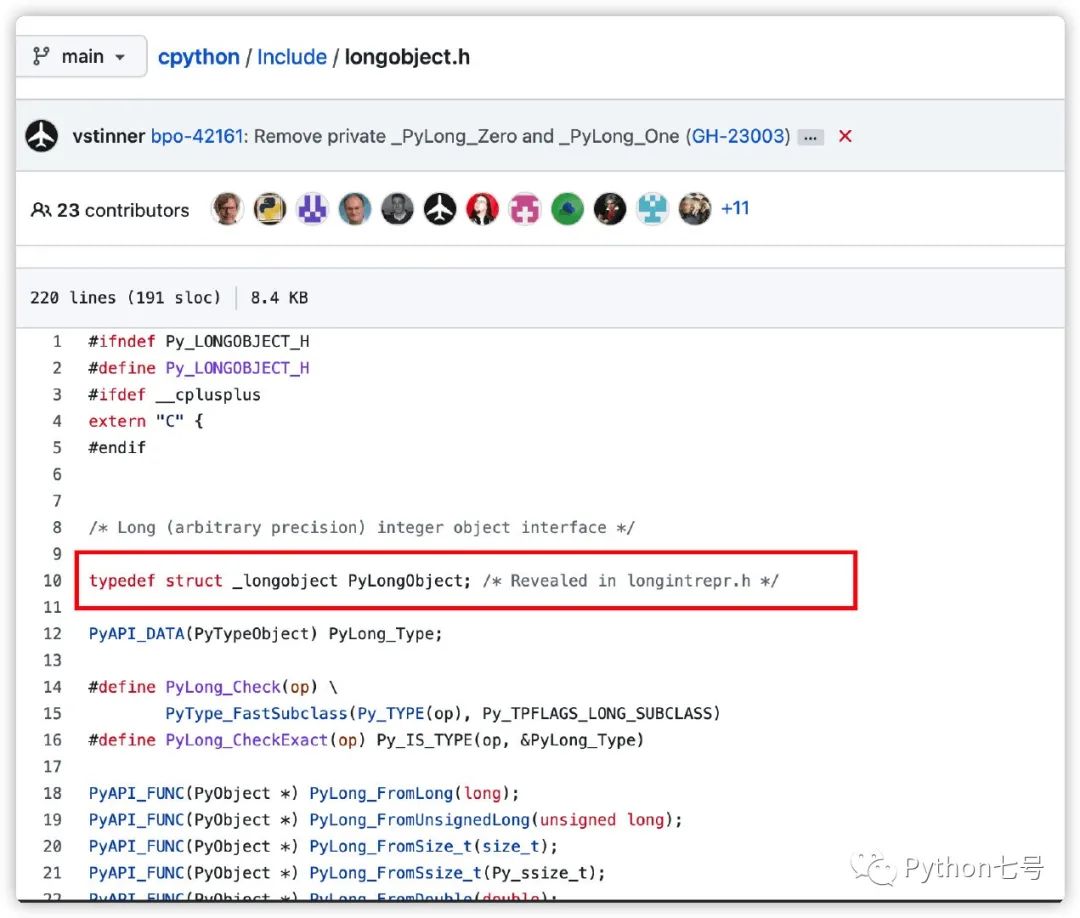
逐步展开如下：

//longobject.h
typedef struct _longobject PyLongObject; /* Revealed in longintrepr.h */
 
//longintrepr.h
struct _longobject {
    PyObject_VAR_HEAD
    digit ob_digit[1];
};
 
//合起来可以看成
typedef struct {
    PyObject_VAR_HEAD
    digit ob_digit[1];
} PyLongObject;

再把宏定义 PyObject_VAR_HEAD 展开：

typedef struct {
    PyObject_HEAD
    int ob_size;
    digit ob_digit[1];
} PyLongObject;

再把宏定义 PyObject_HEAD 展开，结构体中的变量我已经作了注释：

typedef struct {
    int ob_refcnt;    //引用计数
    struct _typeobject *ob_type; //变量类型
    int ob_size;       //用来指明变长对象中一共容纳了多少个元素
    digit ob_digit[1]; //digit类型的数组,长度为1
} PyLongObject;

这里面的 ob_size 用来指明变长对象中一共容纳了多少个元素，也就是 ob_digit 数组的长度，而这个 ob_digit 数组显然只能是用来维护具体的值。

到这里已经很明显了，Python 将大整数切割后存在 ob_digit，这个数组的长度是可变的，数据越大，数组越长，只要内存够用，存多大的数都可以。

那么下面的重点就在这个 ob_digit 数组了，我们看看 Python 中整数对应的值，比如 256，是怎么放在这个数组里面的。不过首先我们要看看这个digit 是个什么类型，它同样定义在 longintrepr.h 中

#if PYLONG_BITS_IN_DIGIT == 30
typedef uint32_t digit;
// ...
#elif PYLONG_BITS_IN_DIGIT == 15
typedef unsigned short digit;
// ...
#endif

PYLONG_BITS_IN_DIGIT 是一个宏，如果你的机器是 64 位的，那么它会被定义为 30，32 位机器则会被定义为 15。

而我们的机器现在基本上都是 64 位的，所以 PYLONG_BITS_IN_DIGIT会等于 30，因为 digit 等价于 uint32_t(unsigned int)，所以它是一个无符号 32 位整型。

所以 ob_digit 这个数组是一个无符号 32 位整型数组，长度为 1。当然这个数组具体多长则取决于你要存储的 Python 整数有多大，因为 C 中数组的长度不属于类型信息，你可以看成是长度 n，而这个 n 是多少要取决于你的整数大小。显然整数越大，这个数组就越长，那么占用空间就越大。

为了说明 256 是如何存放在 ob_digit 里的，我们来简化下，这里假如 ob_digit 这个数组是一个无符号 8 位整型数组，8 位二进制，最大只能表示 255，我们要表示 256，那就只能再申请一个 8 位，也许你认为再申请一个 8 位来表示 1，其实不是的，是使用一个新的 8 位整数来模拟更高的位，如下所示：

255 = [255]
256 = [1,1]

256 = [1,1] 的形式也不是真实情况，为了你理解，先这样写，它表达的意思就是 256 = 1 + 1 * (2^8 - 1) = 1 + 1 * 255 = 256。

也就是说 ob_digit 表示 x 进制数，ob_digit[0] 是低位，ob_digit[1] 是高位，具体 x 是多少，取决于 ob_digit 的类型，这里 8 位，就是 255 进制。

刚才提到 256 = [1,1] 的形式也不是真实情况，因为 PyLongObject 不仅仅是为了存储大整数，也需要参与运算，具体怎么运算呢，那就是 ob_digit 逐位相加即可。

既然是相加，即又可能溢出，比如 [255 , 1] + [255, 1] = [510,2]

这里的 510 就超出了 8 位，为了简化处理，只要我们不用满 8 位，就不会溢出，也就是说，比如说只用 7 位，那最大也就是 [127,...] + [127,...] = [254,...] 也就不会溢出了。

到这里，你会明白，为什么 digit 虽然是无符号 32 位整数，却只使用 30 位了吧：

#if PYLONG_BITS_IN_DIGIT == 30
typedef uint32_t digit;
// ...
#elif PYLONG_BITS_IN_DIGIT == 15
typedef unsigned short digit;
// ...
#endif

聪明的你，可能会问，31 位就可以保证不溢出，为啥牺牲两位，用 30 位，答案我也不知道，可能是因为 64 是 32 的两倍， 30 也是 15 的两倍，这样看起来更舒服吧。

那如何表示负数呢，其实负数的话，就是 ob_size 变成了负的，其他没变。整数的正负号是通过这里的 ob_size 决定的。ob_digit 存储的其实是绝对值，无论 n 取多少，-n 和 n 对应的 ob_digit 是完全一致的，但是ob_size 则互为相反数。所以 ob_size 除了表示数组的长度之外，还可以表示对应整数的正负。

所以 Python 在比较两个整型的大小时，会先比较 ob_size，如果 ob_size 不一样则可以直接比较出大小来。

总结一下，就是当 PYLONG_BITS_IN_DIGIT == 30 的时候，整数 = ob_digit[0] + ob_digit[1] * 2 ** 30 + ob_digit[2] * 2 ** 60 + ...

2、整数占用内存大小

理解了这一点，我们再看一下这个结构体：

typedef struct {
    int ob_refcnt;    //引用计数
    struct _typeobject *ob_type; //变量类型
    int ob_size;       //用来指明变长对象中一共容纳了多少个元素
    digit ob_digit[1]; //digit类型的数组,长度为1
} PyLongObject;

一个整数占用多少个字节，取决于 PyLongObject 这个结构体占用多少字节，ob_refcnt、ob_type、ob_size 这三个是整数所必备的，它们都是 8 字节，加起来 24 字节。所以任何一个整数所占内存都至少 24 字节，至于具体占多少，则取决于 ob_digit 里面的元素都多少个。

现在的你不难理解以下结果：

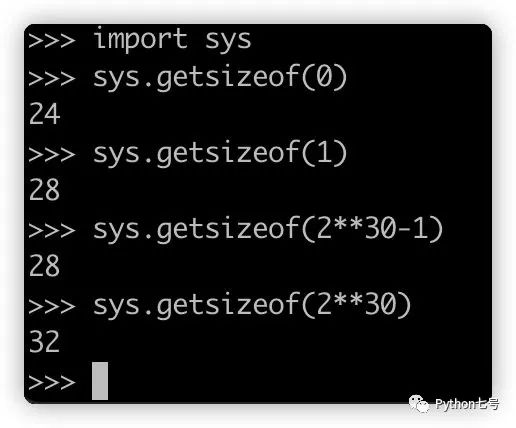
3、整数池

此外 Python 中的整数属于不可变对象，运算之后会创建新的对象:

>>> a = 300
>>> id(a)
140220663619152
>>> a += 1
>>> id(a)
140220663619408
>>>

这样就势必会有性能缺陷，因为程序运行时会有对象的创建和销毁，就是涉及内存的申请和垃圾回收，一个常用的手段就是使用对象池，将频率高的整数预先创建好，而且都是单例模式，需要使用时直接返回。

小整数对象池的实现位于 pycore_interp.h^[3] 中：

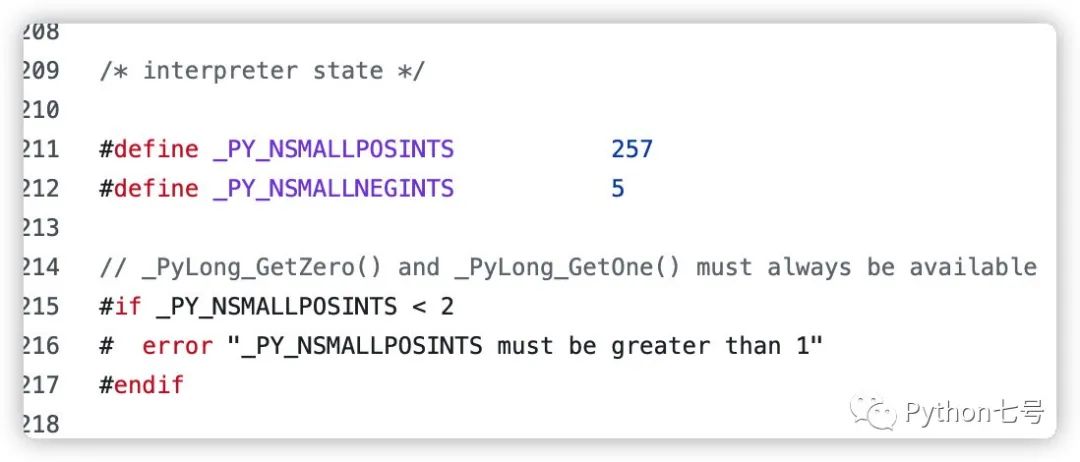
验证一下：

>>> a = -6
>>> b = -6
>>> a is b
False
>>> a = -5
>>> b = -5
>>> a is b
True
>>> a = 256
>>> b = 256
>>> a is b
True
>>> a = 257
>>> b = 257
>>> a is b
False
>>>

不同的版本可能会不同，我这里 Python3.8，区间为 [-5,257)。

4、整数加减法

有了前面的铺垫，现在我们来看下 Python 中大整数是如何相加的，源代码 longobject.c : long_add 函数^[4]

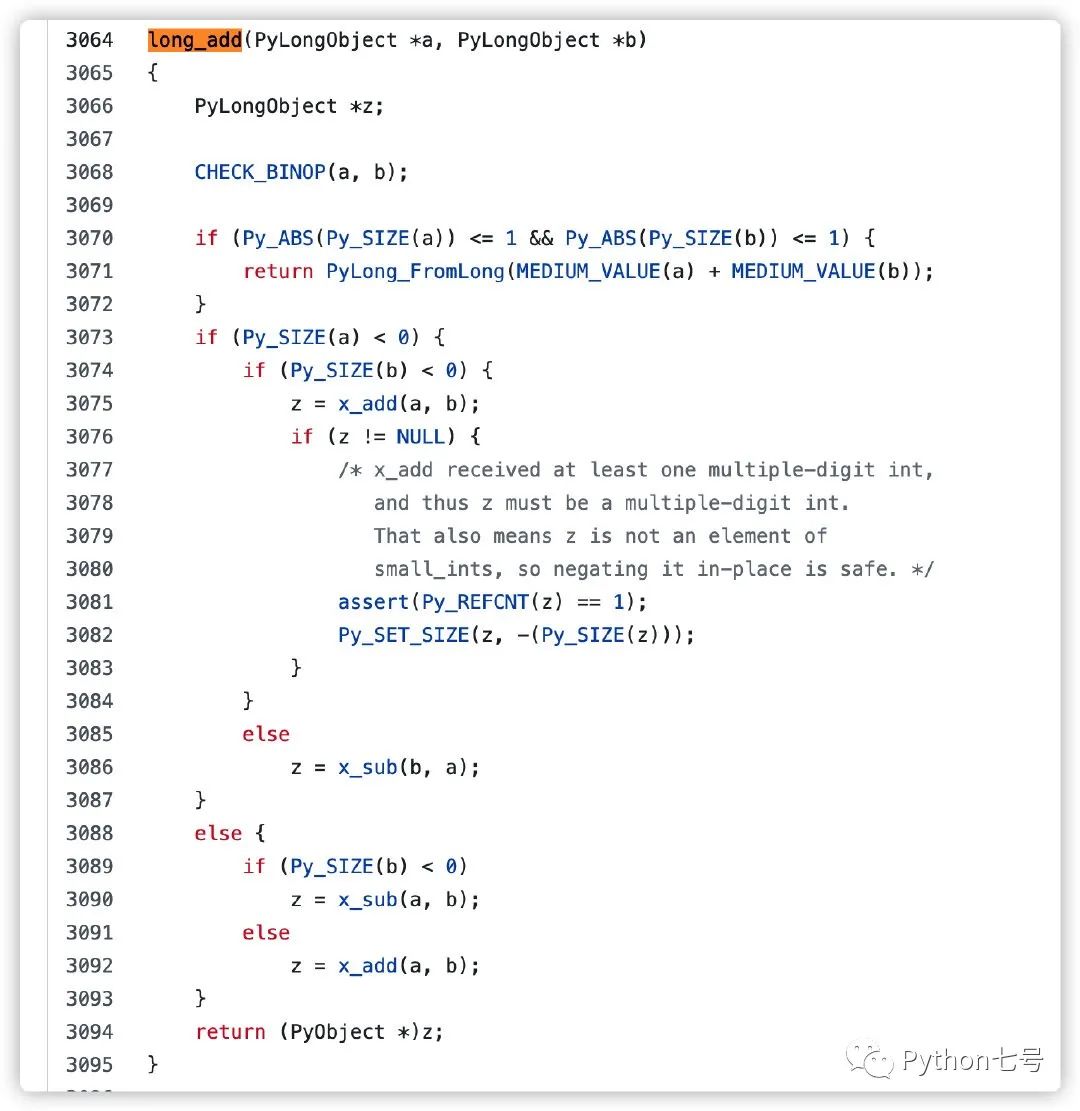
可以看到 long_add 根据 ob_size 的正或负来调用 x_add 或 x_sub。

现在看一下 x_add 的源代码：

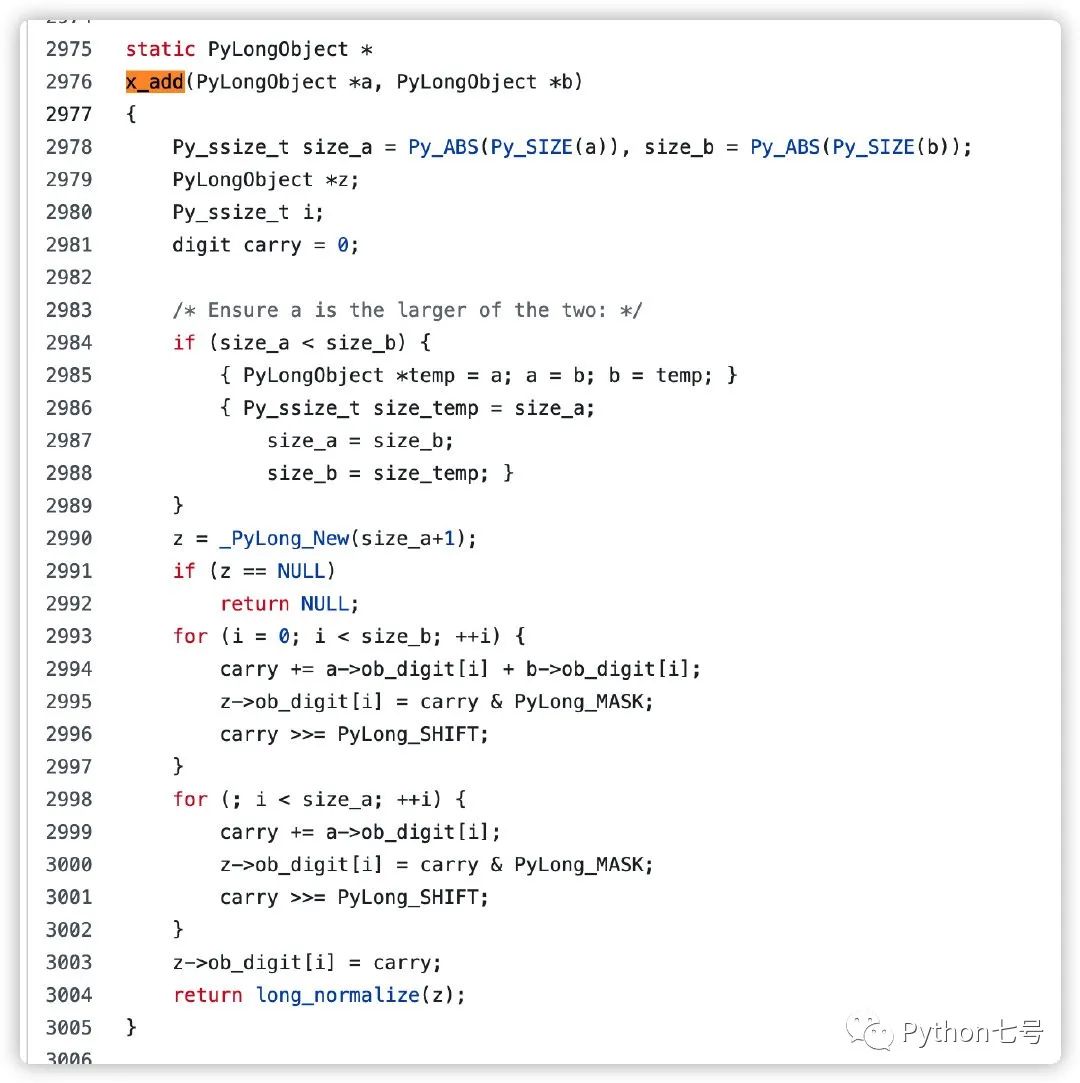
可以看到，Python 大整数的相加就是底层数组的相加，当然还会涉及到进位等操作：

for (i = 0; i < size_b; ++i) {
 carry += a->ob_digit[i] + b->ob_digit[i];
 z->ob_digit[i] = carry & PyLong_MASK;
 carry >>= PyLong_SHIFT;
}

x_sub 的源代码：

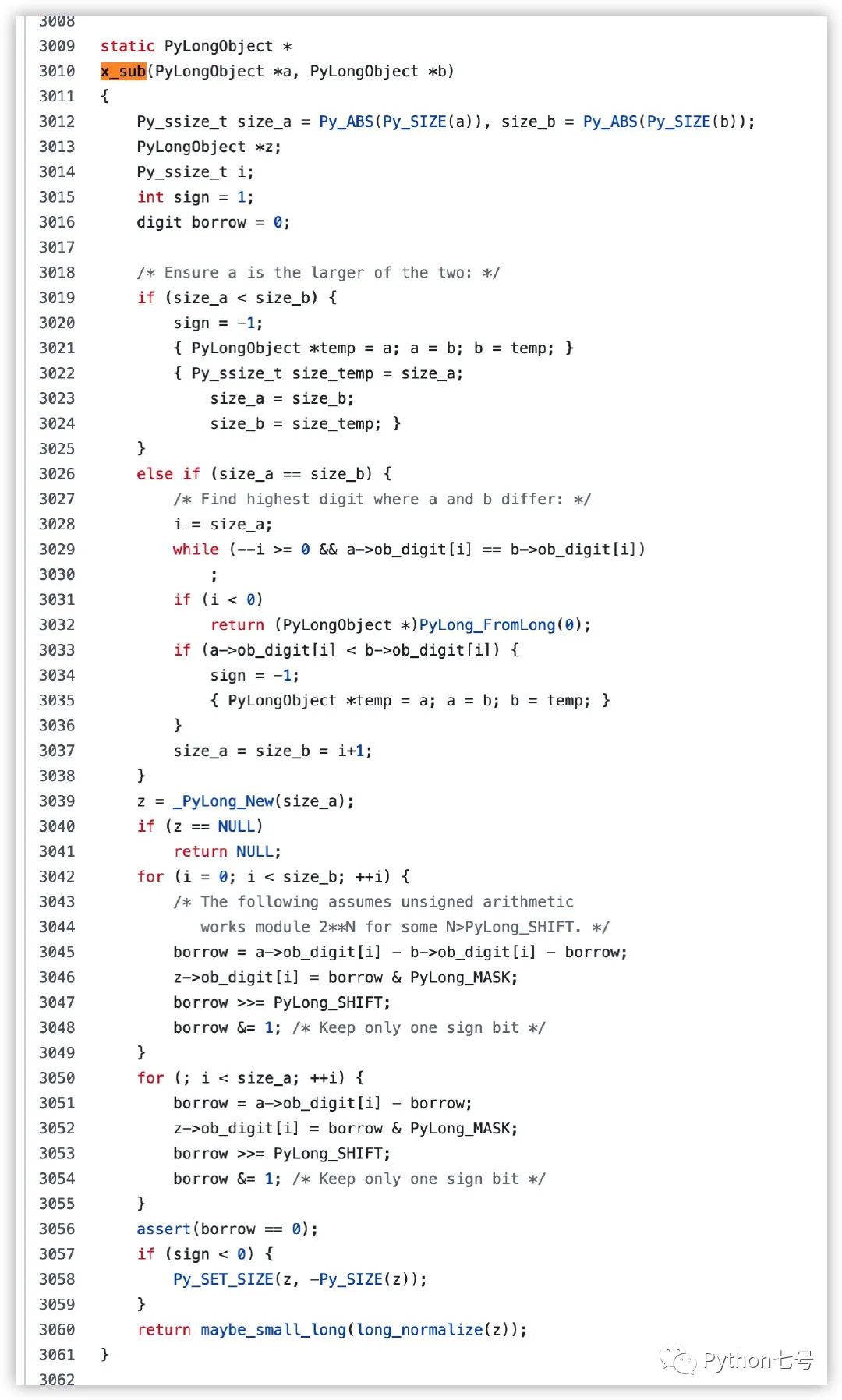
4、整数乘法

Python 整数乘法使用的是 Karatsuba multiplication^[5] 算法进行的大数乘法，感兴趣的可以研究一下。

最后的话

源码之下无秘密，看源码会比较辛苦，却可以学到精髓和本质，本文通过源码逐层展开，带你了解了下 Python 整数对象的实现、整数内存大小的计算，整数池，整数加减法源码，相信你已经知道了 Python 是如何实现整数想加而不溢出的。如果有收获，还请点在、点赞、转发，感谢一路的支持和陪伴。

都看到这里了，你确定不关注一下：

参考资料