概率与随机过程基础
点击下方卡片,关注“新机器视觉”公众号
视觉/图像重磅干货,第一时间送达
转自 | 数学中国
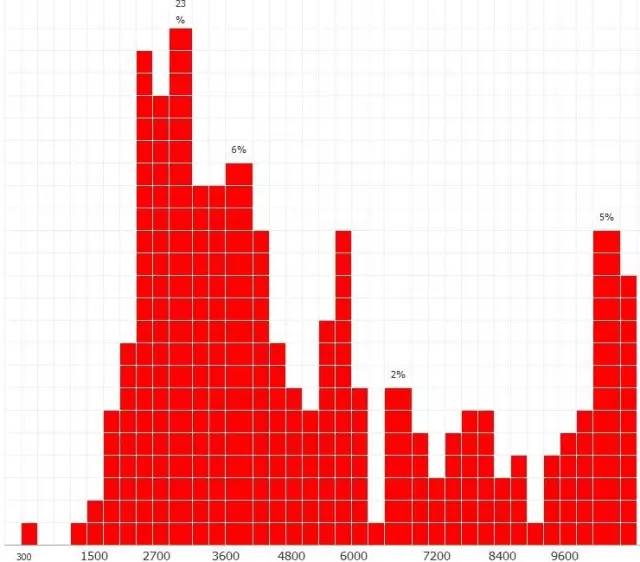
图1. 博文(2009-2013)点击率的直方图:x坐标是点击数, y坐标是在某个点击数范围内的文章数。

图2. x与y的相关性的俯视图
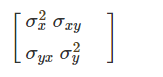
—版权声明—
仅用于学术分享,版权属于原作者。
若有侵权,请联系微信号:yiyang-sy 删除或修改!
评论

点击下方卡片,关注“新机器视觉”公众号
视觉/图像重磅干货,第一时间送达
转自 | 数学中国


—版权声明—
仅用于学术分享,版权属于原作者。
若有侵权,请联系微信号:yiyang-sy 删除或修改!