无人机系列之飞控算法
https://blog.csdn.net/ad3600/article/details/54947073

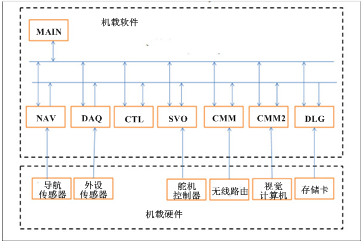
图1 无人机平台构型
多轴飞行器multirotor是一种具有三个以上旋翼轴的特殊的直升机。
旋翼的总距固定而不像一般直升机那样可变。
通过改变不同旋翼相对转速可以改变单轴推进力的大小,从而控制飞行器的运行轨迹。

图5 陀螺仪
加速度传感器

图5 加速计
气压计和超声波

图5 声纳与气压二合一
GPS
图6 GPS示意图
光流
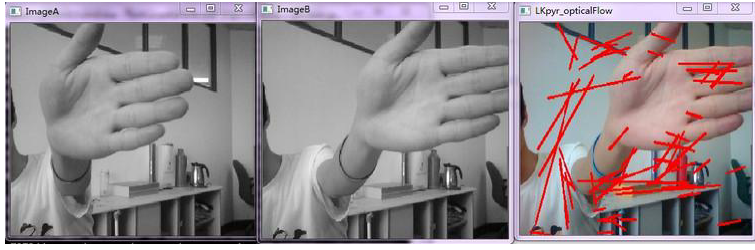
图7 光流算法示意图
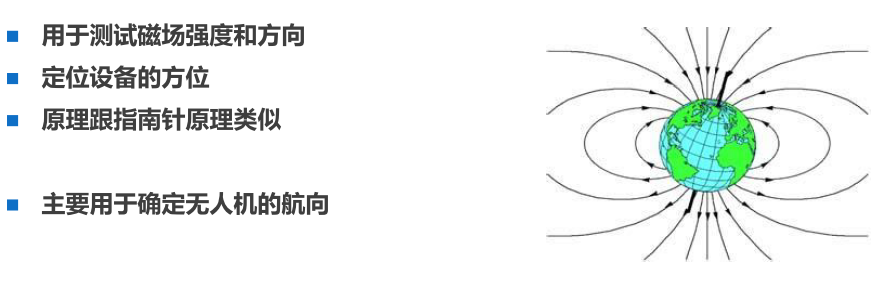
地磁传感器
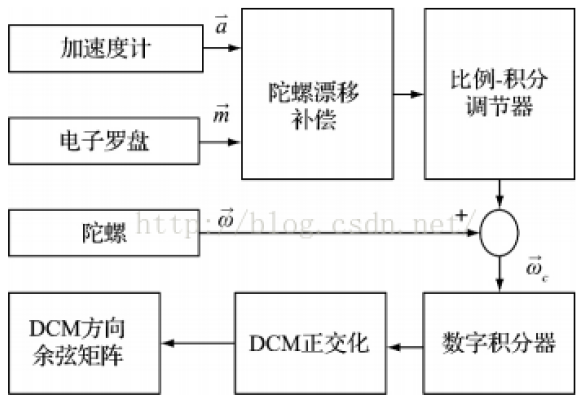
init函数初始化,建立3x3矩阵R。
磁力计修正,得到误差corr:先计算得到误差角度mag_er,再用_wrap_pi函数做约束,再计算corr值,相当于机体坐标系绕地理坐标系N轴(Z轴)转动arctan(mag_earth(1), mag_earth(0))度。
加速度计修正更新误差corr:将陀螺仪计算得到的矩阵第三行(即重力加速度部分)转换到b系,再将加速度测得重力加速度(_accel - 机体加速度)的数据归一化(本身属于b系),将这两个的值进行叉乘即测得误差。
具体过程:归一化的n系重力加速度通过旋转矩阵R左乘旋转到b系,即k为归一化的旋转矩阵R(b-e)的第三行,总的受到合力的方向(_accel)减去机体加速度方向(_pos_acc)得到g的方向,即总加速度(加速度获取)减去机体运动加速度(第五部分)获取重力加速度,然后姿态矩阵的不是行就是列来与纯重力加速度来做叉积,算出误差。
因为运动加速度是有害的干扰,必须减掉。
算法的理论基础是[0,0,1]与姿态矩阵相乘。该差值获取的重力加速度的方向是导航坐标系下的z轴,加上运动加速度之后,总加速度的方向就不是与导航坐标系的天或地平行了,所以要消除这个误差,即“_accel-_pos_acc”。然后叉乘z轴向量得到误差,进行校准 。
对误差corr进行PI控制器中的I(积分),得到_gyro_bias,再对_gyro_bias做约束处理。
使用修正的数据更新四元数,并把_rates和_gyro_bias置零便于下次调用时使用。
获取目标姿态target,并构建目标姿态旋转矩阵。
通过控制四元数获取当前状态的旋转矩阵DCM。
取两个矩阵中的Z轴向量,即YAW-axis。
计算roll,pitch误差,得到误差值e_R:通过R_z%R_sp_z叉乘当前姿态的z轴和目标姿态的z轴的误差大小(即需要旋转的角度)并旋转到b系(即先对齐Z轴)。
计算yaw的权重。
构造e_R_cp反对称矩阵,通过罗德里格公式旋转得到roll,pitch旋转后的矩阵 R_rp。
计算yaw的误差,进一步更新误差值e_R:roll_pitch旋转后的矩阵的x轴
【2】计算e_R_d:
目标姿态旋转矩阵获取四元数。
对四元数的虚部取出赋值给e_R_d,再对其进行归一化处理。
对四元数的实部取出。
计算e_R_d:通过虚部与实部的一系列计算得来。
【3】计算direct_w
【4】进一步更新误差值e_R:通过e_R * (1 - direct_w) + e_R_d * direct_w。
【5】得到_rates_sp角速度变量:对e_R进行p控制,再进行约束