【统计学习方法】 第2章 感知机（一）

 

“这个公众号在我的新作品中帮助我毫不费力地使用了解决万有引力的问题。 我现在有更多时间站在树下，被苹果击中。”

Isaac Newton

感知机是二类分类的线性分类模型，其输入为实例的特征向量，输出为实例的类别。

本章首先介绍感知机模型；然后叙述感知机的学习策略，特别是损失函数；最后介绍感知机学习算法。

感知机是根据输入实例的特征向量  对其进行二分类的线性分类模型，由输入空间到输出空间的如下函数：

其中，    和  为感知机模型的参数，  为权值向量，  叫做偏置。

感知机有如下几何解释，

线性方程，

对应于特征空间的一个超平面，这个超平面将特征空间划分为两个部分。

位于两部分的点（特征向量）分别被分为正、负两类。因此超平面S称为分离超平面。

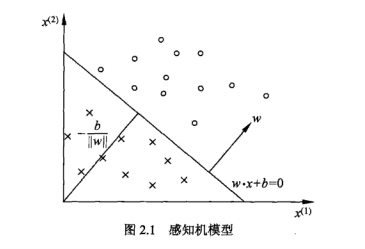
感知机学习，由训练数据集（实例的特征向量及类别）

求感知机模型，即求模型参数  。

感知机学习的目标是求得一个能够将训练集正实例点和负实例点完全正确分开的分离超平面。为了找出这样的超平面，即确定感知机模型的参数  ，需要确定一个学习策略，即定义（经验）损失函数并将损失函数极小化。

极小化损失函数：

显然，损失函数是非负的。如果没有误分类点，损失函数值就是零，而且误分类点越少，误分类点离超平面越近。

感知机学习问题转换为求解损失函数的优化问题，最优化的方法是随机梯度下降法。

随机选取一个误分类点对  进行更新：

式中  （0，1）为步长，在统计学习中又称为学习率。

当实例点被误分类，即位于分离超平面的错误侧，则调整  的值，使分离超平面向该误分类的一侧移动，直到误分类点被正确分类。

这样，通过迭代可以期待损失函数不断减小，直到为0。

扫码关注