图解 | 你管这破玩意叫动态规划
1
全剧终...
2
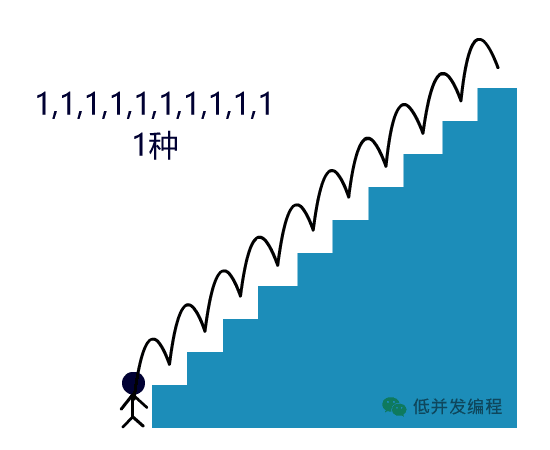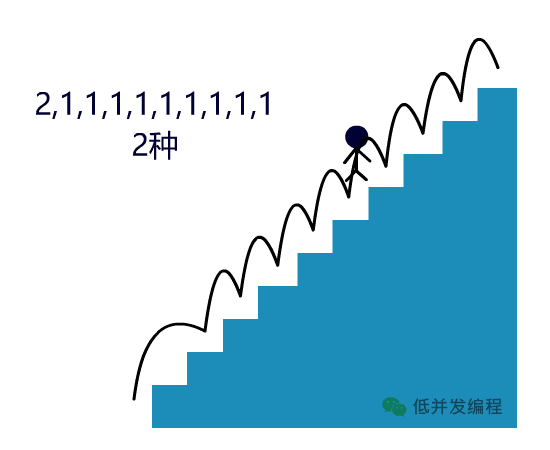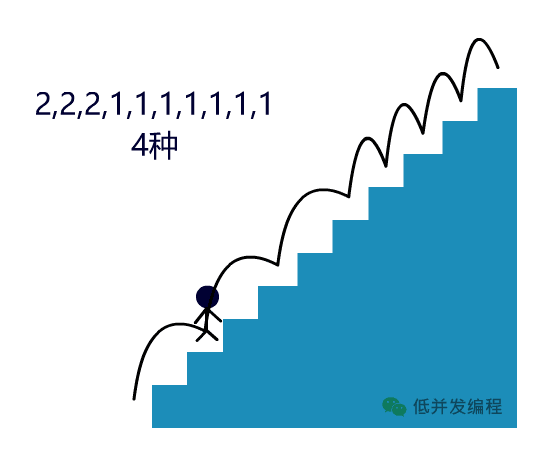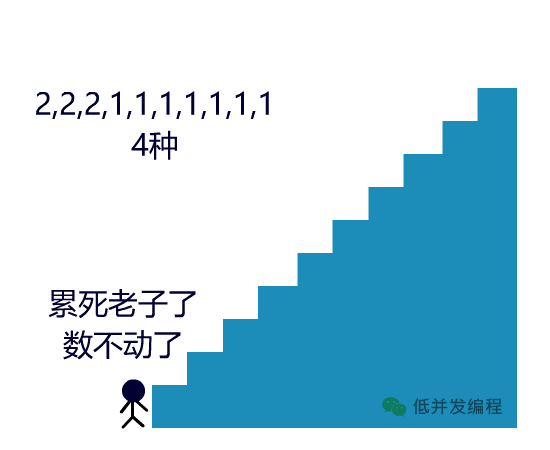

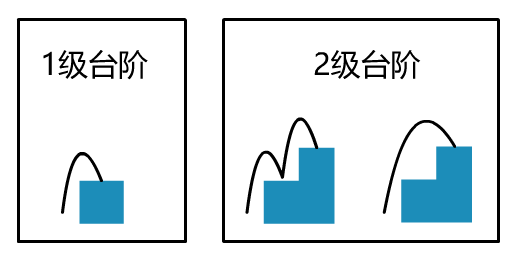
F(x-1) 和 F(x-2) 被称为 F(x) 的最优子结构
F(x) = F(x-1) + F(x-2) 叫状态转移方程
F(1) = 1, F(2) = 2 是问题的边界
int getWays(int n) {
if (n == 1) {
return 1;
}
if (n == 2) {
return 2;
}
return getWays(n-1) + getWays(n-2);
}
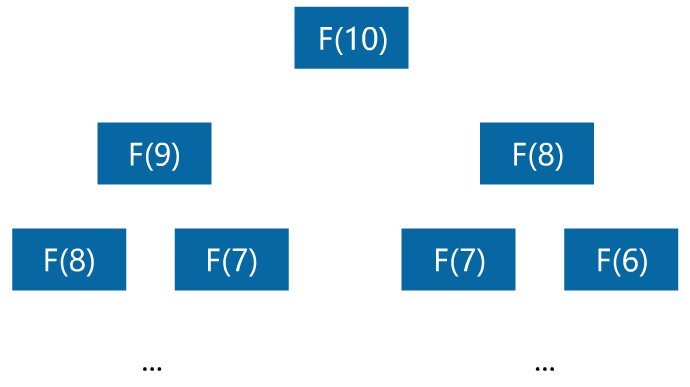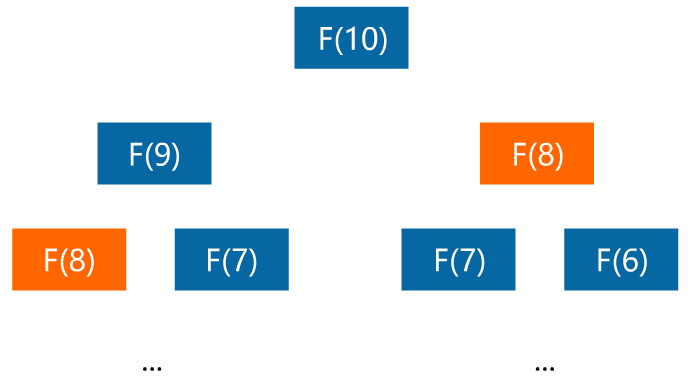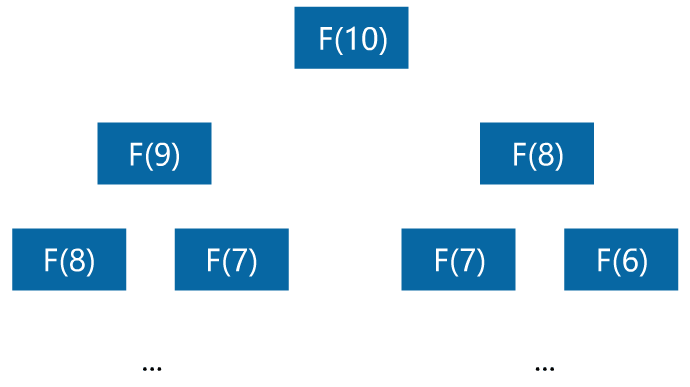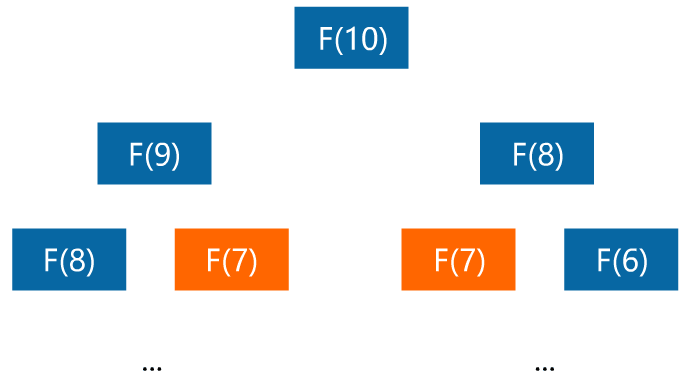
闪客:嗯不错,这样很简洁,但复杂度太高了,是 O(2^n),具体你可以之后想想为什么。现在你看看能不能将复杂度降低。
| 台阶 | 1 | 2 | 3 | 4 | ... | 10 |
| 走法 | a=1 | b=2 | 3 |
| 台阶 | 1 | 2 | 3 | 4 | ... | 10 |
| 走法 | a=2 | b=3 | 5 |
| 台阶 | 1 | 2 | ... | 8 | 9 | 10 |
| 走法 | a=34 | b=55 | 89 |
int getWays2(int n) {
if (n == 1) {
return 1;
}
if (n == 2) {
return 2;
}
int a = 1;
int b = 2;
int temp = 0;
for (int i = 3; i <= n; i++) {
temp = a + b;
a = b;
b = temp;
}
return temp;
}
闪客:不错,这就是这道题正确的动态规划解法,而且时间复杂度是 O(N),空间复杂度是 O(1)
3
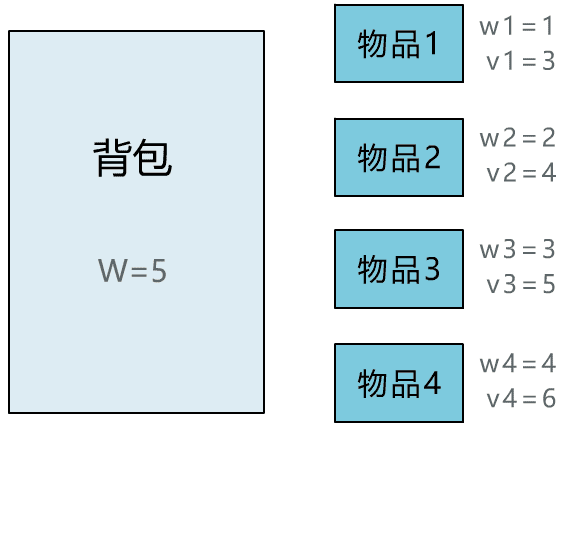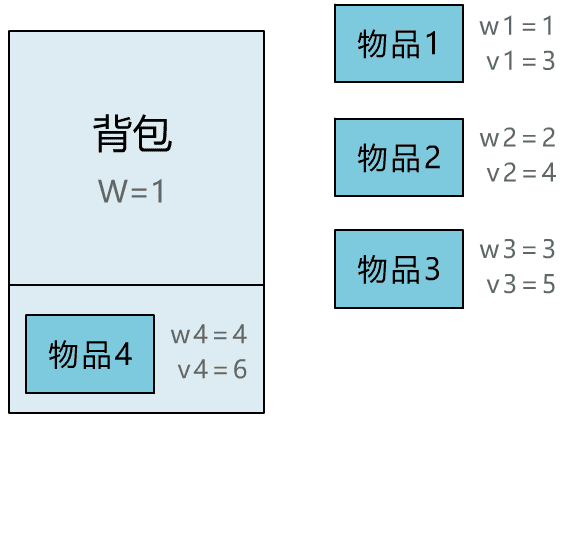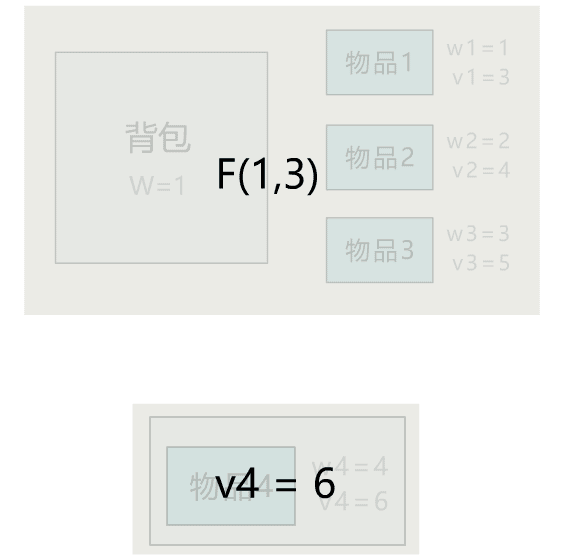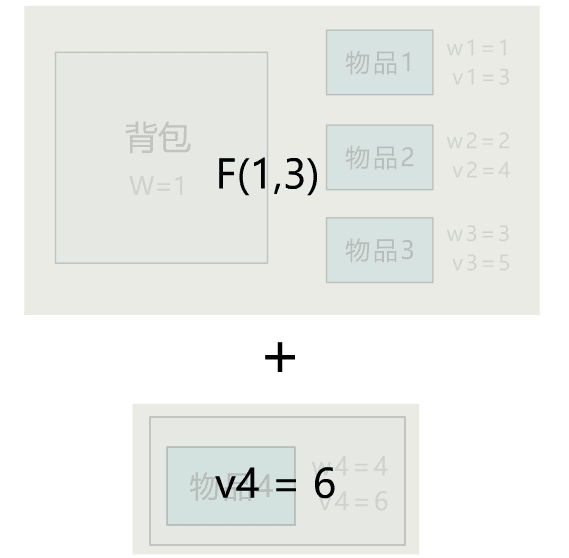
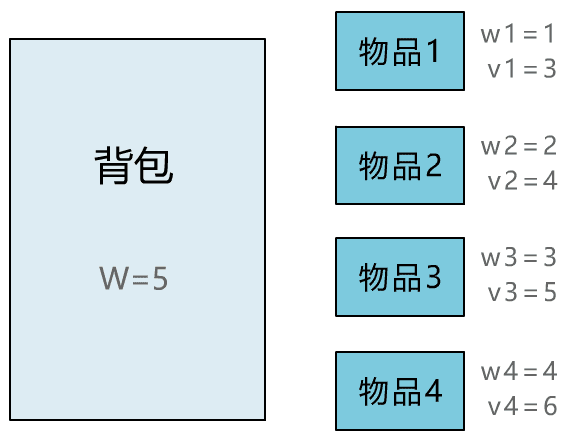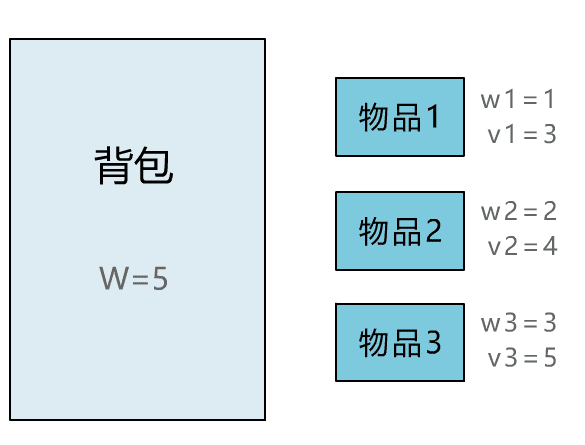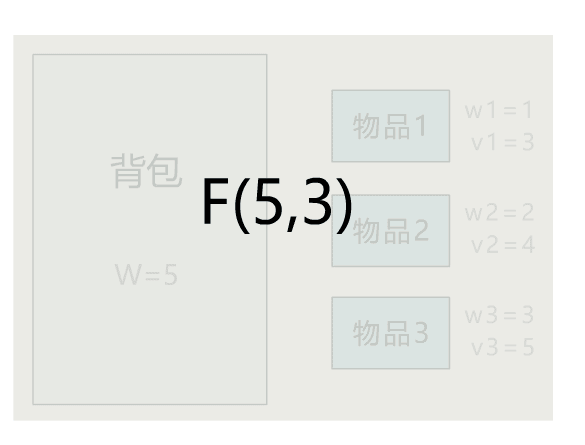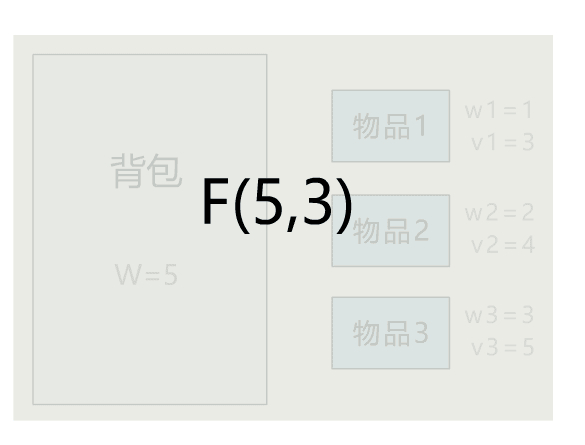
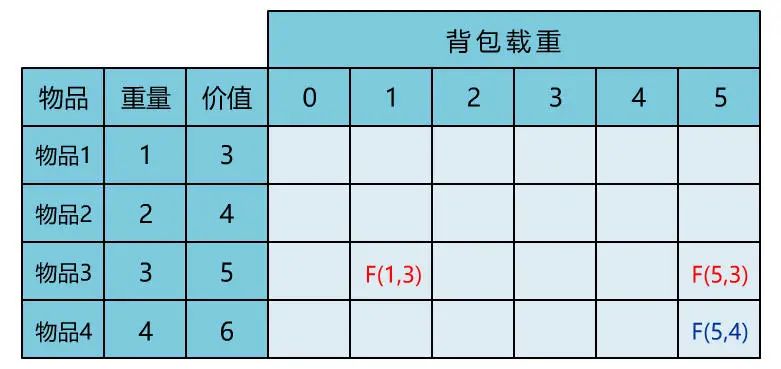
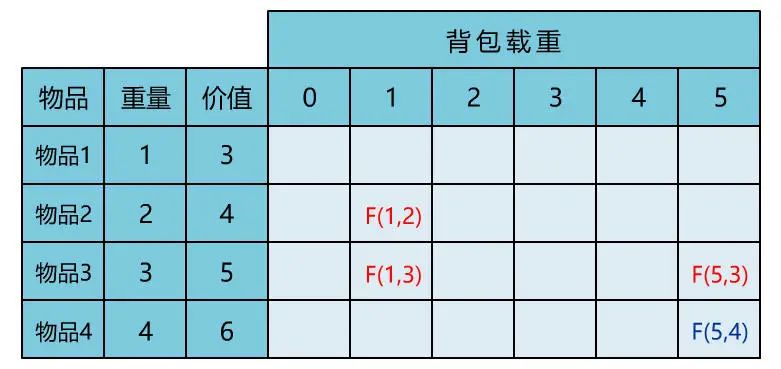
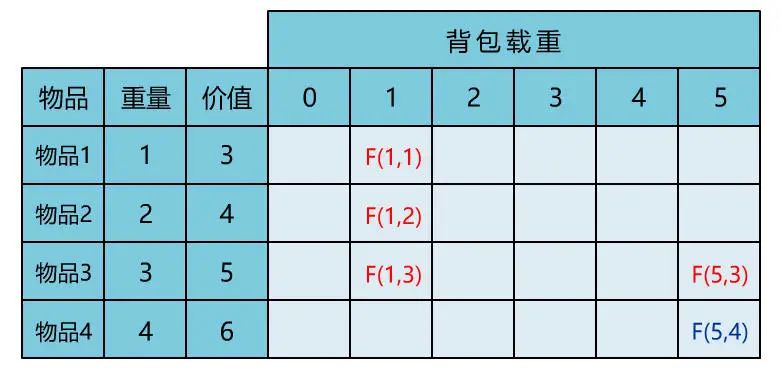
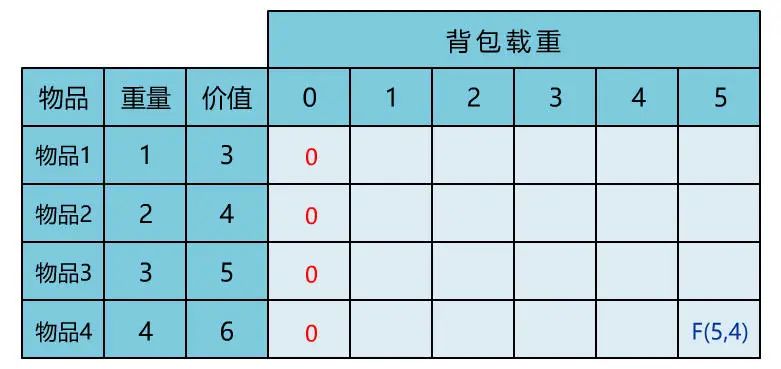
后记
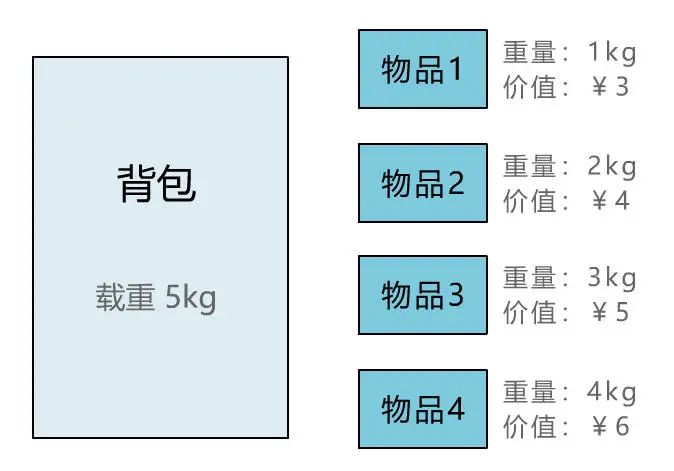
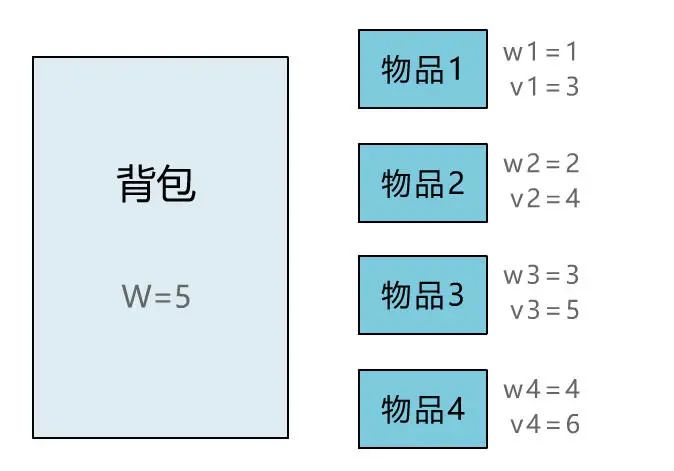
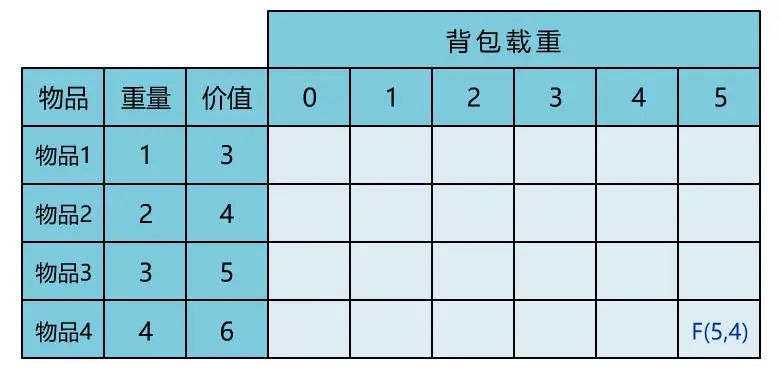
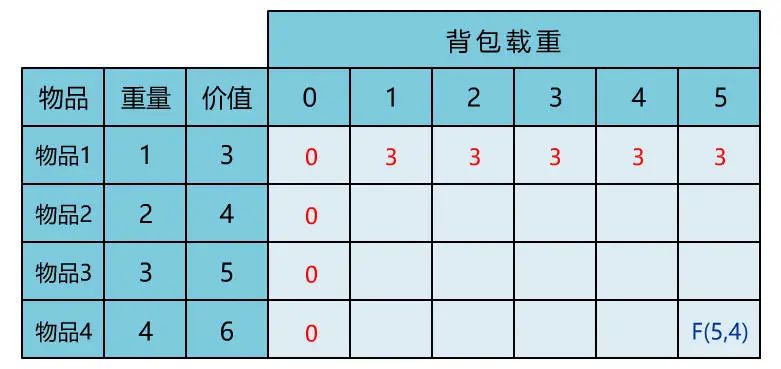
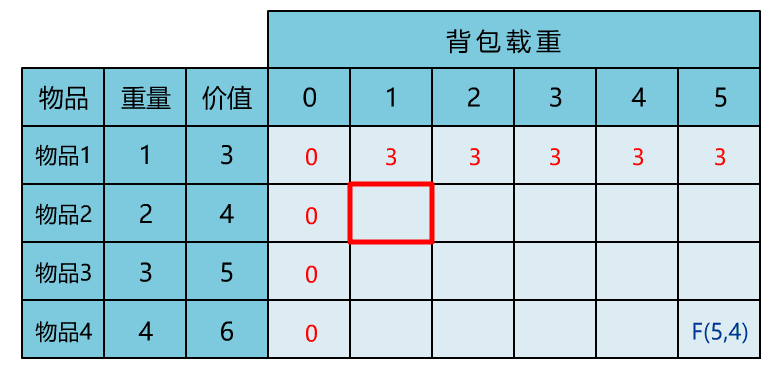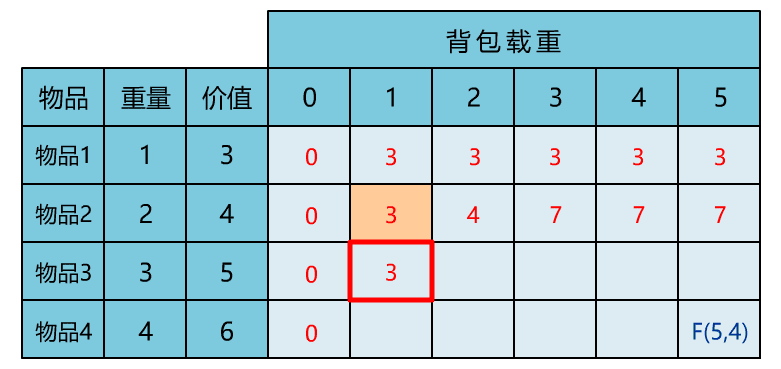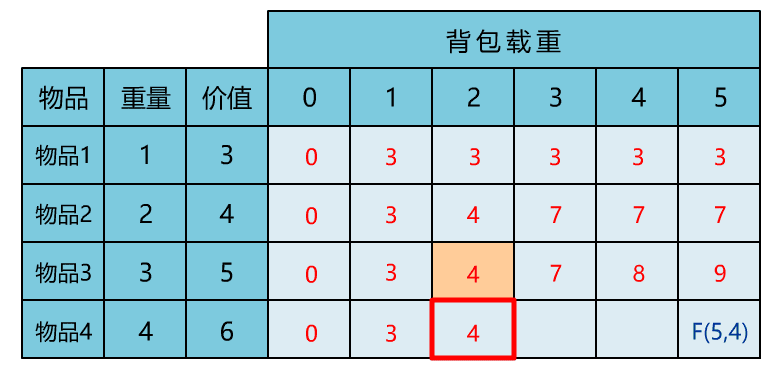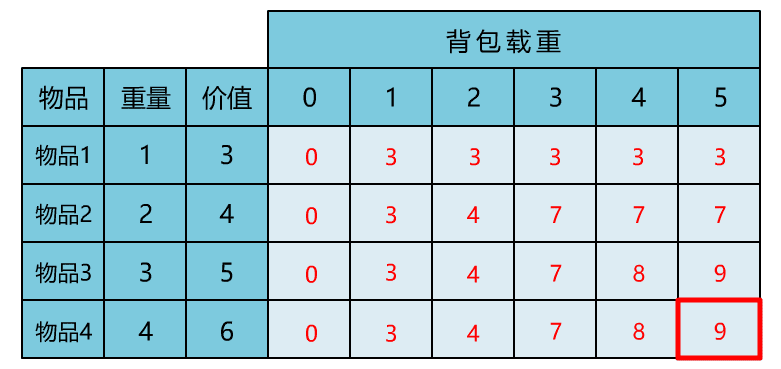
本文通过直观演示 01 背包问题的解题思路,简单说明了动态规划思想的算法核心。可能不少人觉得动态规划难在理解,所以花很多时间在理解其思想上。但其实理解核心思想,这一篇文章就够了,更多的是通过不断做题,反过来帮助自己理解动态规划的思想。所以希望读者在读完本文后,和小宇一样,动手将其代码实现,并找来其他变种题目,继续巩固。
评论
