每日一道 LeetCode (5)：最长公共前缀-轻识

代码仓库

GitHub：https://github.com/meteor1993/LeetCode

Gitee：https://gitee.com/inwsy/LeetCode

题目：最长公共前缀

题目来源：https://leetcode-cn.com/problems/longest-common-prefix/

编写一个函数来查找字符串数组中的最长公共前缀。

如果不存在公共前缀，返回空字符串 ""。

示例 1:

输入: ["flower","flow","flight"]
输出: "fl"

示例 2:

输入: ["dog","racecar","car"]
输出: ""
解释: 输入不存在公共前缀。

说明:

所有输入只包含小写字母 a-z 。

解题思路 A ：「暴力横向查找」

看到这道题，我又感觉我行了，先聊聊我没看答案之前的思路，这个思路我觉得是一个正常人，看到这道题应该有的，如果这个思路都没有，可能你比较适合学文科。

我的思路一般都很暴力，直接循环这个字符串数组，从第一个开始，挨个向后比较，比较两个字符串的每一个字符，遇到不一样的直接返回。

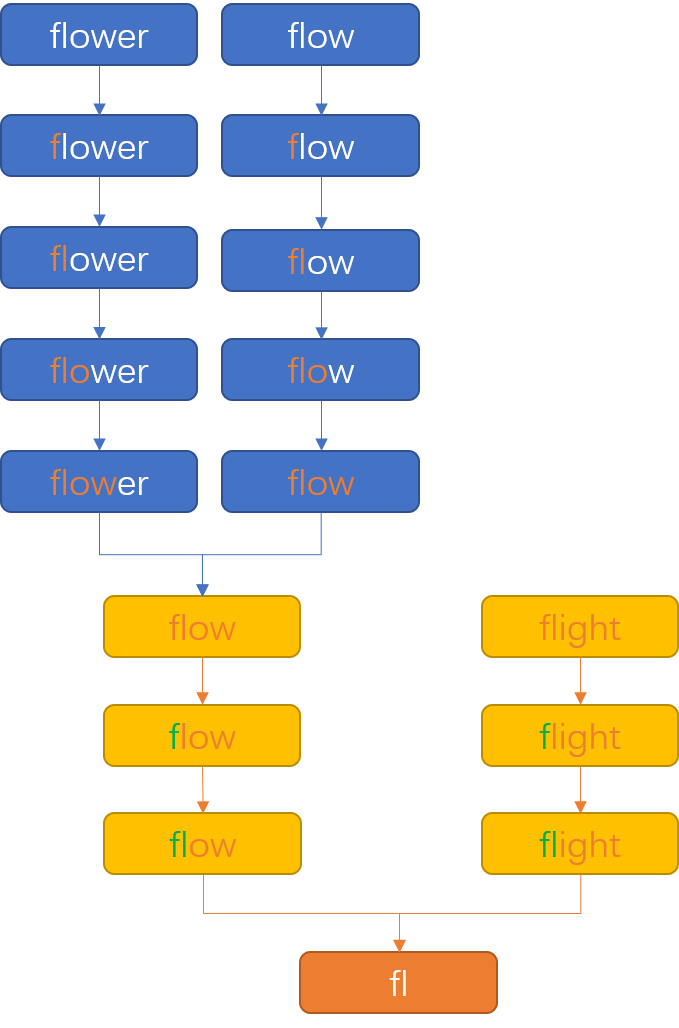
这思路够简单、暴力、直接吧，我想大家第一反应应该都能想得到这个方案。

接下来是代码时间：

public String longestCommonPrefix(String[] strs) {

    if (strs.length == 0) return "";

    String prefix = strs[0];

    for (int i = 1; i < strs.length; i++) {
        prefix = compareTwoStrs(prefix, strs[i]);
        if (prefix.length() == 0) break;
    }

    return prefix;
}

// 获取两个字符串的公共前缀
private String compareTwoStrs(String str1, String str2) {
    int length = Math.min(str1.length(), str2.length());
    int index = 0;
    while (index < length && str1.charAt(index) == str2.charAt(index)) {
        index++;
    }
    return str1.substring(0, index);

}

我在 LeetCode 上运行了一下，直接得到这个结果，这个结果应该是我做 LeetCode 最好的结果了，竟然耗时小于 1ms ，难道我已经这么牛皮了么，我感觉自己飘了。

我满怀信心的打开了答案页，正准备写个回答装个 B 的时候，我傻眼了， NM ，这道题竟然有这么多种解法的啊，心态崩了啊。

忽然想到，刚才我的方案只是一个最简单的正向暴力破解的方案，但是我的解法耗时低于 1ms 啊，这么看来，我的解法还是可以的嘛。

解题思路 B ：「暴力纵向查找」

我看到答案上把我上面的那种思路叫做「暴力横向查找」，然后大神们按照这个思路，又搞出来了「暴力纵向查找」。

图我就不画了，反正和上面的思路一致，就是把横向比较换成了纵向比较，然后一个接一个比一圈，直到最短的字符串长度结束，或者开始出现不一样的字符为止。

代码涨这个样子：

public String longestCommonPrefix_1(String[] strs) {
    if (strs.length == 0) return "";
    for (int i = 0; i < strs[0].length(); i++) {
        for (int j = 1; j < strs.length; j++) {
            if (i == strs[j].length() || strs[j].charAt(i) != strs[0].charAt(i)) {
                return strs[0].substring(0, i);
            }
        }
    }
    return strs[0];
}

解题思路 C ：「分治」

当我以为到这里就结束了的时候，我接着往下翻了翻答案，结果发现我自己还是图样图森破啊，我太小看了「学霸」和「大神」这两个词。

「分治」这个方案是先把字符串数组从中间切开，然后再按照「暴力横向查找」的方案分别取到切开后的两个数组的最长前缀，最后再从这两个前缀中取交集。

这种方案可以看做是「暴力横向查找」方案的一个变种方案，示意图如下：

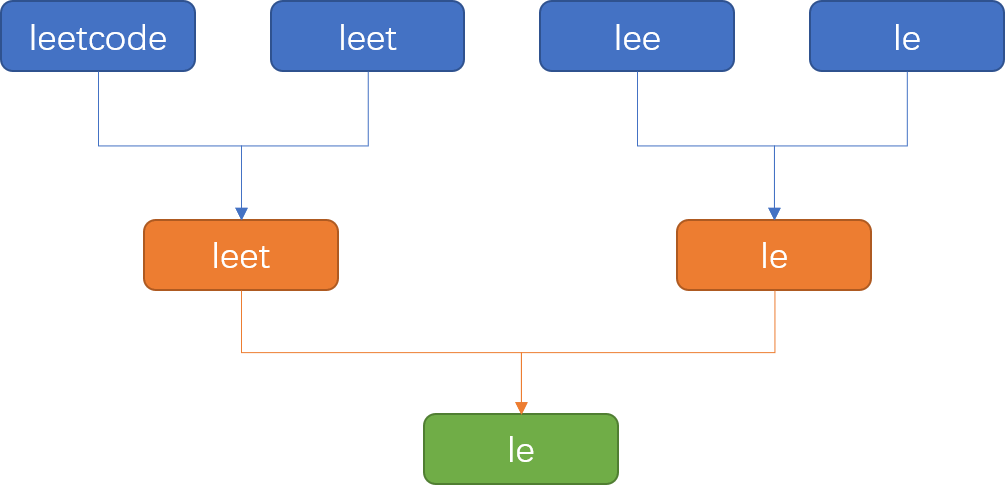
public String longestCommonPrefix_2(String[] strs) {
    if (strs.length == 0) {
        return "";
    } else {
        return longestCommonPrefix(strs, 0, strs.length - 1);
    }
}

public String longestCommonPrefix(String[] strs, int start, int end) {
    if (start == end) {
        return strs[start];
    } else {
        int mid = (end - start) / 2 + start;
        String lcpLeft = longestCommonPrefix(strs, start, mid);
        String lcpRight = longestCommonPrefix(strs, mid + 1, end);
        return commonPrefix(lcpLeft, lcpRight);
    }
}

public String commonPrefix(String lcpLeft, String lcpRight) {
    int minLength = Math.min(lcpLeft.length(), lcpRight.length());
    for (int i = 0; i < minLength; i++) {
        if (lcpLeft.charAt(i) != lcpRight.charAt(i)) {
            return lcpLeft.substring(0, i);
        }
    }
    return lcpLeft.substring(0, minLength);
}

当然，这种方案还可以接着变种，把「暴力横向查找」替换成「暴力纵向查找」。

解题思路 D ：「二分查找」

最后还有一种二分查找比较新奇，我觉得刷题少的人肯定想不到这种方案。

这种方案的思路是在字符串数组中，最长公共前缀的长度肯定不会超过字符串数组中的最短字符串的长度（如果超过了，也不会是最长公共前缀）。

首先找到最短的字符串长度 minLength ，然后随机找一个字符串判断这个 minLength 是否是最长公共前缀，如果不是则把这个 minLength 从中间劈开，接着判断前一半是不是公共前缀，如果是，则最长公共前缀一定大于等于这一半，如果不是，则最长公共前缀一定小于这一半，就这样逐渐缩小范围，直到找到为止。

这个我就不画图了，就是一个单纯的二分法不停的往下切，直到切中了为止。

public String longestCommonPrefix_3(String[] strs) {
    if (strs.length == 0) return "";
    // 先获取最小长度
    int minLength = Integer.MAX_VALUE;
    for (String str : strs) {
        minLength = Math.min(minLength, str.length());
    }

    // 定义变量，开始二分法
    int low = 0, high = minLength;
    while (low < high) {
        // 获取中间点
        int mid = (high - low + 1) / 2 + low;
        if (isCommonPrefix(strs, mid)) {
            low = mid;
        } else {
            high = mid - 1;
        }
    }
    return strs[0].substring(0, low);
}

public Boolean isCommonPrefix(String[] strs, int length) {
    // 先获取前一半要比较的字符串
    String str0 = strs[0].substring(0, length);
    for (int i = 1; i < strs.length; i++) {
        for (int j = 0; j < length; j++) {
            // 按字符进行判断，如果有不一样的字符直接返回 false
            if (str0.charAt(j) != strs[i].charAt(j)) {
                return false;
            }
        }
    }
    return true;
}

从上面的结果看下来，好像是二分法的速度是最慢的，实际上这是由于测试的数据集的关系，测试所使用的的数据集可能都比较适合「暴力横向查找」这个方案。

感谢阅读