2021年,我终于决定入门GCN
共 6480字,需浏览 13分钟
·
2021-03-25 21:07

「前情提要」
💘背景
“你别过来呀!”
“怎么了?好兄弟👬 干嘛这么害怕 😄”
“......能不能安生点?每次都是有事!”
“😈上次海底捞的味道 不好吃么!”
“那不是!还想着再去一次(回味态,啧啧啧)”
“可以呀,感谢你帮我这么多,要不然我把妹的机会早就错过了,感谢感谢🤝”
“没事,不用太客气了,哈哈”
“那我们定个时间,这周日,怎么样?”
“可以呀,正好我俩可以好好侃侃!”
“对了,你对这两天‘新疆棉花’事件怎么看?”
“那肯定是抵制那些企业了!”
“能不能结合计算机学科特点和当前的事和我讲一讲这件事?”
 “(这小子可以呀,这么套路!),好的,我给你说下基本策略,剩下的你自己去融会贯通!”
“(这小子可以呀,这么套路!),好的,我给你说下基本策略,剩下的你自己去融会贯通!”
“😕,那......也行吧”
“记住,我只说一遍!”
什么是GCN
由于高度的复杂性和信息的结构特征,图上的机器学习是一项困难的任务。「GCN是被设计用来针对图结构的神经网络,它能从之前的网络层中聚合信息。在图中,这种机制能够对节点产生有用的特征表示。」
GCN是基于图机器学习的非常强大的神经网络体系结构。
实际上,它们是如此强大,以至于随机发起的2层GCN都可以产生网络中节点的有用特征表示。
下图说明了由此类GCN生成的网络中每个节点的二维表示。请注意,即使没有任何训练,网络中节点的相对接近度仍保留在二维表示中。
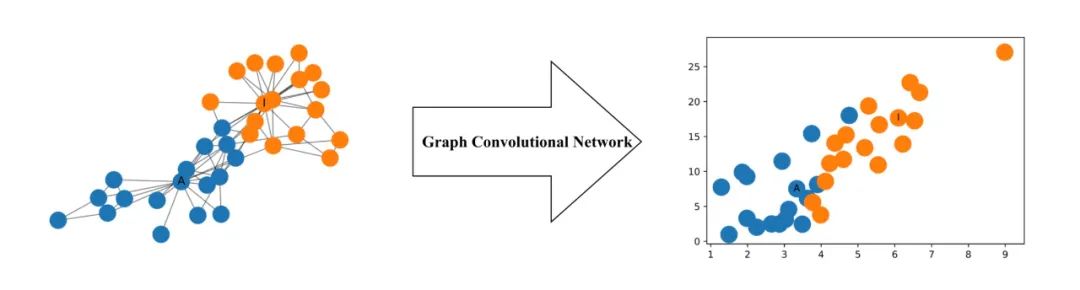
更正式地说,图卷积网络(GCN)是在图上运行的神经网络。给定图G =(V,E),V表示节点,E表示边,则GCN作为输入 输入特征矩阵X(N×F⁰),其中N是节点数,F⁰是每个节点的输入特征数,以及图结构的N×N矩阵表示形式,例如G的邻接矩阵A
因此,GCN中的隐藏层可以写成Hⁱ= f(Hⁱ⁻¹,A))。
其中H⁰= X,f是传播(propagation)方式。每一层Hⁱ对应于一个N×Fi特征矩阵,其中每一行是一个节点的特征表示。在每一层,使用传播规则f聚合这些特征,以形成下一层的特征。这样,特征在连续层上变得越来越抽象。在此框架中,GCN的变体仅在传播规则f的选择上有所不同。
一个简单的传播规则
传播规则中最简单的一种是:
f(Hⁱ,A)=σ(AHⁱWⁱ)
其中Wⁱ是第i层的权重矩阵,而σ是非线性激活函数,例如ReLU函数。权重矩阵的尺寸为Fⁱ×Fⁱ⁺¹;换句话说,权重矩阵的第二维的大小确定了下一层的特征数量。如果你熟悉卷积神经网络,则此操作类似于过滤操作(filtering operation),因为这些权重在图中的节点之间共享。
简化
让我们从最简单的角度检查传播规则:
i = 1,满足 f是输入特征矩阵的函数 σ是恒等函数 选择权重 AH⁰W⁰=AXW⁰= AX
换句话说,f(X,A)= AX。这个传播规则可能有点太简单了,稍后我们会添加缺失的部分。AX现在等效于多层感知器的输入层。
一个简单的图形示例
举一个简单的例子,我们使用以下图形:

下面是其numpy邻接矩阵表示形式。
A = np.matrix([
[0, 1, 0, 0],
[0, 0, 1, 1],
[0, 1, 0, 0],
[1, 0, 1, 0]],
dtype=float
)
接下来,根据其索引为每个节点生成2个整数特征,便于以后手动确认矩阵计算。
In [3]: X = np.matrix([
[i, -i]
for i in range(A.shape[0])
], dtype=float)
X
Out[3]: matrix([
[ 0., 0.],
[ 1., -1.],
[ 2., -2.],
[ 3., -3.]
])
应用传播规则
好吧!现在,我们有了一个图形,其邻接矩阵A和一组输入要素X。让我们看看应用传播规则时会发生什么:
In [6]: A * X
Out[6]: matrix([
[ 1., -1.],
[ 5., -5.],
[ 1., -1.],
[ 2., -2.]]
发生了什么?现在,每个节点(每行)的表示形式都是其邻居特征的总和!换句话说,图卷积层将每个节点表示为其邻居的集合。注意,在这种情况下,如果存在从v到n的边,则节点n是节点v的邻居。
问题
你可能已经发现了问题:
节点的汇总表示不包括其自身的功能!
该表示是邻居节点特征的集合,因此只有具有自环的节点才会在集合中包括自己的特征。度数较大的节点的特征将具有较大的值,而度数较小的节点将具有较小的值。这可能会导致梯度消失或爆炸,但对于随机梯度下降算法(通常用于训练此类网络并且对每个输入特征的比例(或值的范围)敏感)也存在问题。在下文中,我将分别讨论每个问题。
添加自环
为了解决第一个问题,可以简单地向每个节点添加一个自环。实际上,这是通过在应用传播规则之前将单位矩阵I与邻接矩阵A相加来完成的。
In [4]: I = np.matrix(np.eye(A.shape[0]))
IOut[4]: matrix([
[1., 0., 0., 0.],
[0., 1., 0., 0.],
[0., 0., 1., 0.],
[0., 0., 0., 1.]
])
In [8]: A_hat = A + I
A_hat * X
Out[8]: matrix([
[ 1., -1.],
[ 6., -6.],
[ 3., -3.],
[ 5., -5.]])
由于该节点现在是其自身的邻居,因此在总结其邻居的特征时会包括该节点自己的特征!
规范特征表示
通过将邻接矩阵A与D的逆矩阵相乘来变换邻接矩阵A,可以按节点度对特征表示进行归一化。因此,我们简化的传播规则如下所示:
f(X,A)=D⁻¹AX
让我们看看发生了什么。我们首先计算度矩阵。
In [9]: D = np.array(np.sum(A, axis=0))[0]
D = np.matrix(np.diag(D))
D
Out[9]: matrix([
[1., 0., 0., 0.],
[0., 2., 0., 0.],
[0., 0., 2., 0.],
[0., 0., 0., 1.]
])
在应用规则之前,让我们看看对邻接矩阵进行转换后会发生什么。
Berfore
A = np.matrix([
[0, 1, 0, 0],
[0, 0, 1, 1],
[0, 1, 0, 0],
[1, 0, 1, 0]],
dtype=float
)After
In [10]: D**-1 * A
Out[10]: matrix([
[0. , 1. , 0. , 0. ],
[0. , 0. , 0.5, 0.5],
[0. , 0.5, 0. , 0. ],
[0.5, 0. , 0.5, 0. ]
])
请注意,邻接矩阵每一行中的权重(值)已除以与该行相对应的节点的度。我们将传播规则与变换后的邻接矩阵一起应用:
In [11]: D**-1 * A * X
Out[11]: matrix([
[ 1. , -1. ],
[ 2.5, -2.5],
[ 0.5, -0.5],
[ 2. , -2. ]
])
得到与相邻节点特征均值相对应的节点表示。这是因为(转换后的)邻接矩阵权重,与相邻节点特征加权和的权重相对应。我鼓励你自己验证此观察。
放在一起
现在,我们结合了自循环和标准化技巧。此外,我们将重新介绍先前为简化讨论而丢弃的权重和激活函数。
加重权重
首要任务是应用权重。请注意,这里D_hat是A_hat = A + I的度矩阵,即具有强制自环的A的度矩阵。
In [45]: W = np.matrix([
[1, -1],
[-1, 1]
])
D_hat**-1 * A_hat * X * W
Out[45]: matrix([
[ 1., -1.],
[ 4., -4.],
[ 2., -2.],
[ 5., -5.]
])
如果我们想减小输出特征表示的维数,可以减小权重矩阵W的大小:
In [46]: W = np.matrix([
[1],
[-1]
])
D_hat**-1 * A_hat * X * W
Out[46]: matrix([[1.],
[4.],
[2.],
添加激活功能
我们选择保留特征表示的维数并应用ReLU激活功能。
In [51]: W = np.matrix([
[1, -1],
[-1, 1]
])
relu(D_hat**-1 * A_hat * X * W)
Out[51]: matrix([[1., 0.],
[4., 0.],
[2., 0.],
[5., 0.]])
瞧!具有邻接矩阵,输入函数,权重和激活功能的完整隐藏层!
简单样例
最后,我们可以在真实图上应用图卷积网络。我将向你展示如何产生我们在文章开头看到的要素表示。
扎卡里的空手道俱乐部
扎卡里(Zachary)的空手道俱乐部是一种常用的社交网络,其中节点代表空手道俱乐部的成员,其边缘相互联系。当扎卡里(Zachary)研究空手道俱乐部时,管理者与教练之间发生了冲突,导致俱乐部分裂为两部分。下图显示了网络的图形表示,并且根据俱乐部的哪个部分标记了节点。管理员和讲师分别标有“ A”和“ I”。
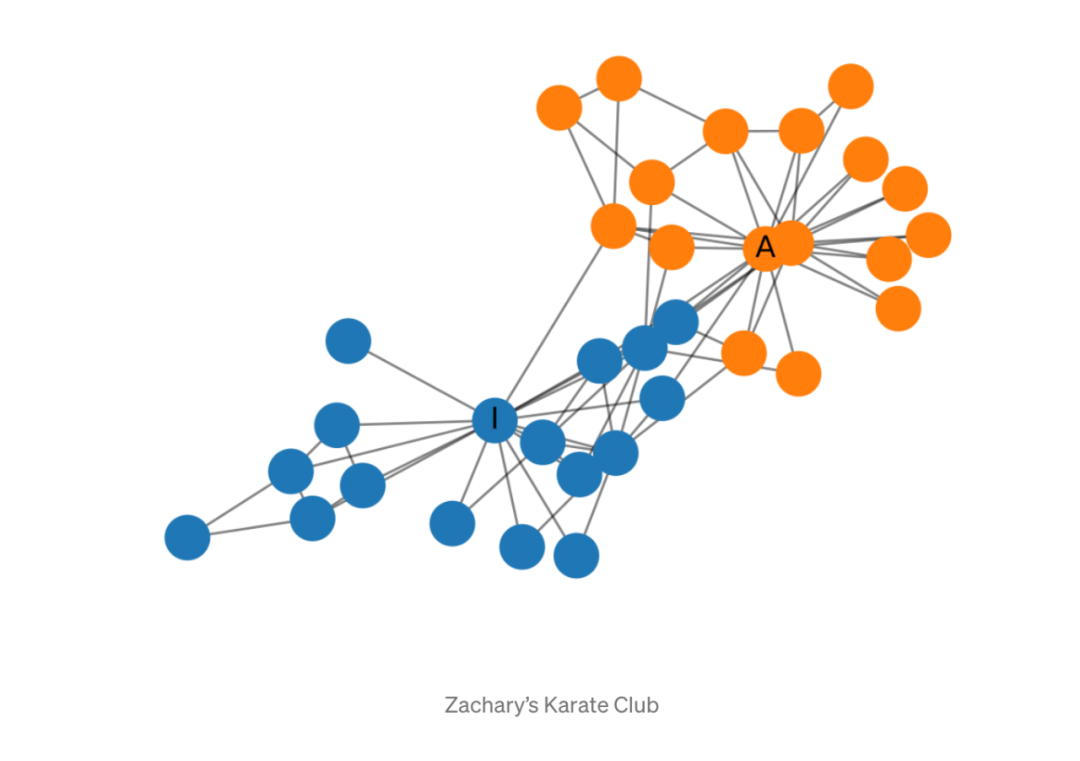
建立GCN
现在来建立图卷积网络。实际上我们不会训练网络,只是简单地随机初始化,以产生在本文开头看到的功能表示。我们将使用图网络networkx表示整个图,并计算A_hat和D_hat矩阵。
from networkx import karate_club_graph, to_numpy_matrixzkc = karate_club_graph()
order = sorted(list(zkc.nodes()))A = to_numpy_matrix(zkc, nodelist=order)
I = np.eye(zkc.number_of_nodes())A_hat = A + I
D_hat = np.array(np.sum(A_hat, axis=0))[0]
D_hat = np.matrix(np.diag(D_hat))
接下来,我们随机初始化权重。
W_1 = np.random.normal(
loc=0, scale=1, size=(zkc.number_of_nodes(), 4))
W_2 = np.random.normal(
loc=0, size=(W_1.shape[1], 2))
堆叠GCN层:在这里,我们仅使用单位矩阵作为特征表示,即,每个节点都表示为单次热编码的分类变量。
def gcn_layer(A_hat, D_hat, X, W):
return relu(D_hat**-1 * A_hat * X * W)H_1 = gcn_layer(A_hat, D_hat, I, W_1)
H_2 = gcn_layer(A_hat, D_hat, H_1, W_2)
output = H_2
提取特征表示:
feature_representations = {
node: np.array(output)[node]
for node in zkc.nodes()}
瞧!特征表示很好地将Zachary空手道俱乐部中的社区分隔开来。而且我们还没有开始训练!
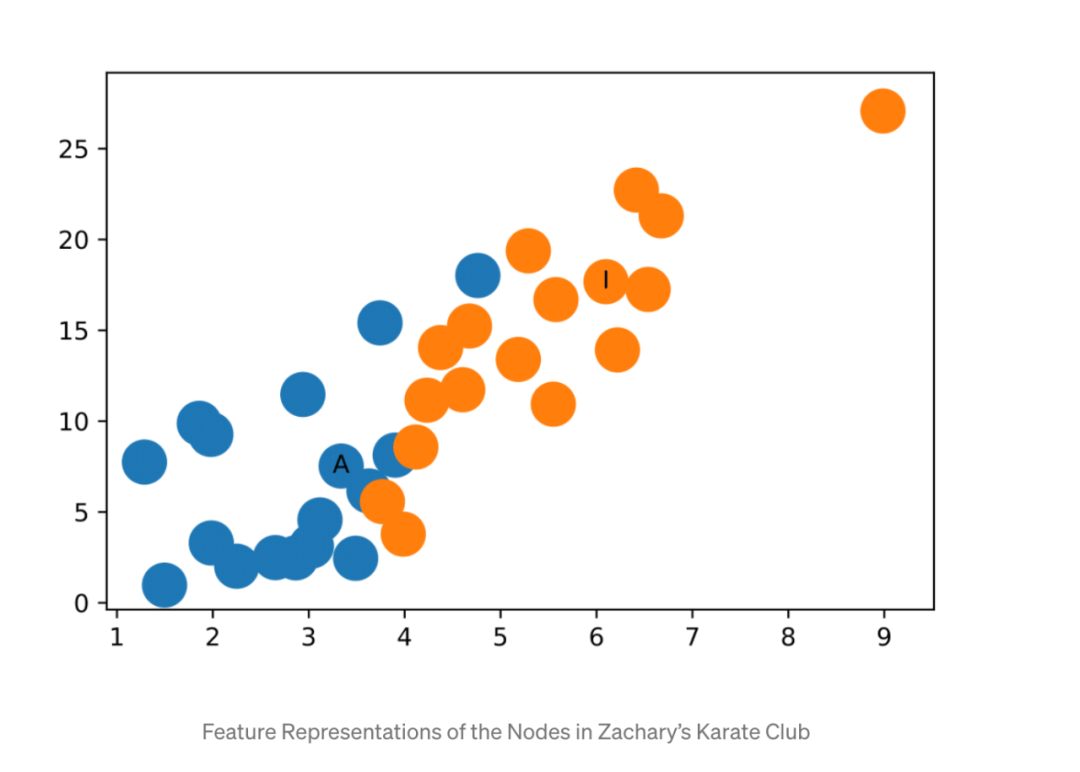
对于此示例,由于ReLU函数的作用,随机初始化的权重很有可能在x轴或y轴上给出0值,因此需要进行几次随机初始化才能产生上图。
结论
在这篇文章中,我对图卷积网络进行了高级介绍,并说明了GCN中每一层节点的特征表示是如何基于其邻域聚合而得出的。我们了解了如何使用numpy构建这些网络以及它们的强大功能:即使是随机初始化的GCN,也可以在Zachary的空手道俱乐部中分离社区。
「好了不能说太多了!剩下的GCN+新疆棉花事件就给给你了!你学废了么?🤔」

推 荐 阅 读
参 考 资 料
https://towardsdatascience.com/how-to-do-deep-learning-on-graphs-with-graph-convolutional-networks-62acf5b143d0
原创不易,有收获的话请帮忙点击分享、点赞、在看🙏
