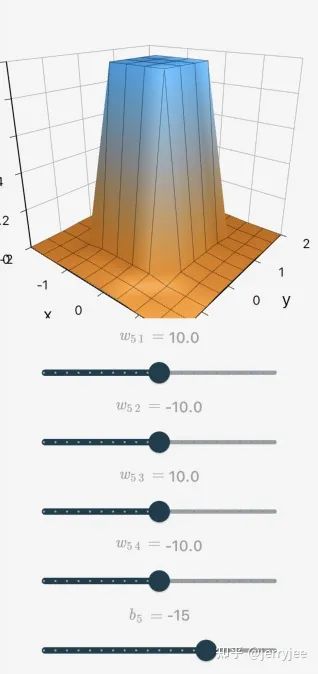
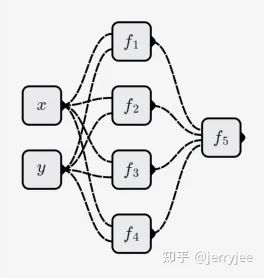
神经网络如何模拟任意函数?
机器学习算法与Python实战
共 1052字,需浏览 3分钟
·
2021-10-21 22:11
点击关注公众号,干货及时送达
地址:https://zhuanlan.zhihu.com/p/396204813
01
02
03
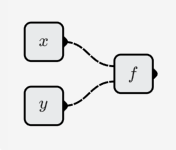
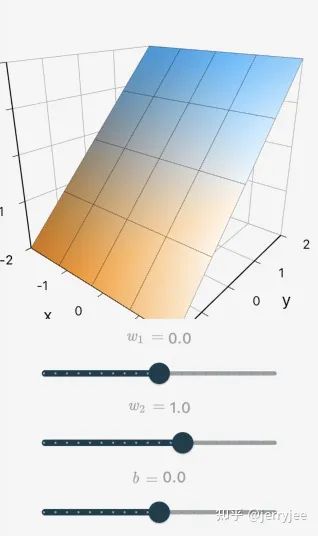
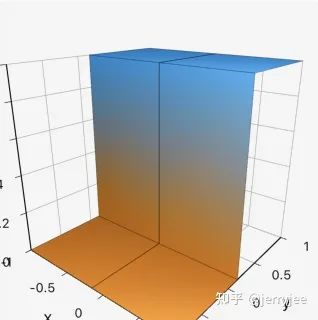
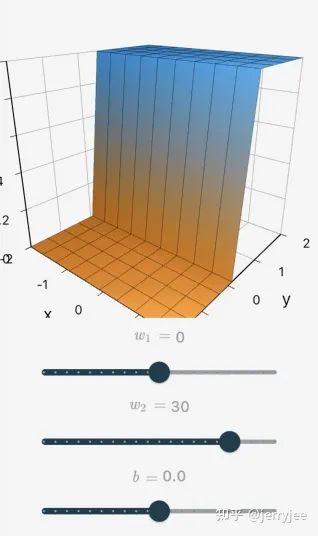
04
推荐阅读
(点击标题可跳转阅读)
老铁,三连支持一下,好吗?↓↓↓
评论

共 1052字,需浏览 3分钟
·
2021-10-21 22:11
点击关注公众号,干货及时送达
地址:https://zhuanlan.zhihu.com/p/396204813
01
02












03










04
推荐阅读
(点击标题可跳转阅读)
老铁,三连支持一下,好吗?↓↓↓