一致性哈希及其在Greenplum中的应用-轻识

点击上方蓝色字体，选择“设为星标”

回复”资源“获取更多资源

前言

一致性哈希(consistent hashing)是分布式系统中非常重要的算法，在平滑扩缩容、动态负载均衡等方向有大量应用。相对于传统的线性(取模)哈希算法，一致性哈希可以保证在分布式哈希表中的桶数量发生变化时，受到影响需要重新映射的key尽量少。本文先简要复习下经典的割环一致性哈希方案，然后介绍它的变种——跳跃一致性哈希(jump consistent hash)。

割环一致性哈希

一致性哈希的概念最初在1997年由David Karger等大佬提出，原始论文见Consistent Hashing and Random Trees: Distributed Caching Protocols for Relieving Hot Spots on the World Wide Web，起初是为了解决网络中的热点问题，后来发展成分布式系统中通用的算法。为了与此后出现的其他一致性哈希算法相区别，一般将这个经典方法称为“割环法”。该算法能够满足论文中提出的两大目标，即平衡性(balance)和单调性(monotonicity)。

顾名思义，割环法将整个哈希空间组织成一个首尾相接的圆环，一般设为[0, 232 - 1]。以分布式K-V存储为例，哈希桶即为存储节点。将节点N的编号或IP等按哈希函数hash(N)映射在环上，再将数据的key按同样的哈希函数hash(k)映射在环上，数据就会存储在环上以顺时针方向遍历找到的第一个节点。当节点扩容或缩容时，仍然按照顺时针原则，将受到影响的区间内的数据重新分布到相邻的节点上去，达到增量更新的目的，即满足单调性。以下3张图能够简单地说明。

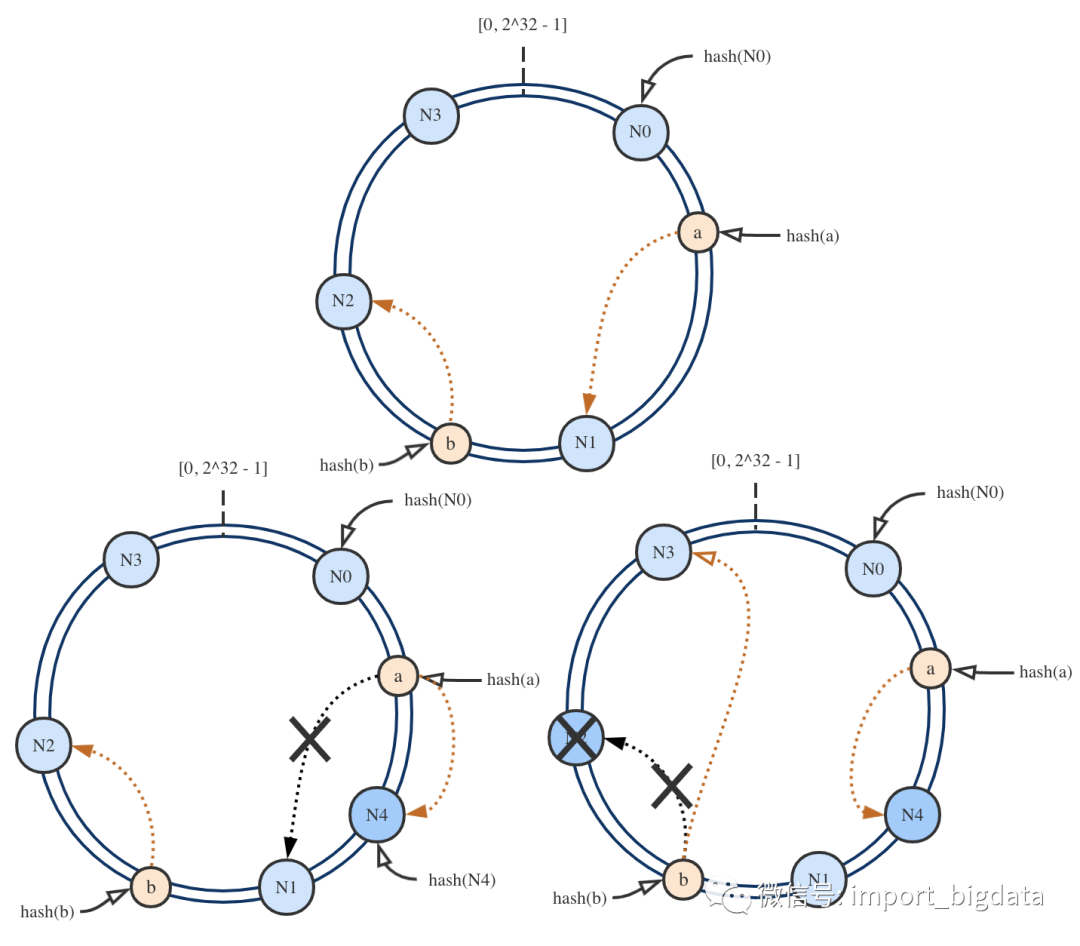
虽然哈希函数的结果是均匀的，但节点映射在环上可能不均匀，节点数越少，数据倾斜的可能性就越大。解决此问题的方法是将物理节点虚拟成多个影子节点，数据经过哈希后按顺时针原则落到影子节点指向的物理节点上。如果我们想要人为干预各节点上数据量的权重，还可以指定不同的影子节点数量。如下图所示，影子节点数量为3:2:2:1。

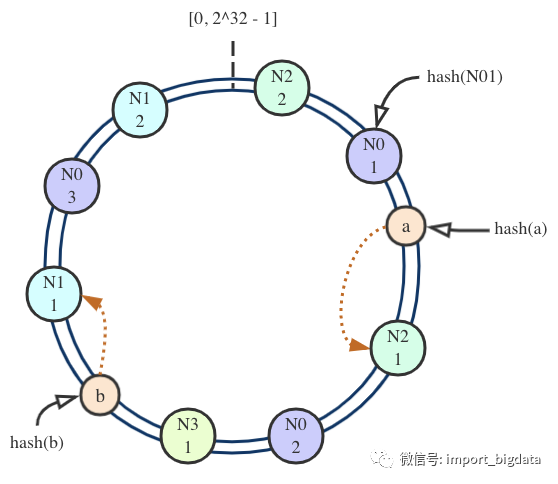
虚拟节点扩缩容时的数据迁移方法与仅采用物理节点相同，因此调整权重值也会触发数据迁移。

对于有N个桶和K个键的一致性哈希方案，其时间复杂度是：

添加、删除节点——O(K / N + logN)；
添加、删除key——O(logN)。

其中，O(K / N)是数据重分布操作的平均代价，O(log N)则是在环上进行二分查找定位哈希桶的代价。

最后有一个小问题：节点扩缩容以及节点宕机时如何保证系统仍然可用呢？有两种直接的思路：

中继——如果在某个节点上查不到所需的数据，就把请求转发给该节点的顺时针方向下一个节点进行处理。
双写——每次写入数据时，都另外写一份到目标节点的顺时针方向下一个节点。

割环法已经能够满足一般分布式系统中的多数需求，Cassandra、Memcached等著名的存储系统都用到了它(注意Redis Cluster并没有)。下面介绍思想更加精妙，效率也更高的跳跃一致性哈希(jump consistent hash)方法。

跳跃一致性哈希

这个算法比较年轻，在2014年由Google的大佬John Lamping和Eric Veach提出，原始论文见A Fast, Minimal Memory, Consistent Hash Algorithm。它的实现非常简洁，仅有5行代码，如下。

int32_t JumpConsistentHash(uint64_t key, int32_t num_buckets) {
  int64_t b = 1, j = 0;
  while (j < num_buckets) {
    b = j;
    key = key * 2862933555777941757ULL + 1;
    j = (b + 1) * (double(1LL << 31) / double((key >> 33) + 1));
  }
  return b;
}

看官可能还无法理解为什么能这样实现，接下来重走一遍论文的推导思路。

假设最终要求的满足平衡性和单调性的哈希函数是ch(k, n)(k为数据的键，n为哈希桶的数量)，有如下简单的递推关系：

当n = 1时，所有key都要映射到同一个桶中，即ch(k, 1) = 0；
当n = 2时，为保证均匀性，需有K / 2个key分别映射到两个桶中(K是key的总数量)，故K / 2个key需要重新映射；
......
当桶数量由n变为n + 1时，有K / (n + 1)个key需要重新映射。

那么该如何决定哪些key被重新映射到新的桶中呢？答案是采用线性同余法(LCG)生成的伪随机数决定。上文中的magic number 2862933555777941757就是线性同余法的乘数a。

以k作为种子生成一个伪随机数序列，可以保证对于确定的k，ch(k, n)的结果也是确定的，进而使用条件rand < 1 / (j + 1)即可保证哈希桶由j个变为j + 1个时，有1 / (j + 1)比例的数据会重新映射。

此时ch()函数的逻辑如下，时间复杂度显然为O(n)。

int ch(int key, int num_buckets) {
  random.seed(key);
  int b = 0; // This will track ch(key, j+1).
  for (int j = 1; j < num_buckets; j++) {
    if (random.next() < 1.0 / (j + 1)) b = j;
  }
  return b;
}

这个复杂度比割环法还要高，如何优化？容易想到，rand < 1 / (j + 1)的概率肯定是相对小的，也就是说随着j的增大，发生重分布的key的比例越来越小，j可以不必逐次自增，而是跳跃前进，这也就是算法名称中"jump"一词的由来。

观察上面的代码，b表示k最后一跳的目的哈希桶的编号，即满足条件：

ch(k, b + 1) ≠ ch(k, b) && ch(k, b + 1) = b

假设k连续不跳变，直到增加到j + 1个桶才发生跳变，可知此概率为：

[(b + 1)/(b + 2)] * [(b + 2)/(b + 3)] * ... * [(j - 1)/j] = (b + 1) / j

或者表示为：

P[j ≥ i] = P[ch(k, i) = ch(k, b + 1)] = (b + 1) / i

图示如下。

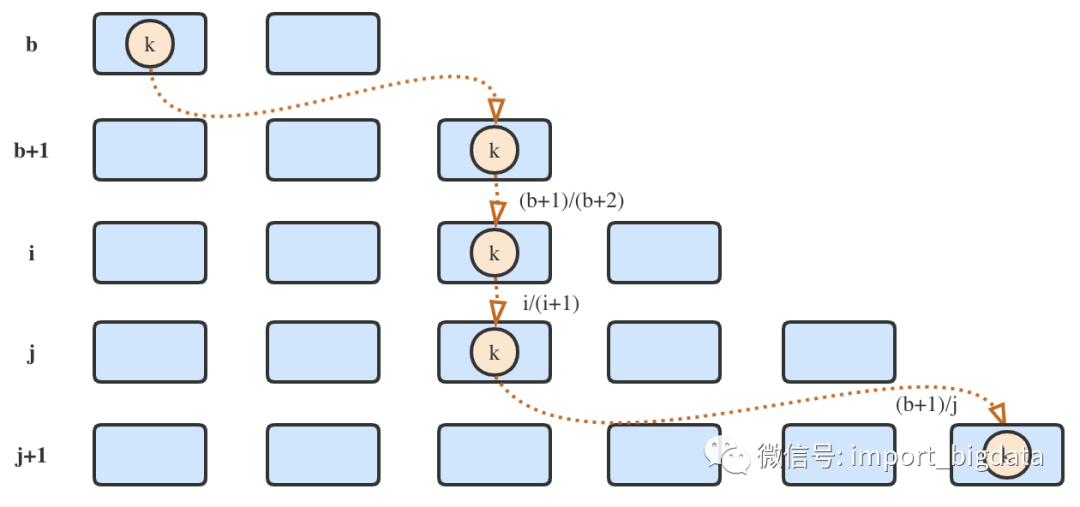
那么，j最多可以直接跳到哪里才不至于漏掉原有的循环过程呢？容易得知，要满足rand < (b + 1) / j，需要j < (b + 1) / rand，将其向下取整即可。改进后的ch()函数如下。

int ch(int k, int n) {
  random.seed(k);
  int b = -1, j = 0;
  while (j < n) {
    b = j;
    r = random.next();
    j = floor((b+1) / r);
  }
  return b;
}

将random替换为具体的LCG，就是本节开头的算法了。

分析时间复杂度：对于任意一个k，在哈希桶数从1增加到n的过程中，发生跳跃的期望次数是1 / 2 + ... + 1 / i + ... + 1 / n。根据欧拉常数的定义，调和级数与自然对数的差值的极限会收敛到一个小数，因此跳跃一致性哈希算法的复杂度是O(ln n)，比割环法更优。

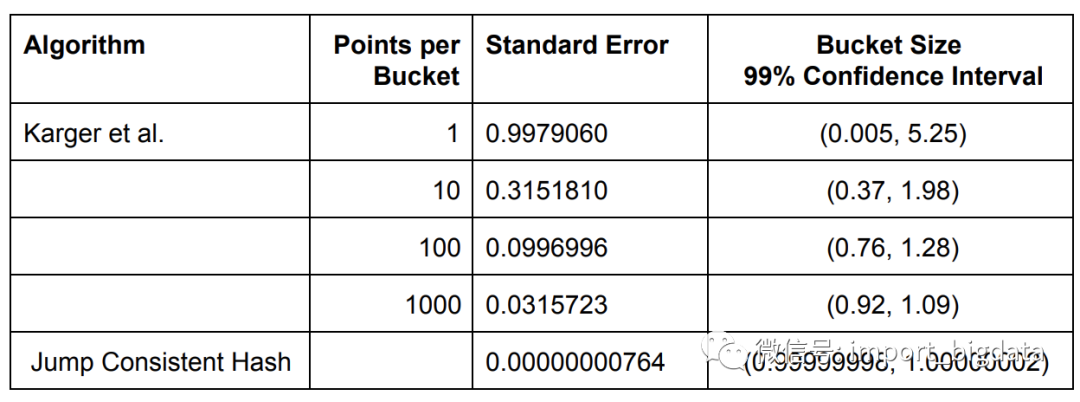
根据论文给出的实验数据，跳跃一致性哈希产生的分布的标准差远远比割环法小，也就是非常均匀。

随着桶数量的增加，跳跃一致性哈希算法的执行时间增长也不明显。

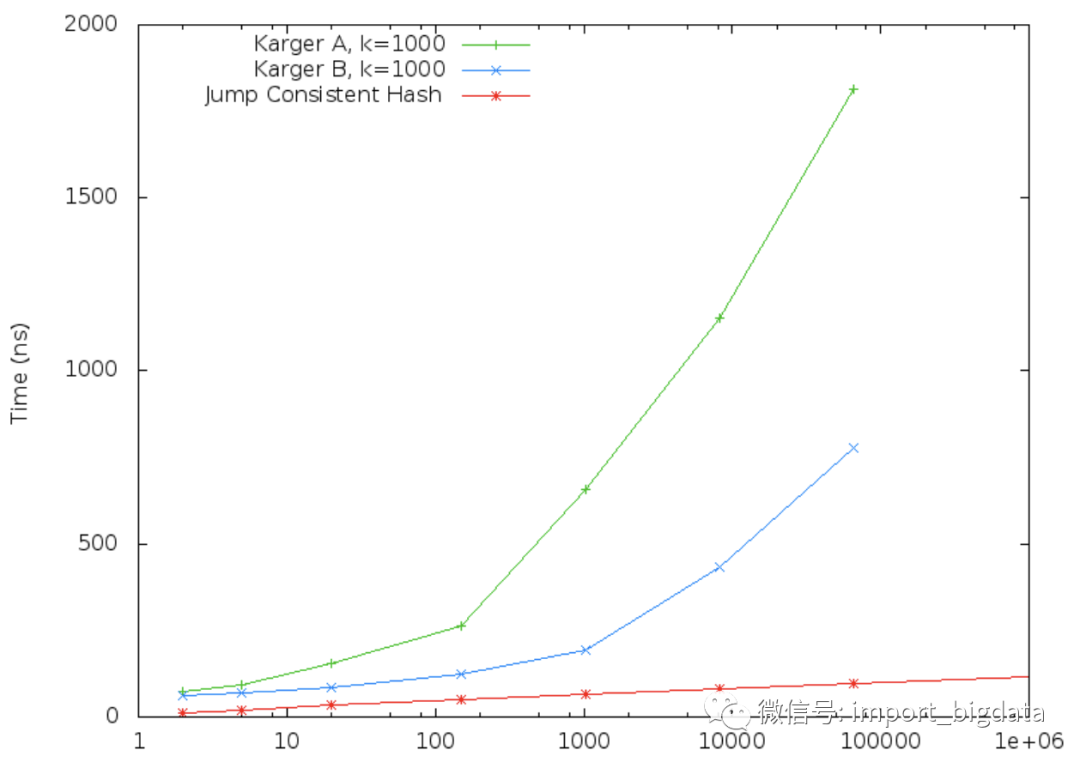
另外，它不需要额外的数据结构，内存占用极小(即论文标题中所说的minimal memory)。

但是，它相对于割环法而言有个非常大的缺点，即只能在哈希桶序列的尾部添加和删除桶，而不能在中间增删。显而易见，如果在中间增删桶，由于桶的标号是按自然顺序来的，因此会导致后方所有桶的标号发生变化，不再满足一致性哈希的基本性质。

仍然考虑节点扩缩容以及节点宕机时如何保证系统仍然可用的问题。

中继——如果在尾部的哈希桶j + 1中查不到所需的数据，就把请求转发给ch(k, j)桶，即它的上一跳节点。
双写——每次写入数据时，如果写入的是尾部的哈希桶j + 1，就另外写一份到ch(k, j)；如果写入的是非尾部的哈希桶i，就另外写一份到i + 1。这样，不管是哪个节点失败，数据都不会丢失。

Greenplum中的应用

Greenplum提供了一个为集群扩容的工具gpexpand。在GP v5中，执行gpexpand时需要将所有哈希分布改为随机分布，按照新的集群规模重新根据hash key计算哈希值，再将数据重新均衡到各个segment节点上，相当于进行了一次完全的shuffle，如下图所示。

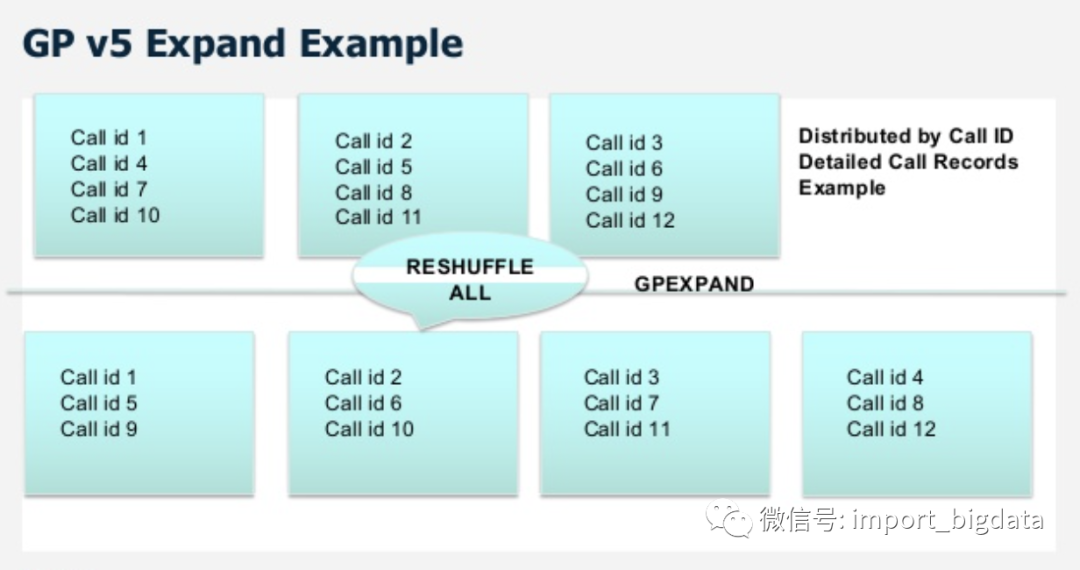
这种方式的缺点显而易见：集群在扩容期间处于不可用状态，数据交换量巨大。并且在数据由随机分布转为新的哈希分布之前，无法利用数据的本地性信息做查询优化，拖累性能。

在GP v6中，通过将跳跃一致性哈希引入gpexpand，实现了完全在线、高性能的集群扩容方式。如下图所示，将集群由3节点扩容到4节点，只有1/4的数据需要重分布。

GP v6的跳跃一致性哈希实现与Google原版完全相同。

另外，如何保证那些没有重分布完毕的表被正确地查询呢？GP v6在catalog表gp_distribution_policy里加入了一个新的字段numsegments，表示一张表的数据分布在前numsegments个节点上。因此，就算扩容的过程中有事务正在运行，只要numsegments没有改变，就仍然只在原有节点上执行查询。

最后，可以通过全局配置gp_use_legacy_hashops设定是否改回旧版的取模哈希方式，默认当然为false。

一万五千字详解HTTP协议

Spark如何协调来完成整个Job的运行详解

最新Hive/Hadoop高频面试点小集合

欢迎点赞+收藏+转发朋友圈素质三连

文章不错？点个【在看】吧！