盲去卷积 - 更加实用的图像去模糊方法 Wang Hawk

上一篇文章35. 去卷积:怎么把模糊的图像变清晰?吸引了很多朋友的关注。在这篇文章里面,我给大家讲了一种叫做“非盲去卷积”的方法,当指定了PSF(下图中的c),和观测到的模糊图像(下图中的b),我们可以恢复出清晰的图像(下图中的x)。

很多人都觉得去卷积大法好啊,真的可以把渣画质变清晰。可就是需要提前知道PSF,这可就难了。确实,很多情况下提前测定PSF是根本不可能的,有可能你手上只拿到了一张很模糊的照片b,不知道c,想要恢复出x,这时候应该怎么办呢?

事实上,这也是可以办到的,这就是所谓的“盲去卷积”(Blind Deconvolution),今天我就给大家介绍这种技术。
我们先来看两组盲去卷积的结果,给大家一些直观的感受:


上面的结果来自于盲去卷积领域非常经典而基础的文章:
Fergus et al., “Removing camera shake from a single image,” SIGGRAPH 2006.
今天我主要就为你介绍这篇文章的思想
一、盲去卷积的基本思想
1.1 利用先验信息
小明是第一次用单反的摄影小白,他刚刚很兴奋的端起相机拍了一张照片:
Oops!手没拿稳,拍出了一张超模糊的照片:

我们看看小明的相机在拍照瞬间的运动轨迹

很显然,他这样是拍不出来好片子的,我们来简化一下他这张照片的生成过程:

上图中的模糊核(PSF)是由于小明端起相机时的随机抖动导致的,我们无法提前测定,那么怎么样才能把清晰图像恢复出来呢?这真是一个超难的问题。
这就像你知道了11这个数是由2个数的乘积构成的,要让你猜出是哪两个数一样困难:
一张模糊的图像,也有可能有多种生成模式,只有最下面这种才是我们需要的,怎么才能得到它呢?

很显然,我们需要利用一些先验信息。有两个关键的先验信息可以帮助我们
1 - 图像的梯度分布
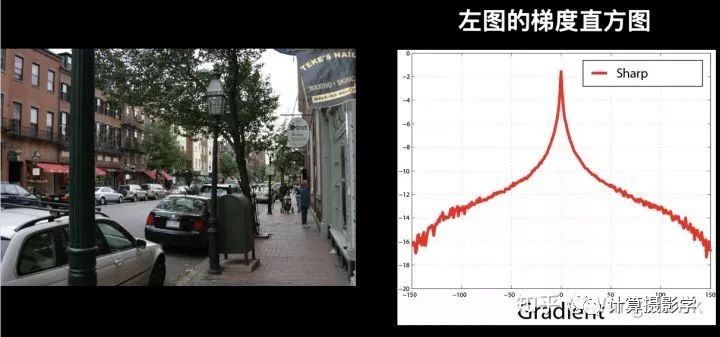
清晰的自然图像的梯度符合一种叫做"Heavy-Tail"的分布形态。直观上讲,一张清晰图像里面有很多平滑的区域且噪声较低,所以梯度接近0的像素还是占大多数。但是由于图像清晰,所以物体的边界比较明显,所以还是有很多像素的梯度较大。因此这种梯度的分布大概长这个样子(梯度直方图的纵坐标是Log化的密度):
但是模糊的图像的边缘被糊掉了,所以更多的像素的梯度趋于0,因此其梯度直方图就会变化:
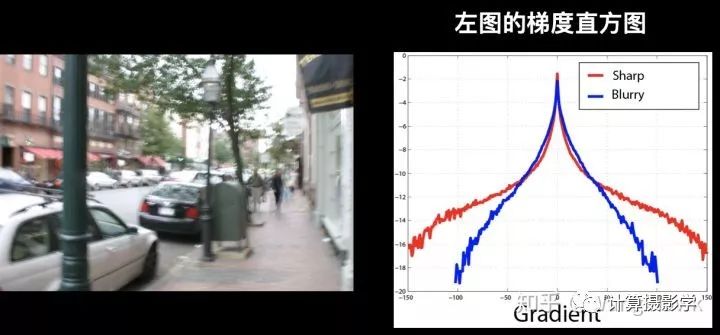
所以我们想要寻找的是符合上面重尾分布的图像,而不是其他随随便便的图像
2 - 模糊核的形态
我们这里展示的是相机的运动导致的模糊,那么可以认为模糊核是稀疏的,有连续的轨迹,并且模糊核值都是非负数。所以我们重建出来的模糊核也不是随随便便的,它必须符合上述这些特点才是一个合格的运动模糊核。
3 - 噪声
相机总是有噪声的,为了简化问题,我们可以假设噪声是均值为0的高斯噪声
于是,我们就有了几种信息用于重建清晰的图像
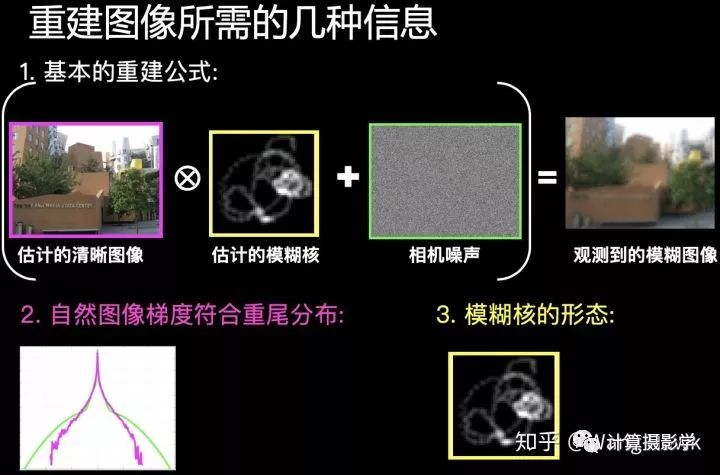
1.2 问题的数学建模
已知模糊图像P,未知图像为L,未知的卷积核为K。一个基本的想法是把问题看做是求最大后验概率的问题:
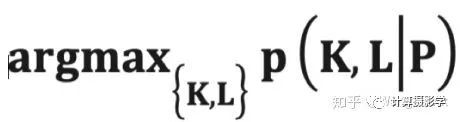
其中K和L满足一定的先验条件的约束。我们所需的就是把后验概率公式表达出来。为了让这篇文章能够比较容易看懂,我把相关的细节列到文章的后面,这样你可以更连贯的阅读这篇文章。
1.3 问题的求解
作者尝试了用标准的MAP求解方法来求解出K和L,但最终效果却很差

作者对此的解释是MAP目标函数会尝试让所有像素的梯度都最小化,而实际的自然图像中包含有大量高梯度的区域。
而在2009年的下面这篇著名论文中,作者Levin教授则提出了更深入的见解。
Levin et al., “Understanding and evaluating blind deconvolution algorithms,” CVPR 2009 and PAMI 2011
Levin教授认为用MAP目标函数同时求解K和L肯定不好,有如下的原因:
错误的单位卷积核比起正确的稀疏卷积核的可能性更高(Levin的论文中有证明)

2. 上述MAP目标函数的变量个数具有高度的非对称性,比如对于这幅毕加索照片:

可见已知量的个数总是小于未知量的个数 #P < #L + #K
以上两个原因就会导致用这种同时估计K和L的目标函数来做MAP总是无法得到好的结果。那有没有更好的方法呢?
Levin认为,更好的办法是只单独估计K,即把下面左边的问题转换为右边的问题
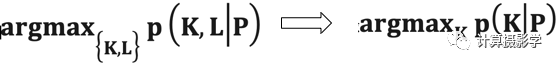
这样,已知量的个数就远远大于未知量的个数 #P >> #K
这里的p(K|P)是相对于L的边际概率,即:
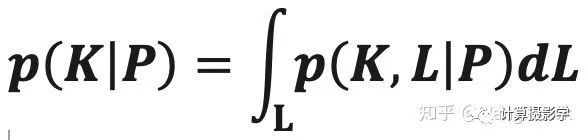
简单来说,就是对每一个可能的K,我们都要在所有可能的L上求取其后验概率,并把这些后验概率值加起来,得到p(K|P)。你应该可以感觉到求这样的边际概率也是很不容易的事情,计算量非常复杂。于是很多学者采用了近似的方式来进行求解。回到我们开头介绍的Fergus的论文,作者是采用了“变分贝叶斯(variational Bayesian)”方法来近似后验概率的表示和求取
Fergus证明了这种方法能得到远比原始的同时求取K和L的MAP算法好。

二、完整的流程
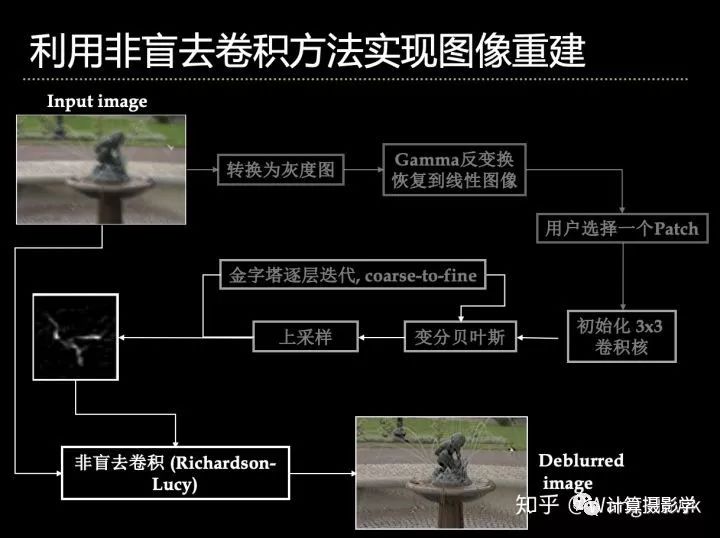
在论文中, Fergus展示了其完整的盲去卷积的流程:
第一步:预处理图像,为了降低计算量,并得到良好的结果,需要用户来选择一个图像块。
第二步:利用变分贝叶斯,估计卷积核K。为了避免陷入局部最优,作者采用了coarse-to-fine的策略
第三步:利用标准的非盲去卷积方法,重建清晰图像L。作者采用了我在上一篇文章里面提到的Richardson-Lucy算法进行。




三、效果展示



四、后验概率的细节
正如前面所讲,为了求解问题,需要把后验概率用公式表达出来。先引入一些符号来说明问题:
 :模糊图像块
:模糊图像块 :可能的模糊核
:可能的模糊核 :可能的清晰图像块
:可能的清晰图像块 : P的梯度
: P的梯度 : Lp的梯度
: Lp的梯度 :噪声
:噪声
首先,我们前面讲过

由于卷积运算是线性运算,因此可以有:

这样我们可以把后验概率改写为

用MAP的思想来说,问题就转换为求使得上述概率最大的K和 
我们可以用贝叶斯公式将这个后验概率展开:
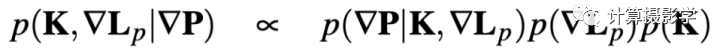
我们分别来看后面三项:
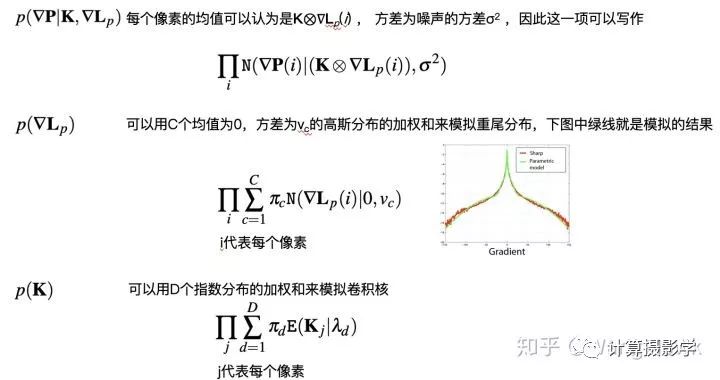
于是上面的后验概率就可表示为:
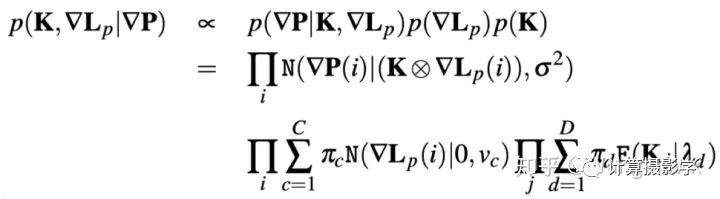
五、算法值得改进的地方
在文章中Fergus提到的几个点都是值得改进的:
假设噪声满足高斯分布
用混合高斯模型来拟合重尾模型
用混合指数分布来描述模糊核的形态
多尺度的变分贝叶斯算法复杂度较高,需要用户的手动引导选择小的图像块
采用的非盲去卷积是RL算法,相信会有更好的方法来改善图像质量
等等
作者本身也在其文章中提到了一些值得改进的地方,能让后人在此基础上对 这项工作有所完。果不其然,在随后几年的CVPR, SIGGRAPH, ICCV, ECCV上, 几乎每届都有更好的结果涌现。
比如下面这篇2008年Jiaya Jia团队的文章就作出了非常好的效果:
Shan et al., “High-quality Motion Deblurring from a Single Image,” SIGGRAPH 2008
文章的改善点包括了:
更复杂的噪声模型,噪声的概率分布由其0阶、1阶、2阶梯度的分布来描述
更简单的拟合重尾分布的函数
加入了局部平滑区域的约束,避免出现振铃效应
复杂的优化方法,交替式的优化估计清晰图像L和模糊核K
下面是算法的效果,还是非常不错的:

这个领域后面出了非常多效果更好的文章,在github上有一个专门的项目整理记录:
六、总结
去卷积分为非盲去卷积和盲去卷积,我介绍的用途主要是图像的去模糊。今天介绍的Fergus的文章利用了变分贝叶斯算法来求解模糊核K,然后利用经典的非盲去卷积算法Richardson-Lucy算法来进行清晰图像的恢复。从今天介绍的文章你可以看到,理解盲去卷积的算法对图像的统计信息、概率知识、最优化求解方法的要求要比非盲去卷积高很多。坦率说,我自己在看这些文章时也感觉很吃力。
但我希望这篇文章能给你打开一扇大门,让你可以透过它看到一片新的研究天地。如果你喜欢这篇文章,请给我点赞,谢谢!😃
好消息!
小白学视觉知识星球
开始面向外开放啦👇👇👇
下载1:OpenCV-Contrib扩展模块中文版教程 在「小白学视觉」公众号后台回复:扩展模块中文教程,即可下载全网第一份OpenCV扩展模块教程中文版,涵盖扩展模块安装、SFM算法、立体视觉、目标跟踪、生物视觉、超分辨率处理等二十多章内容。 下载2:Python视觉实战项目52讲 在「小白学视觉」公众号后台回复:Python视觉实战项目,即可下载包括图像分割、口罩检测、车道线检测、车辆计数、添加眼线、车牌识别、字符识别、情绪检测、文本内容提取、面部识别等31个视觉实战项目,助力快速学校计算机视觉。 下载3:OpenCV实战项目20讲 在「小白学视觉」公众号后台回复:OpenCV实战项目20讲,即可下载含有20个基于OpenCV实现20个实战项目,实现OpenCV学习进阶。 交流群
欢迎加入公众号读者群一起和同行交流,目前有SLAM、三维视觉、传感器、自动驾驶、计算摄影、检测、分割、识别、医学影像、GAN、算法竞赛等微信群(以后会逐渐细分),请扫描下面微信号加群,备注:”昵称+学校/公司+研究方向“,例如:”张三 + 上海交大 + 视觉SLAM“。请按照格式备注,否则不予通过。添加成功后会根据研究方向邀请进入相关微信群。请勿在群内发送广告,否则会请出群,谢谢理解~
