3D 游戏开发入门必备:3D 数学基础之坐标系
对于想要入门 3D 游戏开发的开发者来说,掌握一些基本的 3D 数学概念是必不可少的。Cocos Star Writer 白玉无冰最近重读了《3D数学基础:图形与游戏开发》一书,并整理了清晰且详实的读书笔记,相信能给正在学习 3D 的开发者们带去启发。
白玉无冰决定开一个新坑,再次重读《3D数学基础:图形与游戏开发》(第一版),同时结合 Cocos Creator 引擎及其他相关书籍,整理并记录一些笔记。

第一章,我们从坐标系开始看起。
坐标系有许多种,本文主要围绕笛卡尔坐标系(Cartesian Coordinate System)展开。
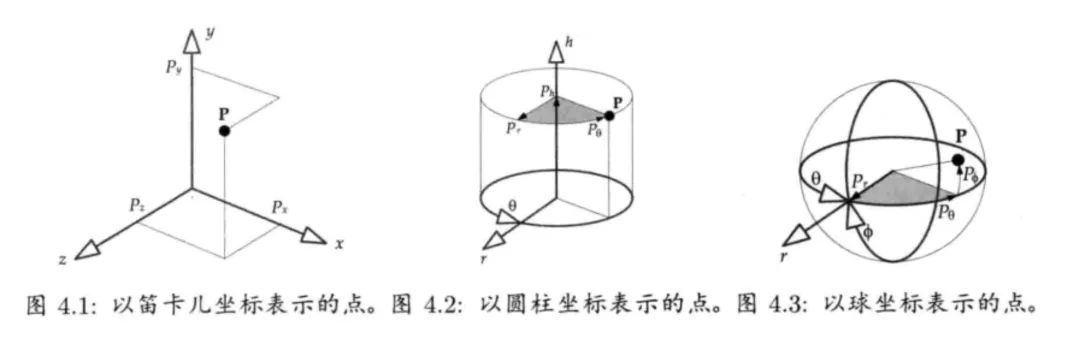
摘自《游戏引擎结构》
计算机图形学第一准则:近似原则。如果它看上去是对的,它就是对的。
左手坐标系与右手坐标系
3D 坐标系中存在两种坐标系:左手坐标系和右手坐标系。
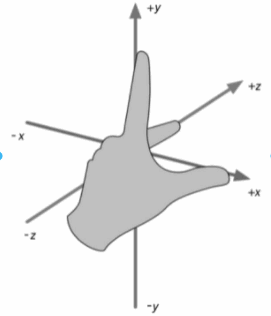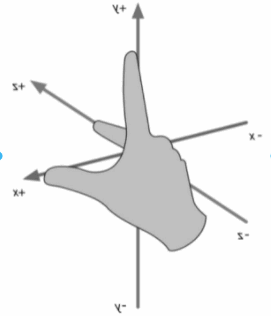
伸出你的双手,让拇指(x)、食指(y)和中指(z)相互垂直,就构成了相应的坐标系。
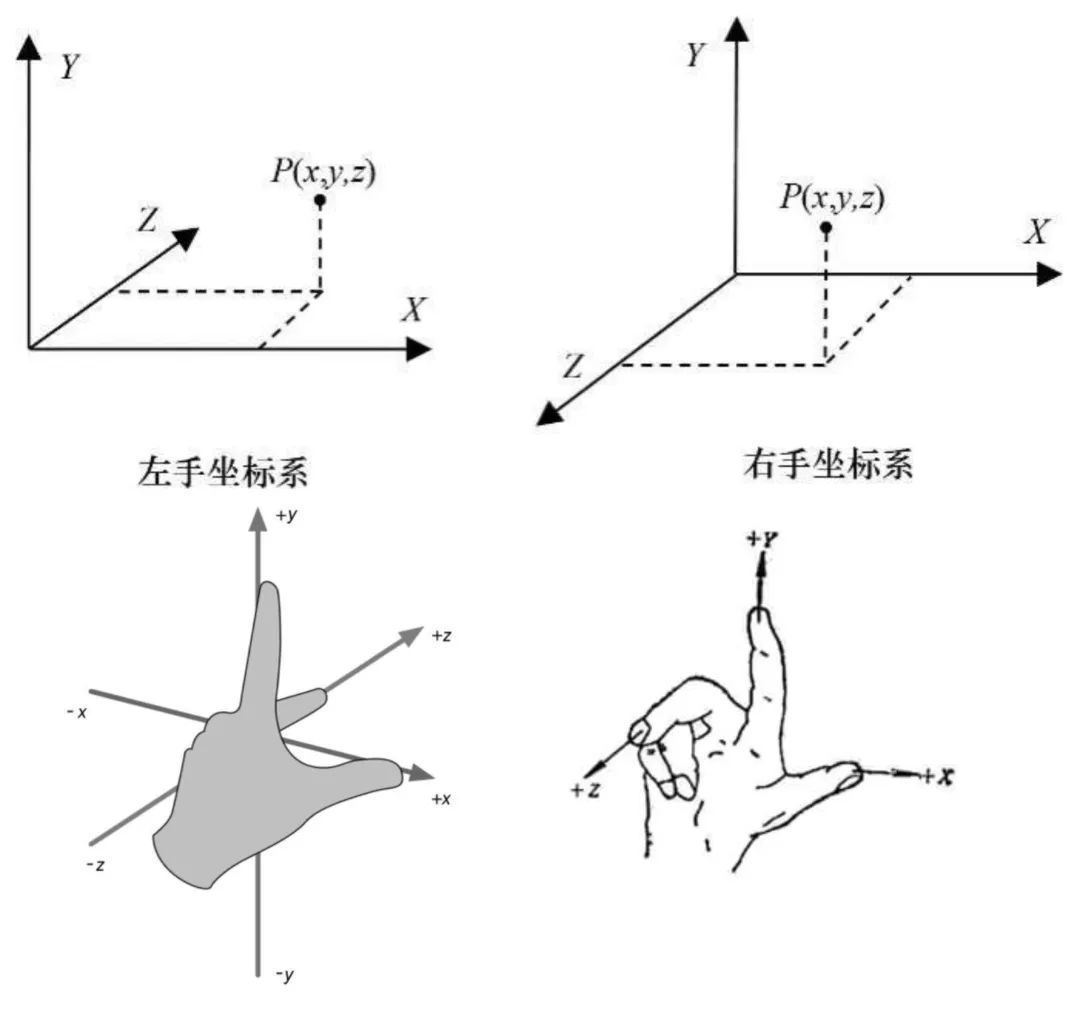
左手坐标系与右手坐标系
OpenGL 中的坐标系大体是右手坐标系,而 Direct3D 中大体是左手坐标系。
🥥 Cocos Creator 3.0 的世界坐标系采用的是笛卡尔右手坐标系,默认 x 向右,y 向上,z 向外,同时使用 -z 轴为正前方朝向。
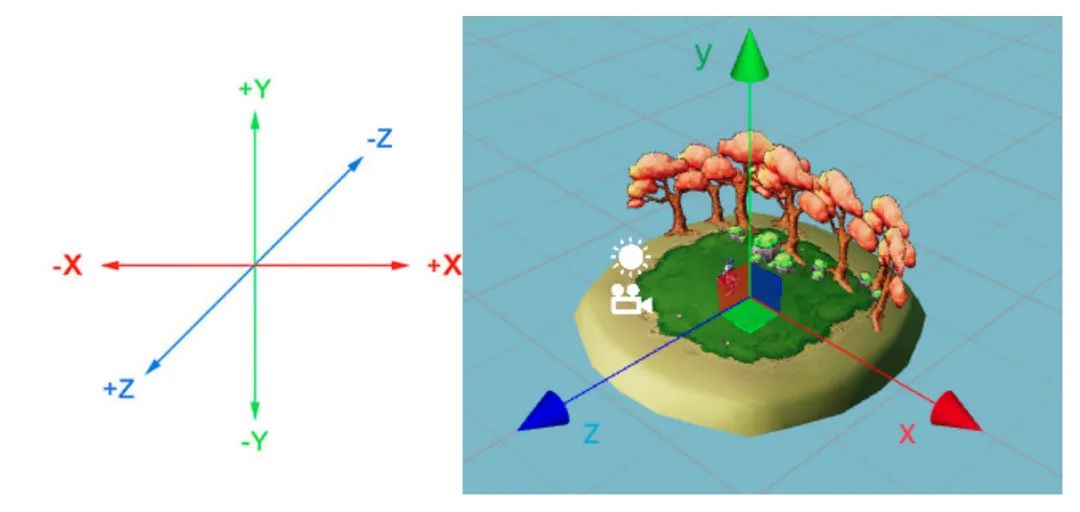
Cocos Creator 与右手坐标系
其中旋转也遵循对应左右手法则,伸出双手,做一个「点赞」 的手势,拇指指向朝向,四指握着的方向为正。
的手势,拇指指向朝向,四指握着的方向为正。
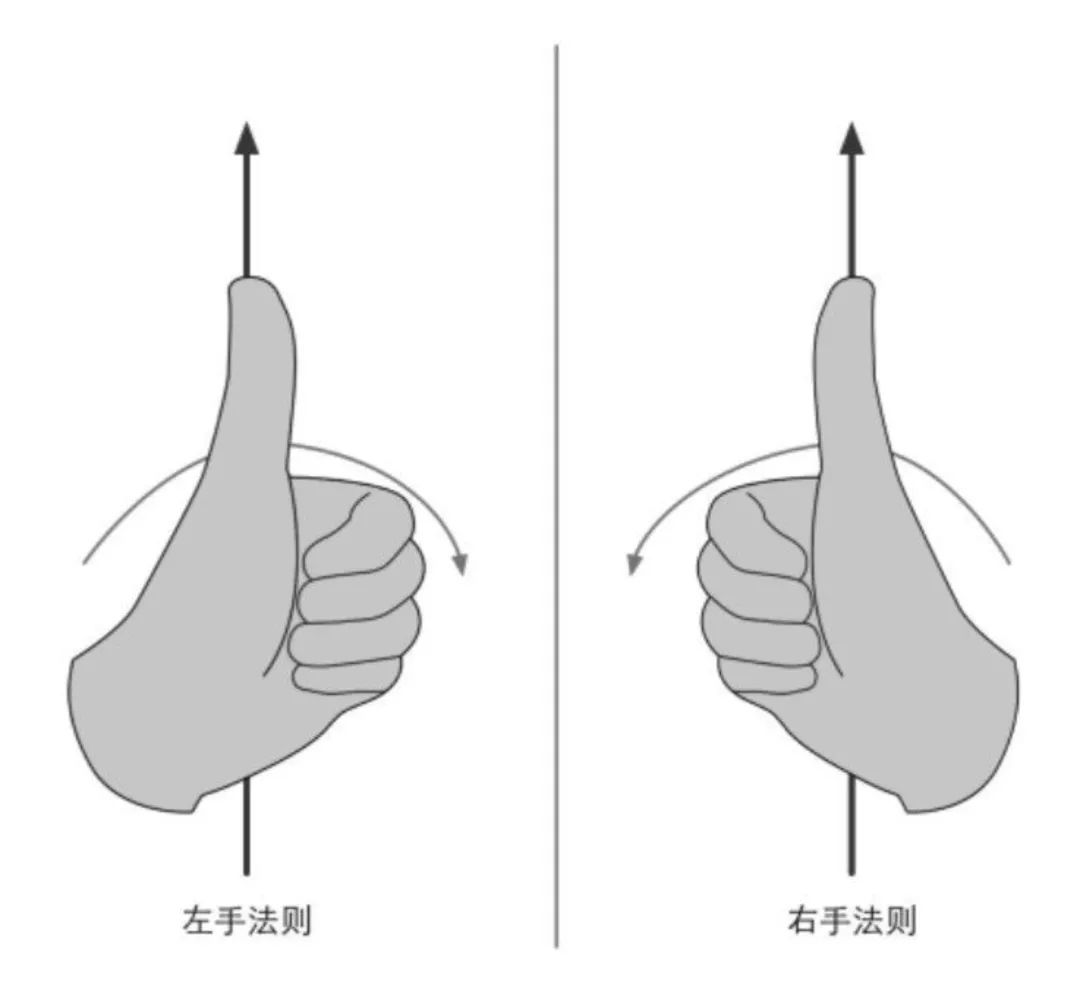
旋转与左右手
🥥 Cocos Creator 3.0 中的旋转(Rotation)遵守右手法则,从转向轴往原点看,当属性值为正时,节点逆时针旋转;当属性值为负时,节点顺时针旋转。
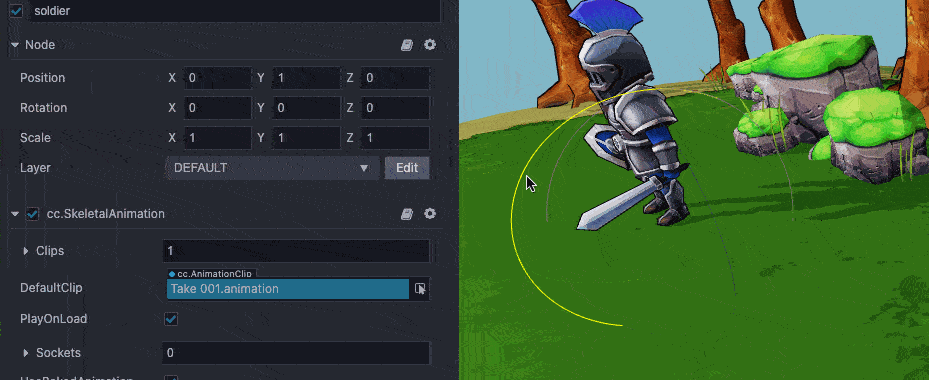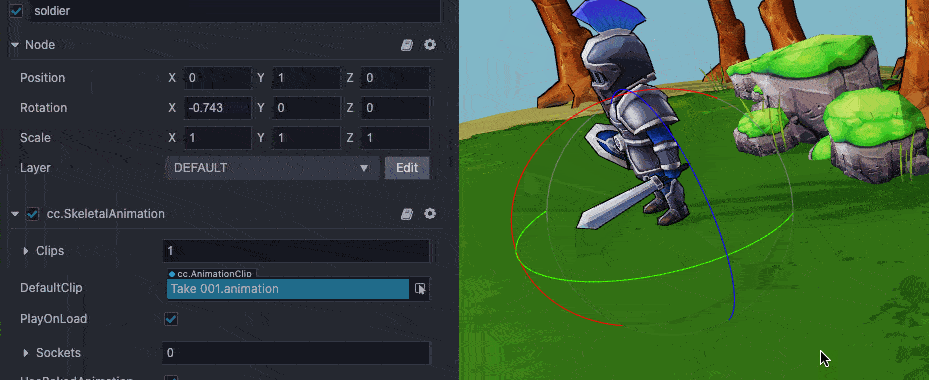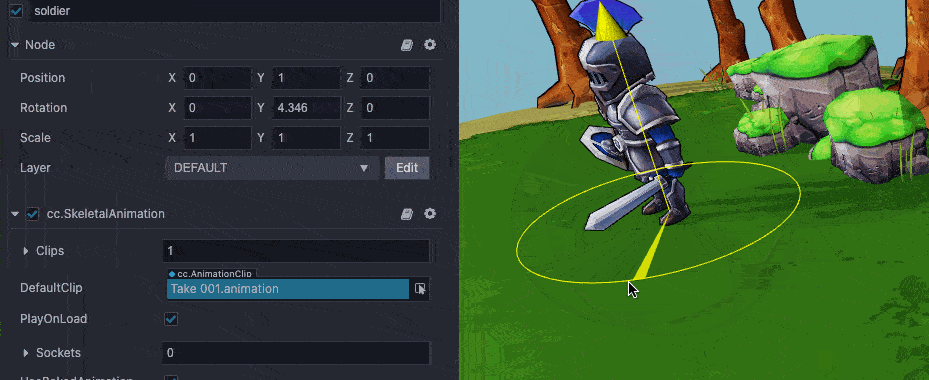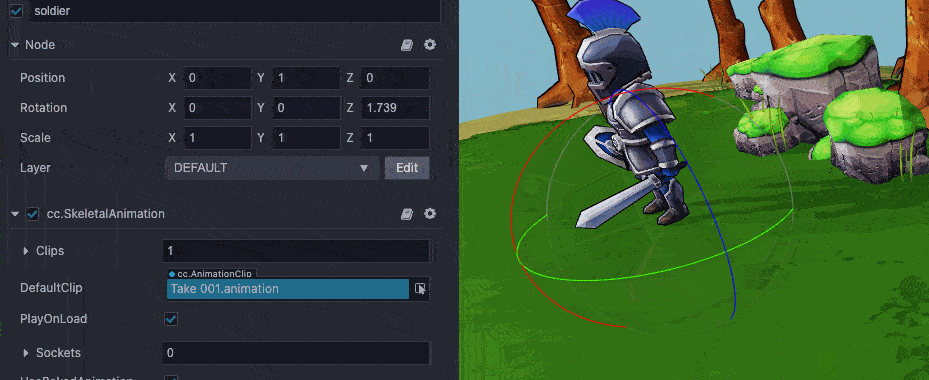
Cocos Creator 旋转
注意:节点上的 rotation 属性是一个四元数,表示的是绕任意轴旋转的角度。与属性检查器中的 Rotation 所对应的属性是欧拉角属性 EulerAngles。这两个属性可以根据需求分别使用,在使用 API 时请一定要注意它们和编辑器面板属性名的对应区别。
左右手坐标系可以相互转换,只需翻转一个轴的符号。
翻转一个轴
世界坐标系
世界坐标系(World Coordinate)是一个特殊的坐标系,它建立了我们所关心的最大的空间。世界坐标系也被广泛称作全局坐标系或者宇宙坐标系。
世界坐标系建立了描述其他坐标系所需要的参考框架。也就是说,能够用世界坐标系描述其他坐标系的位置,而不能用更大的、外部的坐标系来描述世界坐标系。
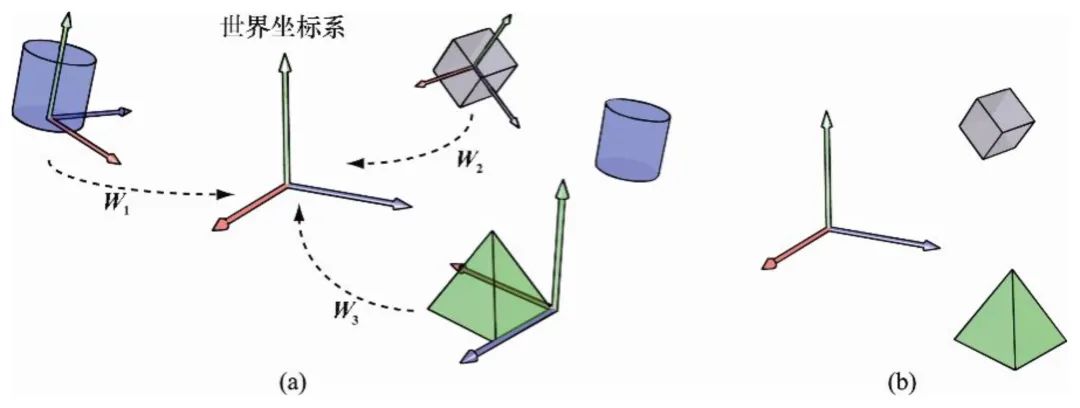
世界坐标系
关于世界坐标系的典型问题都是关于初始位置和环境:
每个物体的位置和方向
摄像机的位置和方向
世界中每一个点的地形是什么
各个物体从哪里来,到哪里去(NPC运动策略)
🥥 世界坐标系也叫做绝对坐标系,在 Cocos Creator 3.0 游戏开发中表示场景空间内的统一坐标体系,「世界」用来表示我们的游戏场景。
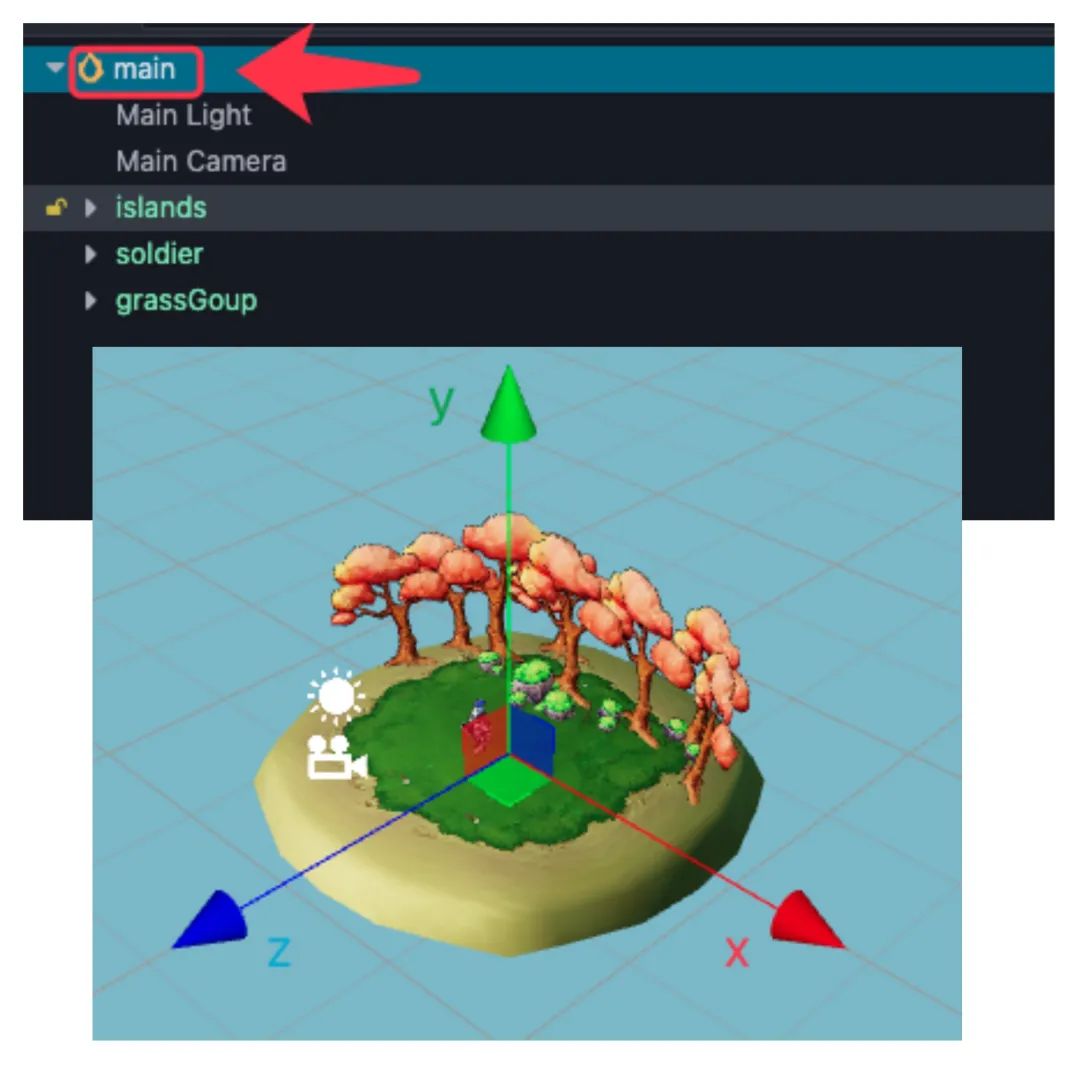
Cocos Creator 世界坐标系
物体坐标系
物体坐标系(Local Coordinate)是和特定物体相关的坐标系。每个物体都有它们独立的坐标系,当物体移动或改变方向时,和物体相关的坐标系也会改变。
某些情况下,物体坐标系也称为模型坐标系。因为模型顶点的坐标时在模型坐标中描述的。
物体坐标系 | 本地坐标系 | 模型坐标系 | 局部坐标系 可以看作一个东西多种叫法。
在物体坐标系中可能遇到的问题:
周围有相互作用的物体吗?(我要攻击它吗)
哪个方向?在我的前面后面?左边?右边?(我应该向它射击🔫,,还是转身就跑🏃?)
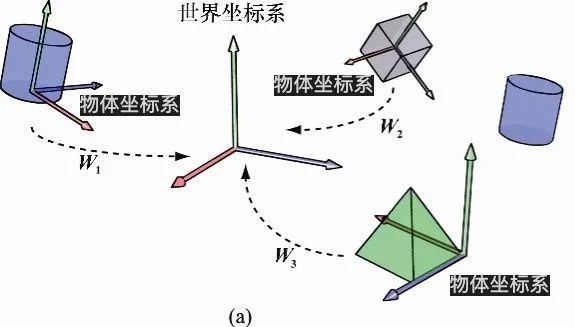
物体坐标系
模型定义的空间叫作局部空间(local space)或模型空间(model space)。OpenGL 文档使用的术语是物体空间(object space)。
🥥 Cocos Creator 3.0 的 节点(Node)之间可以有父子关系的层级结构,我们通过修改节点的 Position 属性设定的节点位置是该节点相对于父节点的本地坐标系,而非世界坐标系。
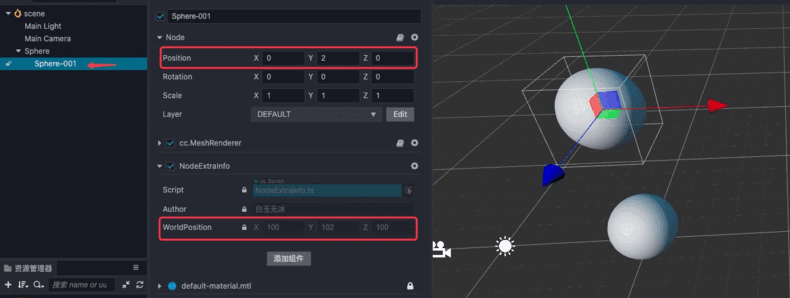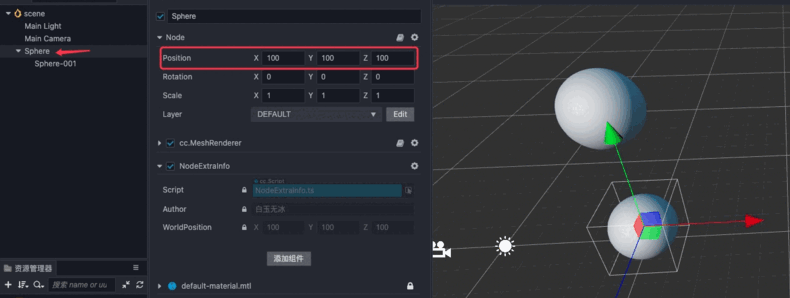
Cocos Creator 本地坐标系
3D 美工们在构筑 3D 对象时也在做着类似的事情。他们并不会在全局场景坐标系(即世界空间,也译为世界坐标系,world space)中构建物体的几何形状,而是相对于局部坐标系(局部空间,也译为局部坐标系,local space)来创建物体。
摄像机坐标系
摄像机坐标系可被看作是一种特殊的物体坐标系,该物体坐标系就定义在摄像机的屏幕可见区域。
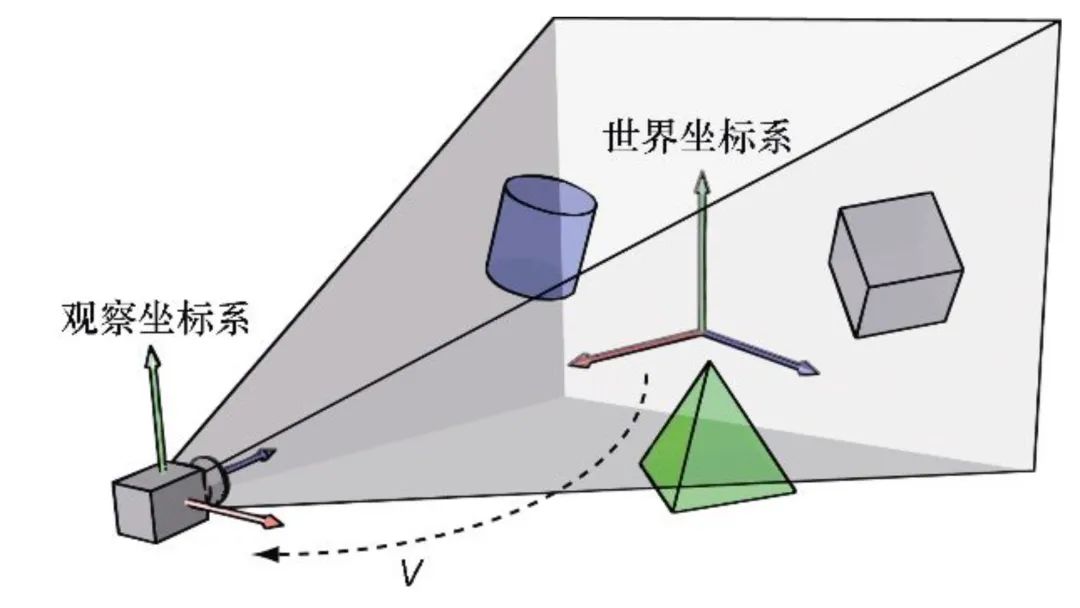
摄像机坐标系
关于摄像机坐标系的一些典型问题:
3D 空间中的某个点是在摄像机的前方吗?
3D 空间中的某个点是在屏幕上,还是超出了摄像机平界面锥体的边界?(裁剪坐标系)
某个物体是否在屏幕上?是部分在,还是全部不在?
两个物体,谁在前面?(可见性检测)
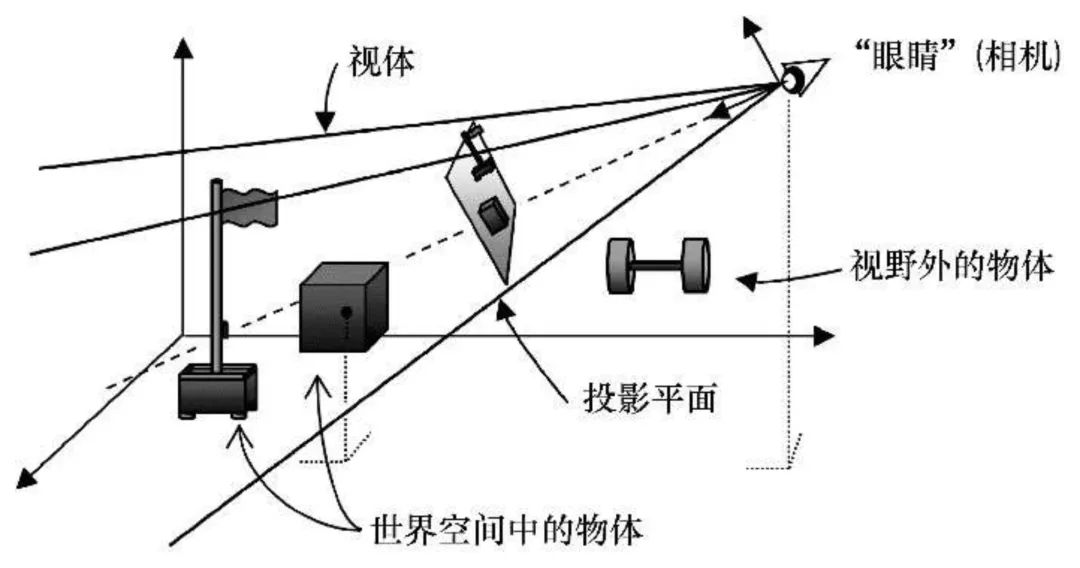
摄像机坐标系
我们为摄像机赋予一个局部坐标系(这被称作观察空间(view space),也译作观察坐标系、视图空间、视觉空间(eye space)或摄像机空间(camera space)。
🥥 相机的可视范围是通过6个平面组成一个视锥体(Frustum)构成,近裁剪面(Near Plane)和远裁剪面(Far Plane)用于控制近处和远处的可视距离与范围,同时它们也构成了视口的大小。
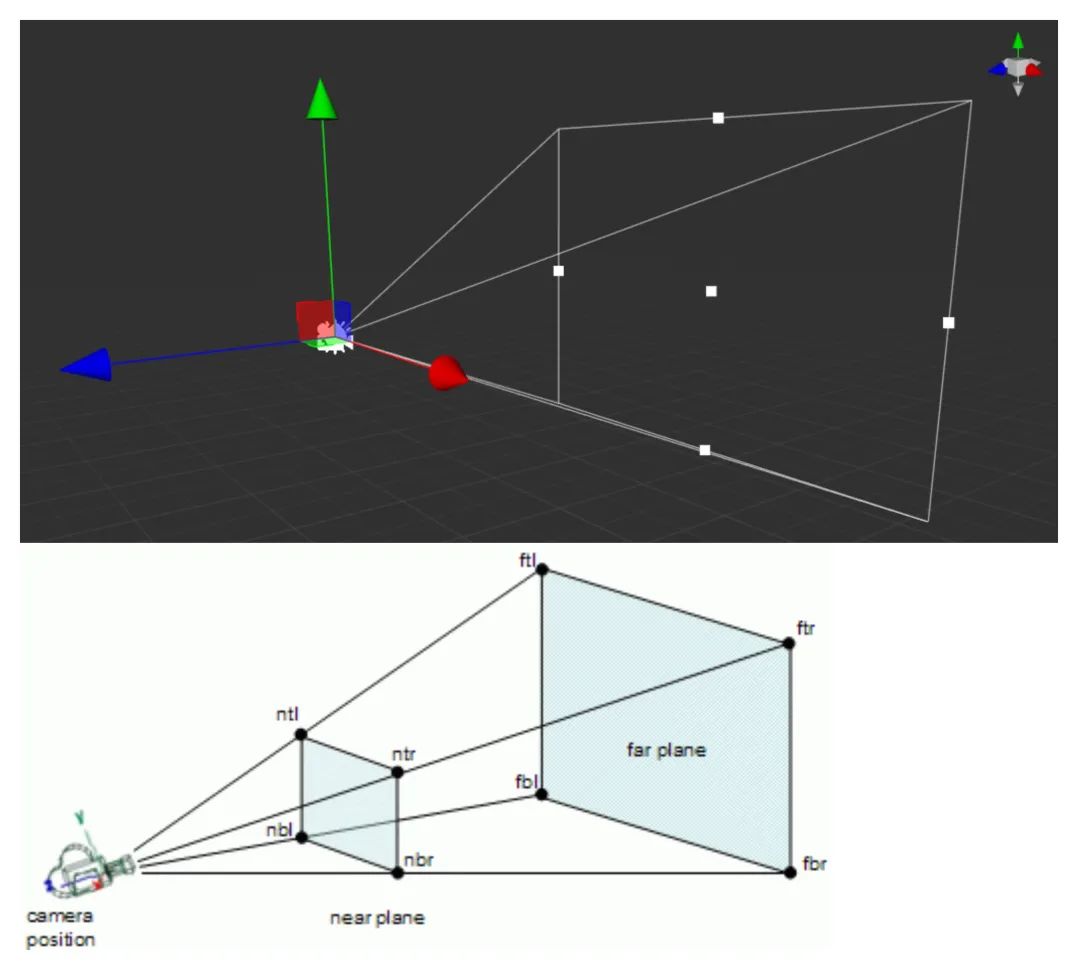
摄像机
坐标系转换
坐标变换:知道某一点的坐标,怎样在另一个坐标系中描述该点。该点并没有真正移动,而是在不同的坐标系中描述它的位置。
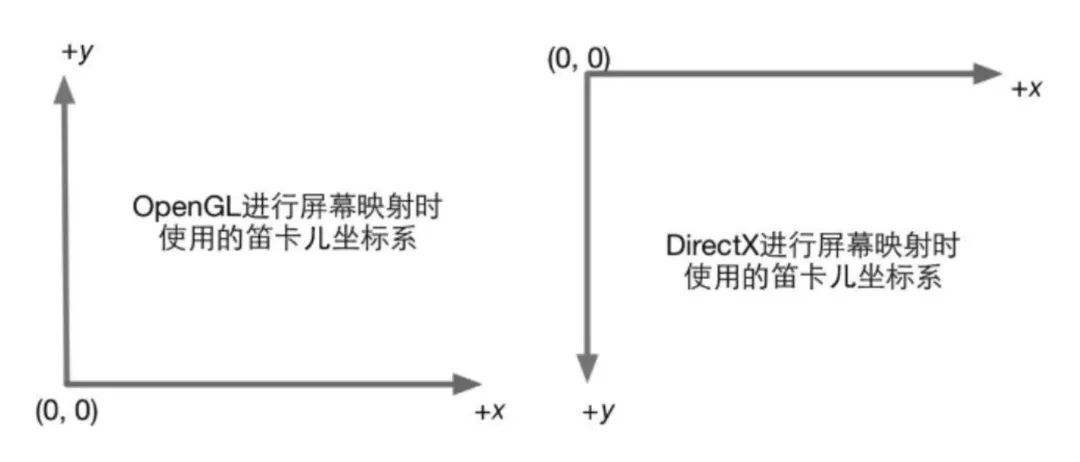
OpenGL 与 DirectX 坐标系
通常,坐标系间的变化会用矩阵(先挖个坑,后面再详细讲)表示。
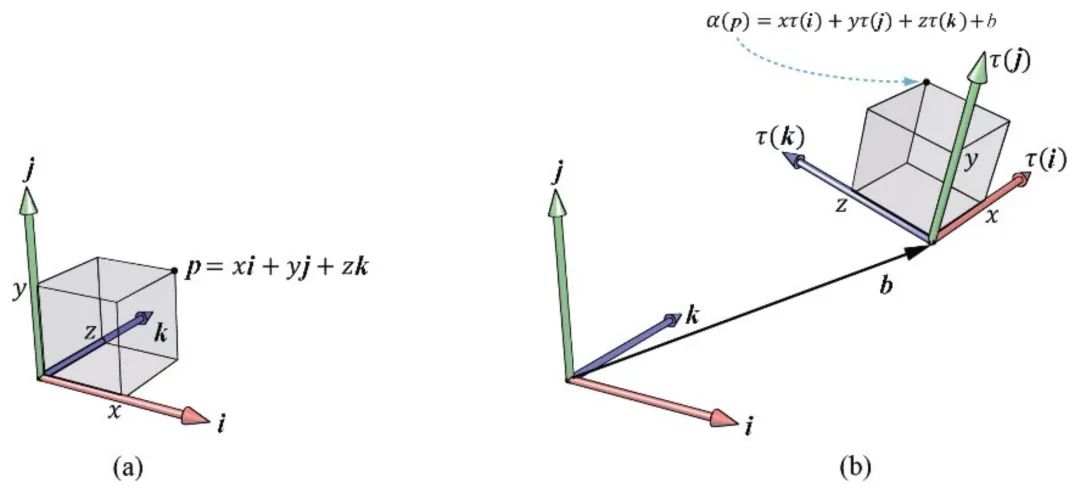
坐标变换
将局部坐标系内的坐标转换到全局场景坐标系中的过程叫作世界变换(world transform),所使用的变换矩阵名为世界矩阵(world matrix)。
那么从全局坐标转到局部坐标,就用世界矩阵的逆!
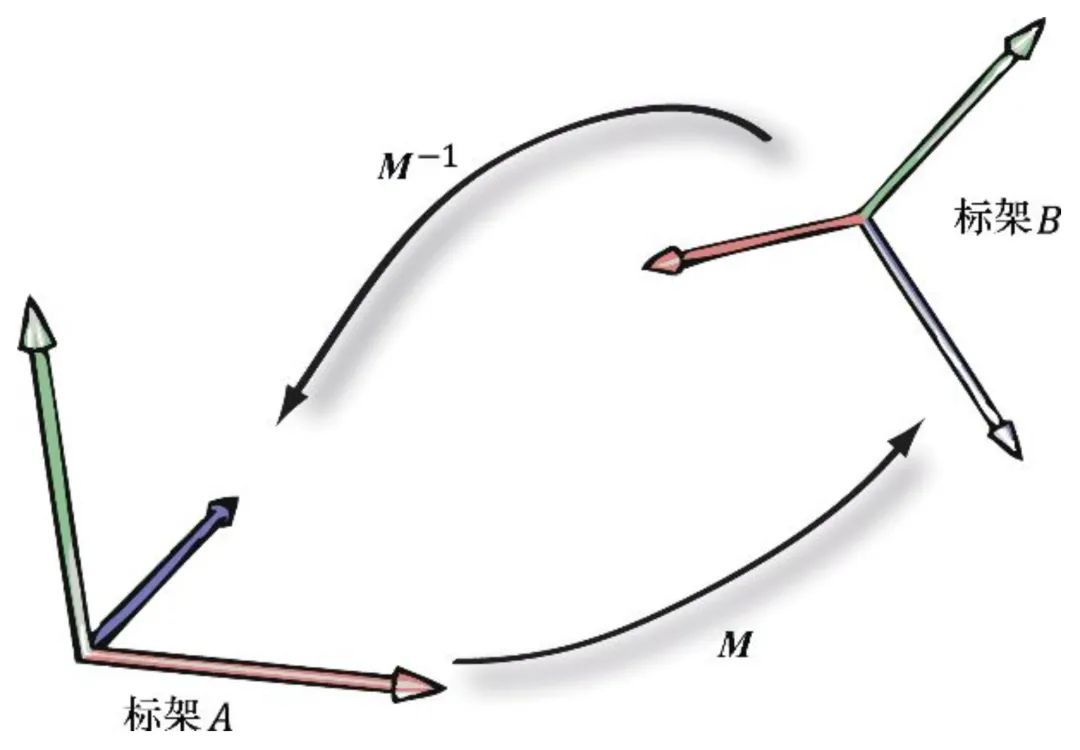
坐标变换
由世界空间至观察空间的坐标变换称为取景变换(view transform,也译作观察变换、视图变换等),此变换所用的矩阵则称为观察矩阵(view matrix,亦译作视图矩阵)。
摄像机也是属于局部坐标的一种,也就是说,观察矩阵等同于相机的世界矩阵的逆!
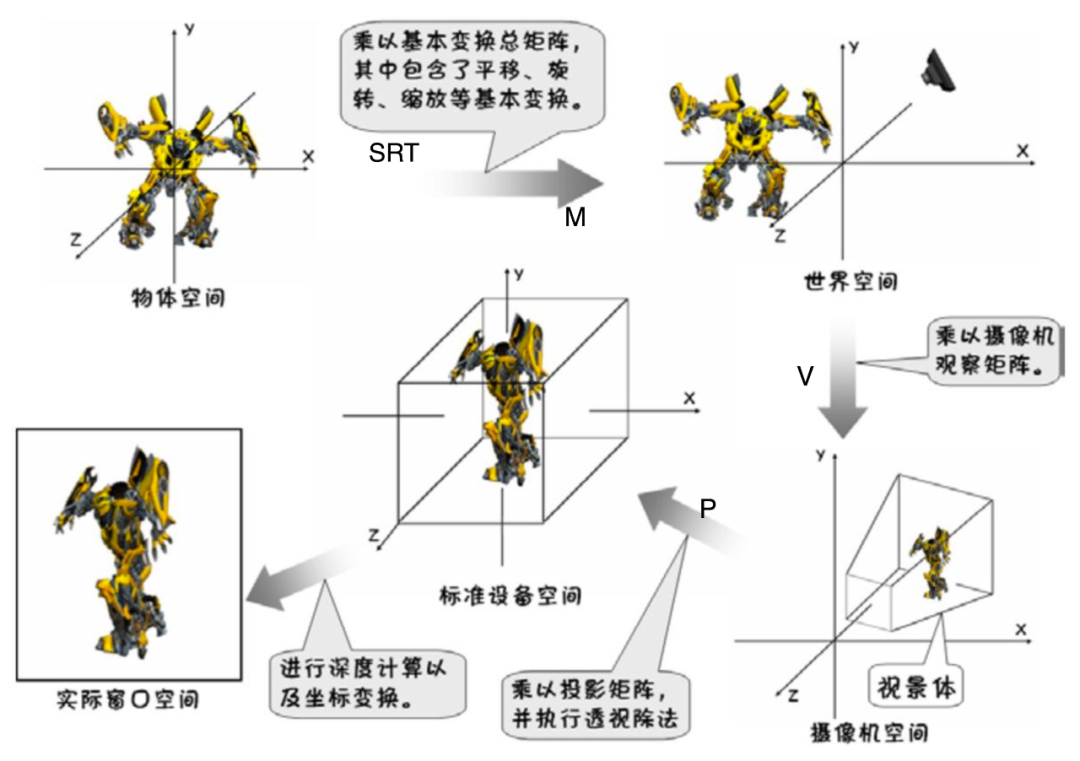
SRT MVP
举个例子,场景中的有两个节点,他们各自有一个子节点,求其中一个子节点在另一个子节点的局部坐标系中的坐标。
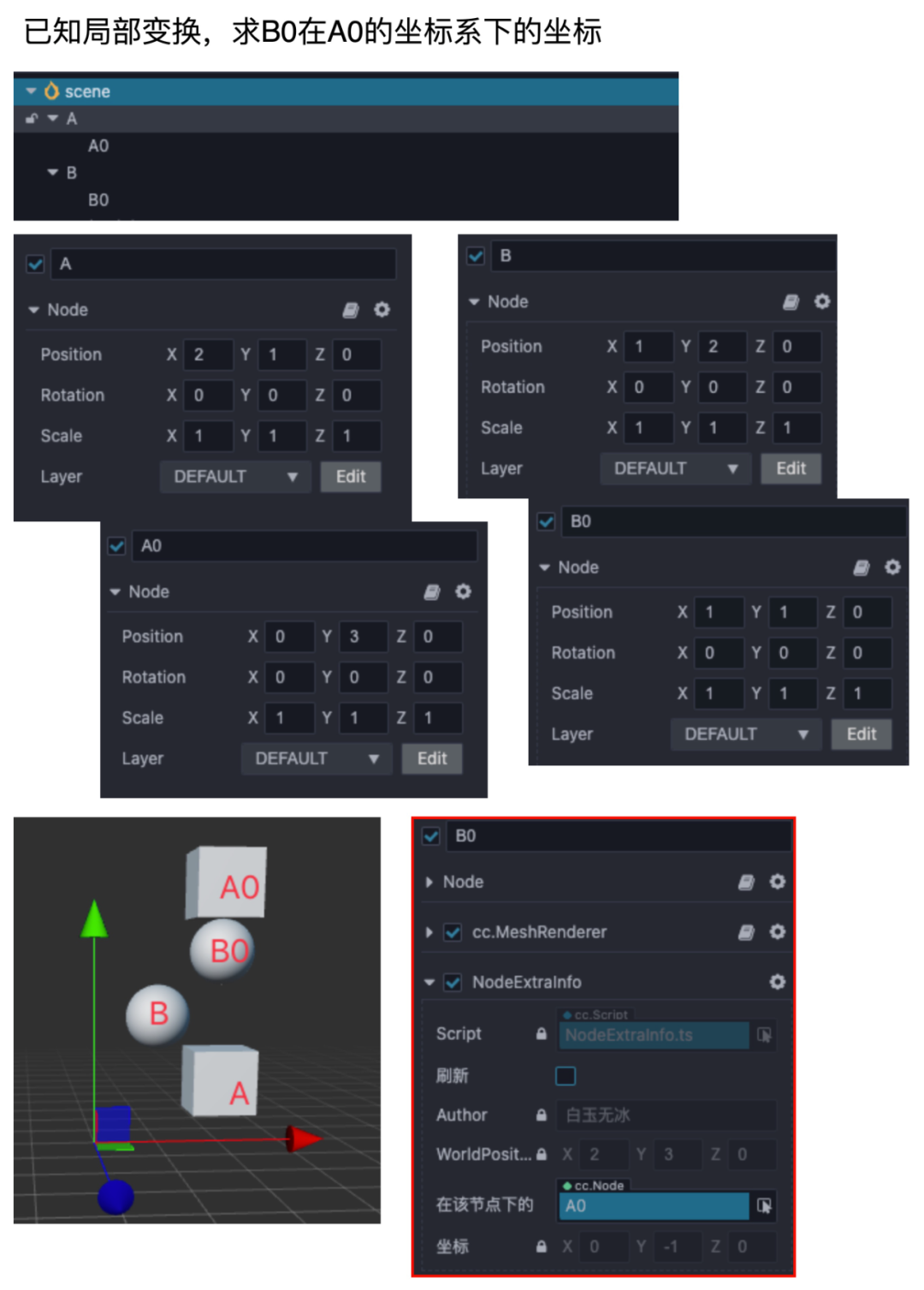
举个例子
分三步走,解决上述例子:
求出 B0 的世界坐标
求出 A0 的世界矩阵的逆
将上面两步的结果相乘
aW1wb3J0IHsgX2RlY29yYXRvciwgQ29tcG9uZW50LCBOb2RlLCBWZWMzLCB2MywgbWF0NCwgTWF0NCB9IGZyb20gJ2NjJzsKaW1wb3J0IHsgRURJVE9SIH0gZnJvbSAnY2MvZW52JzsKY29uc3QgeyBjY2NsYXNzLCBwcm9wZXJ0eSwgZXhlY3V0ZUluRWRpdE1vZGUgfSA9IF9kZWNvcmF0b3I7Cgpjb25zdCB0ZW1wX21hdDQgPSBtYXQ0KCk7CkBjY2NsYXNzKCdOb2RlRXh0cmFJbmZvJykKQGV4ZWN1dGVJbkVkaXRNb2RlCmV4cG9ydCBjbGFzcyBOb2RlRXh0cmFJbmZvIGV4dGVuZHMgQ29tcG9uZW50IHsKCiAgICBAcHJvcGVydHkKICAgIHByaXZhdGUgX3JlZnJlc2ggPSBmYWxzZTsKICAgIEBwcm9wZXJ0eSh7ZGlzcGxheU5hbWU6ICLliLfmlrAifSkKICAgIGdldCByZWZyZXNoKCkgewogICAgICAgIHJldHVybiB0aGlzLl9yZWZyZXNoOwogICAgfQogICAgc2V0IHJlZnJlc2godmFsdWUpIHsKICAgICAgICB0aGlzLm9uVHJhbnNmb3JtQ2hhbmdlKCkKICAgIH0KCiAgICBAcHJvcGVydHkoeyByZWFkb25seTogdHJ1ZSwgZWRpdG9yT25seTogdHJ1ZSB9KQogICAgQXV0aG9yID0gIueZveeOieaXoOWGsCI7CgogICAgQHByb3BlcnR5KHsgcmVhZG9ubHk6IHRydWUsIGVkaXRvck9ubHk6IHRydWUgfSkKICAgIHdvcmxkUG9zaXRpb246IFZlYzMgPSB2MygpOwoKICAgIEBwcm9wZXJ0eSh7IGVkaXRvck9ubHk6IHRydWUsIGRpc3BsYXlOYW1lOiAi5Zyo6K+l6IqC54K55LiL55qEIiwgdHlwZTogTm9kZSB9KQogICAgb3RoZXJOb2RlOiBOb2RlID0gbnVsbCE7CgogICAgQHByb3BlcnR5KHsgcmVhZG9ubHk6IHRydWUsIGVkaXRvck9ubHk6IHRydWUsIGRpc3BsYXlOYW1lOiAi5Z2Q5qCHIiB9KQogICAgb3RoZXJOb2RlUG9zaXRpb246IFZlYzMgPSB2MygpOwoKICAgIG9uRW5hYmxlKCkgewogICAgICAgIGlmICghRURJVE9SKSByZXR1cm4KICAgICAgICB0aGlzLm9uVHJhbnNmb3JtQ2hhbmdlKCk7CiAgICAgICAgdGhpcy5ub2RlLm9uKE5vZGUuRXZlbnRUeXBlLlRSQU5TRk9STV9DSEFOR0VELCB0aGlzLm9uVHJhbnNmb3JtQ2hhbmdlLCB0aGlzKTsKICAgIH0KCiAgICBvbkRpc2FibGUoKSB7CiAgICAgICAgaWYgKCFFRElUT1IpIHJldHVybgogICAgICAgIHRoaXMubm9kZS5vZmYoTm9kZS5FdmVudFR5cGUuVFJBTlNGT1JNX0NIQU5HRUQsIHRoaXMub25UcmFuc2Zvcm1DaGFuZ2UsIHRoaXMpOwogICAgfQoKICAgIHByaXZhdGUgb25UcmFuc2Zvcm1DaGFuZ2UoKSB7CiAgICAgICAgdGhpcy53b3JsZFBvc2l0aW9uID0gdGhpcy5ub2RlLndvcmxkUG9zaXRpb247CiAgICAgICAgaWYgKHRoaXMub3RoZXJOb2RlKSB7CiAgICAgICAgICAgIGNvbnN0IG90aGVyTm9kZVdvcmxkTWF0cml4SW52ZXJ0ID0gTWF0NC5pbnZlcnQodGVtcF9tYXQ0LCB0aGlzLm90aGVyTm9kZS53b3JsZE1hdHJpeCk7CiAgICAgICAgICAgIFZlYzMudHJhbnNmb3JtTWF0NCh0aGlzLm90aGVyTm9kZVBvc2l0aW9uLCB0aGlzLndvcmxkUG9zaXRpb24sIG90aGVyTm9kZVdvcmxkTWF0cml4SW52ZXJ0KTsKICAgICAgICB9CiAgICB9Cn0=
复平面
刚好讲到坐标系,这边扯点其他相关的东西。
在复平面中,有一个实轴和一个虚轴。复数的乘积的几何意义刚好是旋转与缩放。
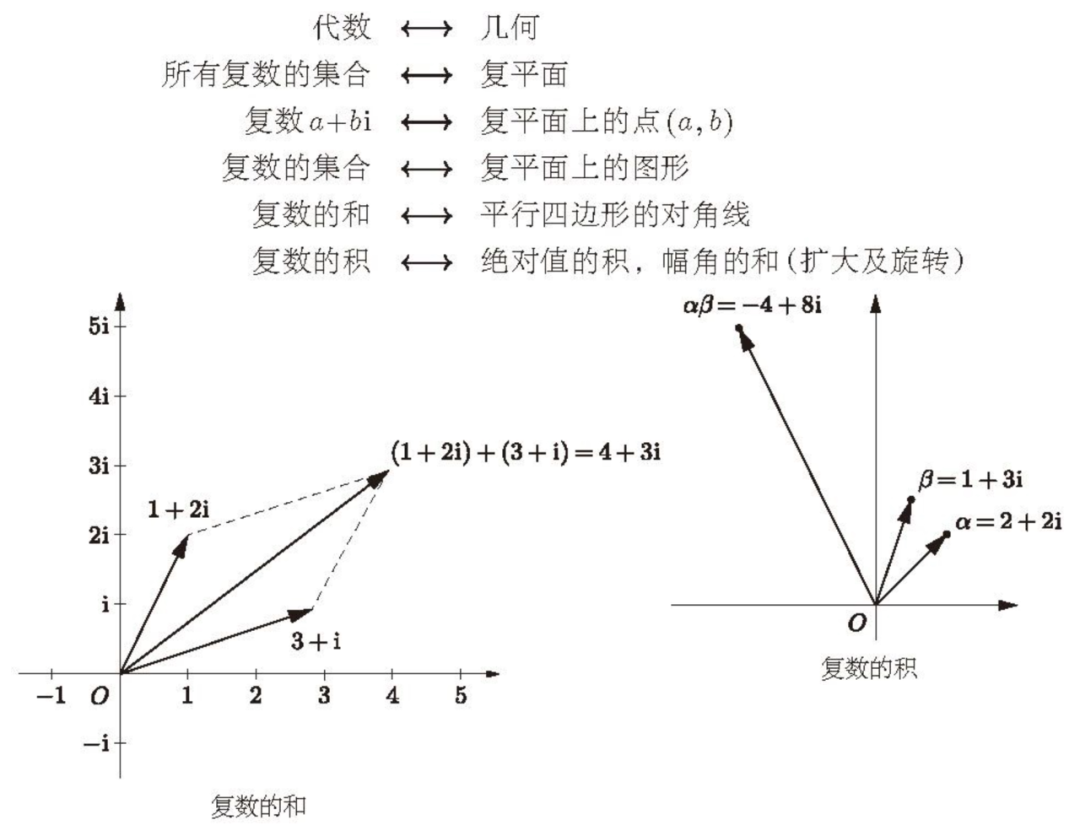
复平面
坐标系的部分到此暂时告一段落,下一期白玉无冰预计会写关于向量的笔记。欢迎持续关注我的公众号!
参考资料
《3D 数学基础:图形与游戏开发》
《游戏引擎架构》
《DirectX 12 3D 游戏开发实战》
《数学女孩》
往期精彩



