为什么函数y=f(x)的导数dy/dx可以适用分数运算呢?

一、问题背景

在同济大学高等数学关于导数的内容中，如果函数y=f(x)可以由参数方程：

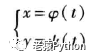
表示，且三个函数皆可导，且x的值不为0，则：

才开始看这个公式推导时，觉得没什么问题，仔细一想，dy/dx是导数的表示符号，为什么这个符号可以适用分数运算公式呢？二者难道可以拆分吗？下面我们就来分析一下。

二、证明

为了好书写，下面用x=g(t)、y=h(t)在点x0的导数来推导一下：

假设在函数x=g(t)中，x0的值对应t0，则：

dy/dx=（f(x)-f(x0)）/(x-x0))=(h(t)-h(t0))/(g(t)-g(t0))

上式右边分子分母同时除以（t-t0）:

dy/dx=((h(t)-h(t0))/(t-t0))/((g(t)-g(t0))/(t-t0))

即得到：dy/dx=（dy/dt）/(dx/dt) = h’(t)/g’(t)

相关问题得证。

三、小结：

本文证明了由变量t对应参数方程指定的函数y=f(x)的导数等于该函数自变量和因变量相对于t的导数的商。

说明：

本文内容是老猿学习同济版高数的总结，有需要原教材电子版以及OpenCV、Python基础知识、、图像处理原理介绍相关电子资料，或对文章内有有疑问咨询的，请扫博客首页左边二维码加微信公号，根据加微信公号后的自动回复操作。

更多人工智能数学基础请参考专栏《人工智能数学基础》。