为什么多元向量函数的导数是个矩阵-轻识

那是因为要求函数可微，而这个要求其实挺高的。

1函数可微性

微积分的基本理念是利用仿射函数对函数进行近似。如果存在线性函数和向量，使得对于任意，都有

\mathcal{A}({x})=\mathcal{L}({x})+{y}

那么称函数是一个仿射函数。

给定函数和点，希望找到一个仿射函数，使其在点附近能够近似函数。首先，显然仿射函数应该满足

\mathcal{A}\left({x}_{0}\right)={f}\left({x}_{0}\right)

由，可得

{y}={f}\left({x}_{0}\right)-\mathcal{L}\left({x}_{0}\right)

于是

\begin{array}{l} \mathcal{L}({x})+{y}\!\!\!&=\mathcal{L}({x})-\mathcal{L}\left({x}_{0}\right)+{f}\left({x}_{0}\right)\\[0.8em]&=\mathcal{L}\left({x}-{x}_{0}\right)+{f}\left({x}_{0}\right) \end{array}

最后一个等式是由于是线性函数。因此，仿射函数可写为

\mathcal{A}({x})=\mathcal{L}\left({x}-{x}_{0}\right)+{f}\left({x}_{0}\right)

对于给定的函数，，在点处是可微的是指存在一个仿射函数能够在点附近近似函数。具体来说，这个近似是指存在线性函数，使得

\lim _{x \rightarrow x_{0}, x \in \Omega} \frac{\left\|{f}({x})-\left(\mathcal{L}\left({x}-{x}_{0}\right)+{f}\left({x}_{0}\right)\right)\right\|}{\left\|{x}-{x}_{0}\right\|}=0.

上式中的线性函数可由和唯一确定，称为在点的导数。

.几何解释

考虑一个的函数，如

{f}: (x,y) \rightarrow (x,y,z(x,y))

在点处的切平面是该点处各个方向上所有函数曲面与过该点并与 xy-平面垂直的平面之间的交线的切线构成的平面。

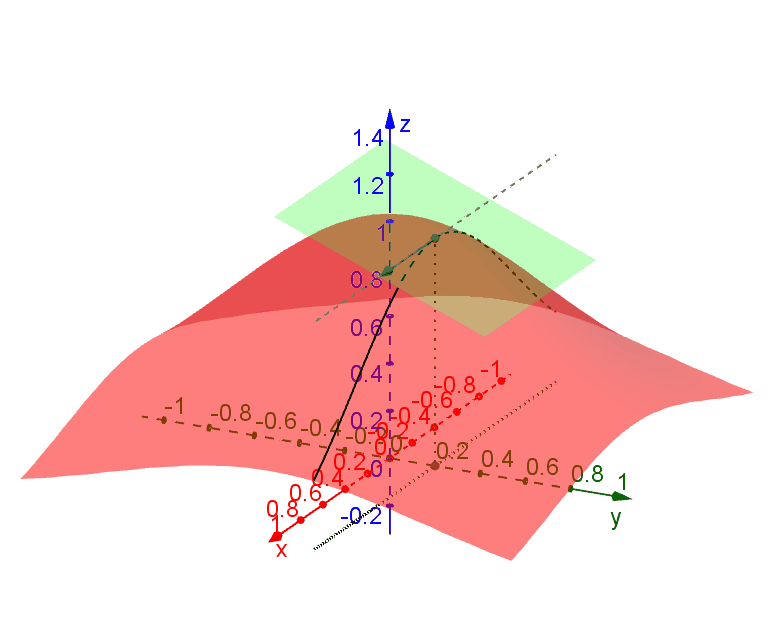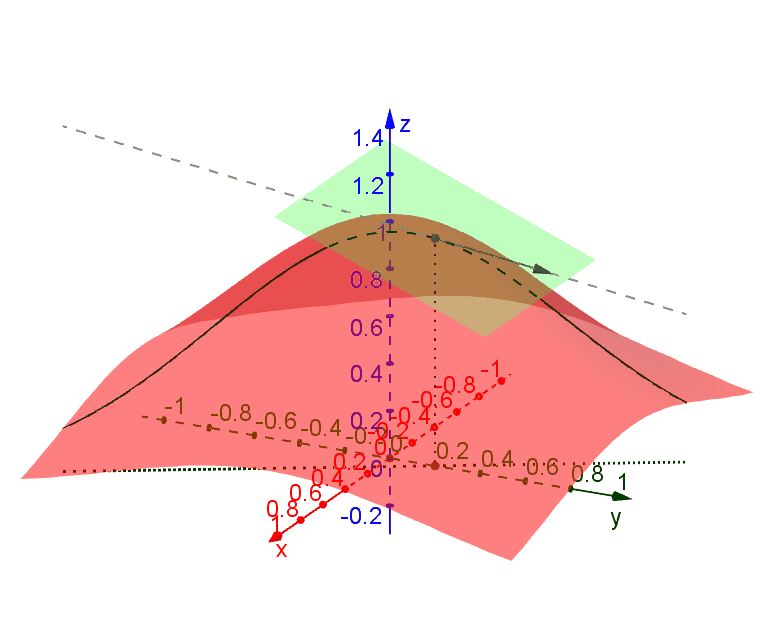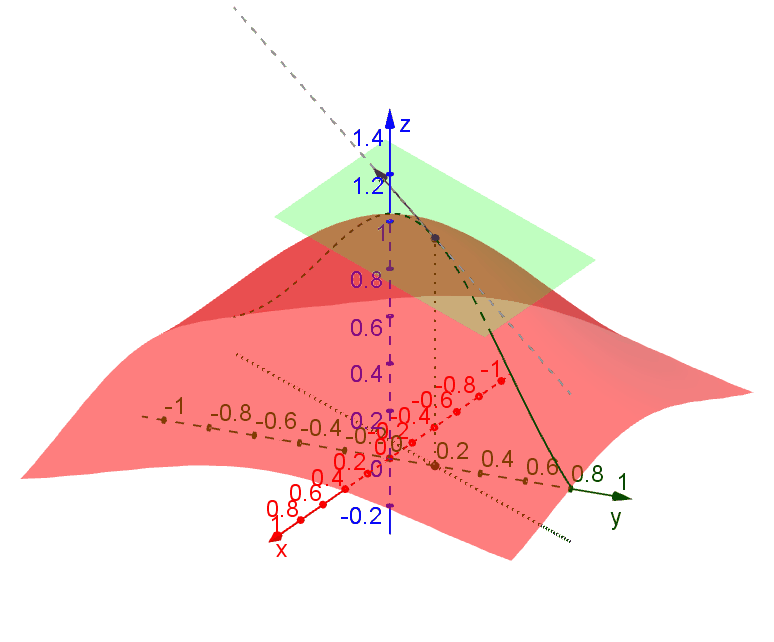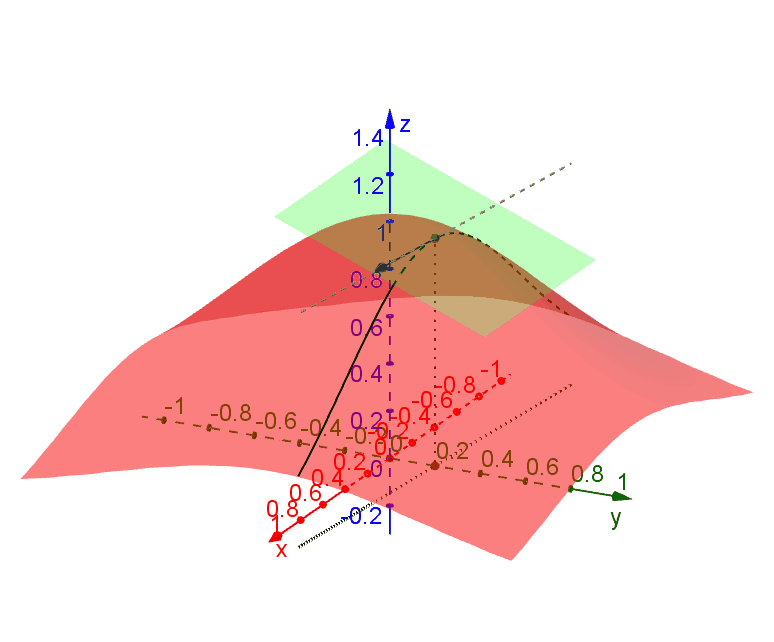
如果点处存在这样一个平面，那么我们说在点处是可微的。如果函数在定义域上处处可微，那么称在上是可微的。

不妨想象一下在一个光滑的山坡上滑雪时的情形。滑雪板的中心始终与山坡（函数曲面）相切，而你与滑雪板垂直。打个比方，可微就相当于山坡能让你顺畅地滑雪下山，而且能够选不同方向；而如果不可微，可能会让你磕磕绊绊、举步维艰。

再回头看一下一元函数的情况，

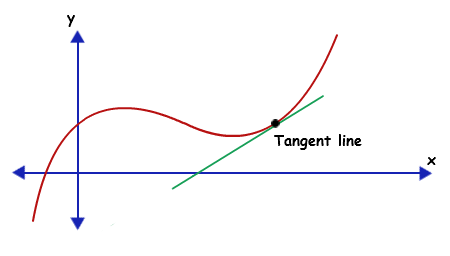
对照两个图，是否感觉到: 一元函数的导数推广到多元向量值函数上就应该是一个导数矩阵。但其实背后对应的是可微这个概念，也正是从可微性导出了雅可比矩阵。

2导数矩阵

那么上文中的线性函数到底长什么样呢？

我们知道，从到的线性变换，都可以表示为一个矩阵。为了确定可微函数的导数所对应的矩阵表示，引入空间的标准基。考虑向量

\begin{array}{ll} {x}_{j}={x}_{0}+t {e}_{j}, \quad j=1, \cdots, n \end{array}

根据导数的定义，有

\begin{array}{ll} \lim _{t \rightarrow 0} \dfrac{{f}\left({x}_{j}\right)-\left(t {L} {e}_{j}+{f}\left({x}_{0}\right)\right)}{t}=\mathbf{0} \end{array}.

这意味着，对于，有

\begin{array}{ll} \lim _{t \rightarrow 0} \dfrac{{f}\left({x}_{j}\right)-{f}\left({x}_{0}\right)}{t}={L} {e}_{j}, \end{array}

是矩阵的第列向量与仅仅在第个元素上存在差异，该元素上的差值为。因此，上式的左边等于偏导数 $\dfrac{\partial {f}}{\partial x_{j}}\left({x}_{0}\right)$ 。

可以通过向量中每个元素求极限的方式来计算向量极限。因此，如果记向量值函数

{f}({x})=\left[\begin{array}{c} f_{1}({x}) \\ \vdots \\ f_{m}({x}) \end{array}\right]

那么有

\frac{\partial {f}}{\partial x_{j}}\left({x}_{0}\right)=\left[\begin{array}{c} \frac{\partial f_{1}}{\partial x_{j}}\left({x}_{0}\right) \\ \vdots \\ \frac{\partial f_{m}}{\partial x_{j}}\left({x}_{0}\right) \end{array}\right]

矩阵可写为

\left[\dfrac{\partial {f}}{\partial x_{1}}\left({x}_{0}\right) \cdots \dfrac{\partial {f}}{\partial x_{n}}\left({x}_{0}\right)\right]=\left[\begin{array}{ccc} \dfrac{\partial f_{1}}{\partial x_{1}}\left({x}_{0}\right) & \cdots & \dfrac{\partial f_{1}}{\partial x_{n}}\left({x}_{0}\right) \\ \vdots & & \vdots \\ \dfrac{\partial f_{m}}{\partial x_{1}}\left({x}_{0}\right) & \cdots & \dfrac{\partial f_{m}}{\partial x_{n}}\left({x}_{0}\right) \end{array}\right]

矩阵称为在点的雅可比矩阵或导数矩阵，记为。有了导数矩阵，上面所说的仿射近似就可以写为，

\begin{array}{lll} {f}({x}+\delta {x}) &\approx\left[\begin{array}{c} f_{1}({x}) \\ \vdots \\ f_{m}({x}) \end{array}\right]+\left[\begin{array}{ccc} \dfrac{\partial f_{1}}{\partial x_{1}} & \cdots & \dfrac{\partial f_{1}}{\partial x_{n}} \\ \vdots & \ddots & \vdots \\ \dfrac{\partial f_{m}}{\partial x_{1}} & \cdots & \dfrac{\partial f_{m}}{\partial x_{n}} \end{array}\right]\left[\begin{array}{c} \delta x_{1} \\ \vdots \\ \delta x_{n} \end{array}\right]\\[1em]&={f}({x})+D{f}({x}) \delta {x}. \end{array}

.梯度

如果是可微的，那么函数

\nabla f({x})=\left[\begin{array}{c} \dfrac{\partial f}{\partial x_{1}}({x}) \\ \vdots \\ \dfrac{\partial f}{\partial x_{n}}({x}) \end{array}\right]=D f({x})^{\top}

称为的梯度。梯度是从一个从到的函数。

.Hessian 矩阵

给定函数，如果梯度可微，则称是二次可微的，的导数记为

D^{2} f=\left[\begin{array}{cccc} \dfrac{\partial^{2} f}{\partial x_{1}^{2}} & \dfrac{\partial^{2} f}{\partial x_{2} \partial x_{1}} & \cdots & \dfrac{\partial^{2} f}{\partial x_{n} \partial x_{1}} \\ \dfrac{\partial^{2} f}{\partial x_{1} \partial x_{2}} & \dfrac{\partial^{2} f}{\partial x_{2}^{2}} & \cdots & \dfrac{\partial^{2} f}{\partial x_{n} \partial x_{2}} \\ \vdots & \vdots & \ddots & \vdots \\ \dfrac{\partial^{2} f}{\partial x_{1} \partial x_{n}} & \dfrac{\partial^{2} f}{\partial x_{2} \partial x_{n}} & \cdots & \dfrac{\partial^{2} f}{\partial x_{n}^{2}} \end{array}\right]

其中，表示首先对求导，再对求导的偏导数。矩阵称为在点的 Hessian 矩阵。

.思考

用上面这些概念可以得出多元函数的二阶近似，

\begin{array}{ll}   f({x}) \approx f({x}_0) + Df({x}_0) ({x}-{x}_0)   +  \dfrac{1}{2} ({x}-{x}_0)^{\top} D^2f({x}_0) ({x}-{x}_0). \end{array}

那如果是一个多元向量值函数呢，近似形式会是什么样子呢？

3微分法则

利用函数和函数可构成复合函数，对其进行微分可以使用链式法则。

.链式法则

如果在开集上是可微的，且在上可微。那么它们的复合函数在上是可微的，且导数为

h^{\prime}(t)=D g({f}(t)) D {f}(t)=\nabla g({f}(t))^{\top}\left[\begin{array}{c} f_{1}^{\prime}(t) \\ \vdots \\ f_{n}^{\prime}(t) \end{array}\right]

.乘积法则

令和表示两个可微函数，另有函数可定义为，那么也是可微的，且

D h({x})={f}({x})^{\top} D {g}({x})+{g}({x})^{\top} D {f}({x}).

.例子

给定矩阵，计算。

我们令，，使用上面乘积法则可得，

D\left({x}^{\top} {A} {x}\right)={x}^{\top}\left({A}+{A}^{\top}\right). \qquad (1)

如果是对称矩阵，那么可推知

D\left({x}^{\top} {Q} {x}\right)=2 {x}^{\top} {Q}.

特别的，当时，有

D\left({x}^{\top} {x}\right)=2 {x}^{\top}.

4应用举例

已知矩阵以及，考虑如下最小二乘问题，

\min_{x}\|Ax-y\|_2^2

即要你求解使最小的。

将目标函数改写为，

\begin{array}{ll} f(x)&=\|Ax-y\|_2^2 \\[0.8em]&= \langle Ax-y,Ax-y\rangle\\[0.8em]&=(Ax-y)^{\top}(Ax-y)\\[0.8em]&=(x^{\top}A^{\top}-y^{\top})(Ax-y)\\[0.8em]&=x^{\top}A^{\top}Ax-x^{\top}A^{\top}y-y^{\top}Ax+y^{\top}y \end{array}

我们知道，为该函数的极小值点的必要条件是。由式可知该导数为，

Df(x_0)=2x_0^{\top}A^{\top}A - 2y^{\top}A

上式为可得，

x_0^{\top}A^{\top}A = y^{\top}A

两边转置得，

A^{\top}Ax_0 = A^{\top}y

这正是法方程（normal equation），至于它有没有唯一解，那就要看矩阵了。

⟳参考资料⟲

[1]

Tangent plane: http://www.math.ubc.ca/~cwsei/math200/graphics/tangentplane.html

[2]

An Introduction to Optimization, Edwin K. P. Chong and Stanislaw H. Żak.: https://www.engr.colostate.edu/~echong/book4/

为什么多元向量函数的导数是个矩阵