借助可视化，最直观理解梯度，以及偏导数、方向导数和法向量等

写在前面

梯度是微积分中的基本概念，也是机器学习解优化问题经常使用的数学工具（梯度下降算法），虽然常说常听常见，但其细节、物理意义以及几何解释还是值得深挖一下，这些不清楚，梯度就成了“熟悉的陌生人”，仅仅“记住就完了”在用时难免会感觉不踏实，为了“用得放心”，本文将尝试直观地回答以下几个问题，

• 梯度与偏导数的关系？
• 梯度与方向导数的关系？
• 为什么说梯度方向是上升最快的方向，负梯度方向为下降最快的方向？
• 梯度的模有什么物理意义？
• 等高线图中绘制的梯度为什么垂直于等高线？
• 全微分与隐函数的梯度有什么关系？
• 梯度为什么有时又成了法向量？

闲话少说，书归正传。在全篇“作用域”内，假定函数可导。

偏导数

在博文《单变量微分、导数与链式法则》（https://www.cnblogs.com/shine-lee/p/10324601.html）中，我们回顾了常见初等函数的导数，概括地说，

导数是一元函数的变化率（斜率）。导数也是函数，是函数的变化率与位置的关系。

如果是多元函数呢？则为偏导数。

偏导数是多元函数“退化”成一元函数时的导数，这里“退化”的意思是固定其他变量的值，只保留一个变量，依次保留每个变量，则  元函数有 个偏导数。

以二元函数为例，令，绘制在3维坐标系如下图所示，

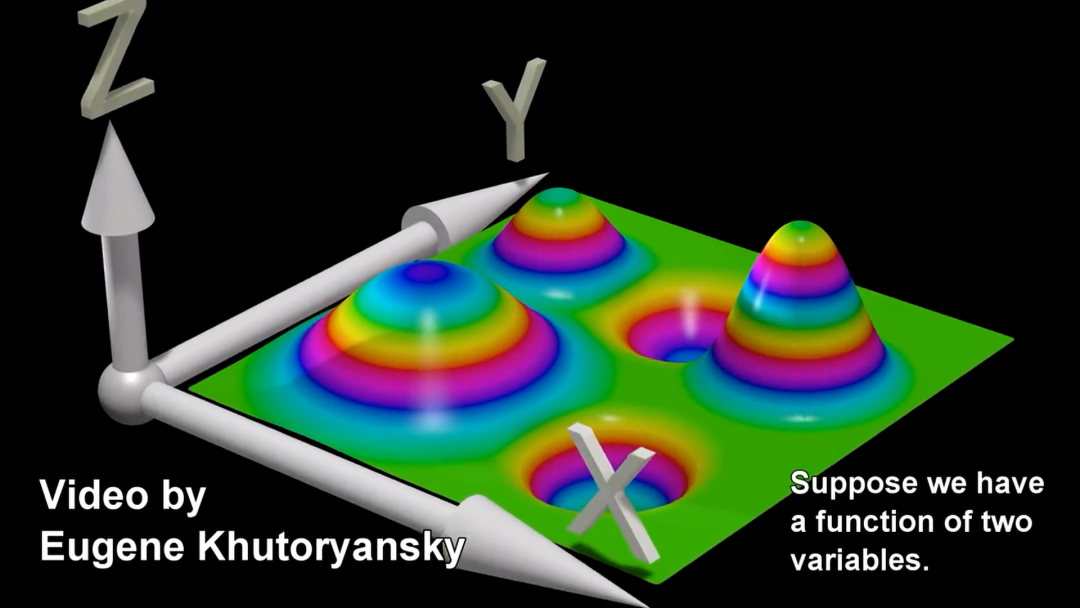
在分别固定 和 的取值后得到下图中的黑色曲线——“退化”为一元函数，二维坐标系中的曲线——则偏导数 和 分别为曲线的导数（切线斜率）。

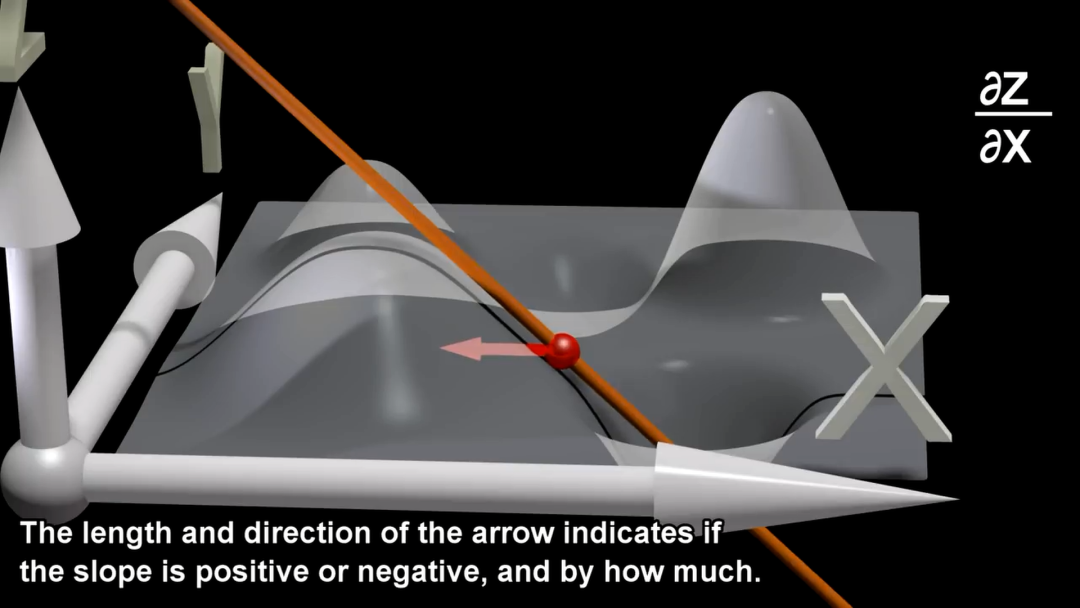
由上可知，一个变量对应一个坐标轴，偏导数为函数在每个位置处沿着自变量坐标轴方向上的导数（切线斜率）。

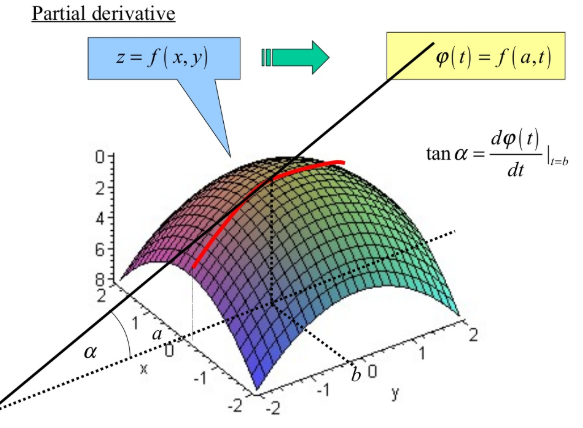
方向导数

如果是方向不是沿着坐标轴方向，而是任意方向呢？则为方向导数。如下图所示，点 位置处红色箭头方向的方向导数为黑色切线的斜率，来自链接

Directional Derivative

https://www.geogebra.org/m/Bx8nFMNc

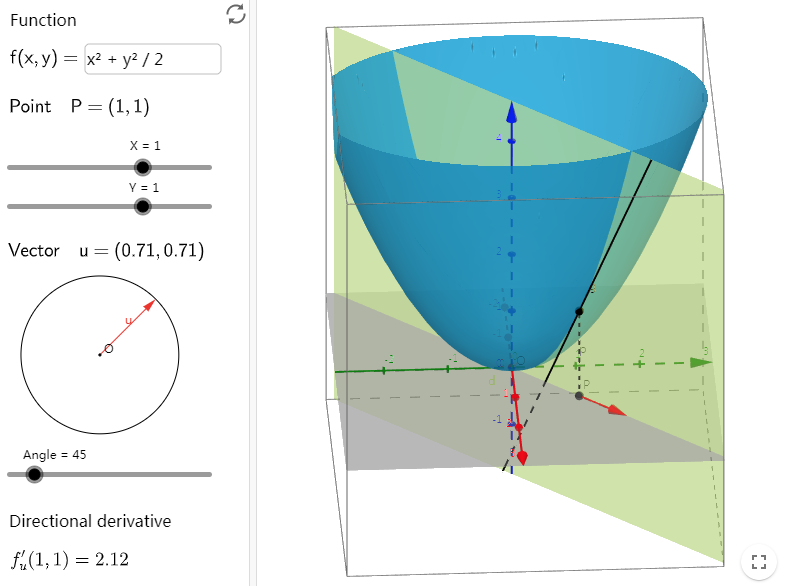
方向导数为函数在某一个方向上的导数，具体地，定义平面上一点(  以及单位向量 在曲面 上， 从点  出发，  沿方向走  单位长度后， 函数值  为  则点  处  方向的方向导数为 :

上面推导中使用了链式法则。其中， 和 分别为函数在 位置的偏导数。由上面的推导可知：

该位置处，任意方向的方向导数为偏导数的线性组合，系数为该方向的单位向量。当该方向与坐标轴正方向一致时，方向导数即偏导数，换句话说，偏导数为坐标轴方向上的方向导数，其他方向的方向导数为偏导数的合成。

写成向量形式，偏导数构成的向量为 称之为 梯度

梯度

梯度，写作 二元时为 多元时为 。

我们继续上面方向导数的推导， 处  方向上的方向导数为

其中，  为  与  的夹角，显然，当  即  与梯度  同向时，方向导数取得最大值，最大值为梯度的模  当  即  与梯度  反向时，方向导数取得最小值，最小值为梯度模的相反数。此外 根据上面方向导数的公式可知，在夹角  时方向导数为正，表示  方向函数值上升，  时方向导数为负, 表示该方向函数值下降。

至此，方才有了梯度的几何意义：

1. 当前位置的梯度方向，为函数在该位置处方向导数最大的方向，也是函数值上升最快的方向，反方向为下降最快的方向；
2. 当前位置的梯度长度（模），为最大方向导数的值。

等高线图中的梯度

在讲解各种优化算法时，我们经常看到目标函数的等高线图示意图，如下图所示，来自链接

Applet: Gradient and directional derivative on a mountain

https://mathinsight.org/applet/gradient_directional_derivative_mountain

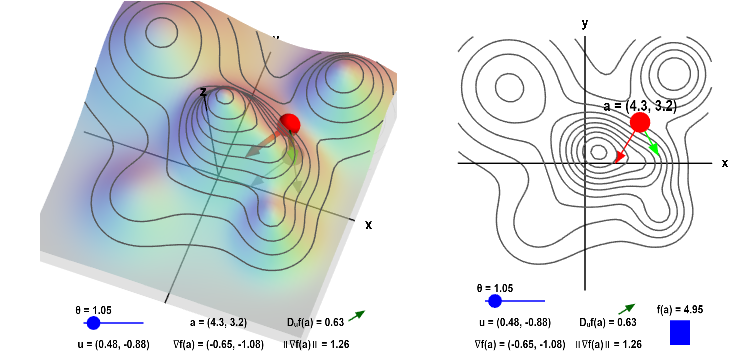
图中，红点为当前位置，红色箭头为梯度，绿色箭头为其他方向，其与梯度的夹角为 。

将左图中 曲面上的等高线投影到 平面，得到右图的等高线图。

梯度与等高线垂直。为什么呢?

等高线，顾名思义，即这条线上的点高度（函数值）相同，令某一条等高线为 C为常数，两边同时全微分，如下所示

这里，两边同时全微分的几何含义是，在当前等高线上挪动任意一个极小单元，等号两侧的变化量相同。 的 变化量有两个来源，一个由x的变化带来，另一个由y的变化带来，在一阶情况下，由 带来的变化量为 由 带来的变化量为 两者叠加为z的总变化量，等号右侧为常数，因为我们指定在当前等高线上挪动一个极小单元，其变化量为0，左侧等于右侧。进一步拆分成向量内积形式，( )为梯度， 为该点指向任意方向 的极小向量，因为两者内积为0，所以两者垂直。自然不难得出梯度与等高线垂直的结论。

更进一步地，梯度方向指向函数上升最快的方向，在等高线图中，梯度指向高度更高的等高线。

隐函数的梯度

同理，对于隐函数 也可以看成是一种等高线。二元时，两边同时微分，梯度垂直于曲线，多元时，两边同时微分，梯度垂直于高维曲面。

即，隐函数的梯度为其高维曲面的法向量。

有了法向量，切线或切平面也就不难计算得到了。令曲线 上一点为 通过全微分得该点的梯度为 则该点处的切线为 相当于将上面的微分向量 替换为 其几何意义为法向量垂直切平面上的任意向量。

小结

至此，文章开篇几个问题的答案就不难得出了，

• 偏导数构成的向量为梯度；
• 方向导数为梯度在该方向上的合成，系数为该方向的单位向量；
• 梯度方向为方向导数最大的方向，梯度的模为最大的方向导数；
• 微分的结果为梯度与微分向量的内积
• 等高线全微分的结果为0，所以其梯度垂直于等高线，同时指向高度更高的等高线
• 隐函数可以看成是一种等高线，其梯度为高维曲面（曲线）的法向量

以上。

参考

• Gradients and Partial Derivatives
• Directional Derivative
• Applet: Gradient and directional derivative on a mountain
• Gradient descent
• Gradient
• Partial derivative
• ppt Partial derivative