人工智能数学基础--导数1：基础概念及运算

一、导数的定义

导数（Derivative），也叫导函数值。又名微商，是微积分中的重要基础概念。当函数y=f（x）的自变量x在一点x0上产生一个增量Δx时，函数输出值的增量Δy与自变量增量Δx的比值在Δx趋于0时的极限a如果存在，a即为在x0处的导数，记作f’(x0)或

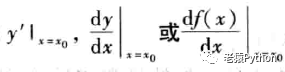
函数在定义域中一点可导需要一定的条件是：函数在该点的左右两侧导数都存在且相等。

导数是函数的局部性质。一个函数在某一点的导数描述了这个函数在这一点附近的变化率。如果函数的自变量和取值都是实数的话，函数在某一点的导数就是该函数所代表的曲线在这一点上的切线斜率。导数的本质是通过极限的概念对函数进行局部的线性逼近。

寻找已知的函数在某点的导数或其导函数的过程称为求导。实质上，求导就是一个求极限的过程，导数的四则运算法则也来源于极限的四则运算法则。

不是所有的函数都有导数，一个函数也不一定在所有的点上都有导数。若某函数在某一点导数存在，则称其在这一点可导，否则称为不可导。然而，可导的函数一定连续；不连续的函数一定不可导；连续函数不一定都可导。

如果函数在开区间I内的每点都可导，那么称该函数在开区间I内可导。

如果函数f(x)在(a,b)中每一点处都可导，则称f(x)在(a,b)上可导，则可建立f(x)的导函数，简称导数，记为f’(x)。如果f(x)在(a,b)内可导，且在区间端点a处的右导数和端点b处的左导数都存在，则称f(x)在闭区间[a,b]上可导，f’(x)为区间[a,b]上的导函数，简称导数。导函数的定义表达式为：

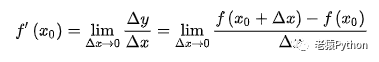
下列公式与上面公式等价：

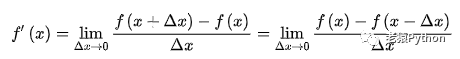
左导数和右导数统称为单侧导数，分别记为：

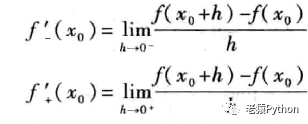
导数的几何意义：

从本质上说，函数y=f(x)在点x0处的导数在几何上表示曲线y=f(x)在点（x0，f(x0))处的切线的斜率。即f’(x0)=tan α，其中α为切线与x轴的夹角。

曲线y=f(x)在点（x0，f(x0))处对应的切线方程为：y-y0=f’(x0)(x-x0)。

与切线在切点垂直的线为法线，法线的斜率为该点导数的导数的相反数。即曲线y=f(x)在点（x0，f(x0))处对应的法线方程为：y-y0=-(x-x0)/f’(x0)。

二、基本初等函数求导公式

三、函数的和、差、积、商求导法则

四、链式法则和反函数求导法则

4.1、链式法则

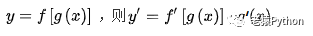
这个结论可推广到任意有限个函数复合到情形，于是复合函数的导数将是构成复合这有限个函数在相应点的 导数的乘积，就像锁链一样一环套一环，故称链式法则。

4.2、反函数求导法则

反函数的导数是原函数导数的倒数。y=f(x) 的反函数是x=g(y) ，则有：g’(y) = 1/f’(x)。

五、导数的极值

一般地，设函数y=f(x)在x=x0及其附近有定义，如果f(x0)的值比附近所有各点的函数值都大，我们说f(x0)是函数y=f(x)的一个极大值；如果f(x0)的值比附近所有各点的函数值都小，我们说f(x0)是函数y=f(x)的一个极小值。极大值与极小值统称极值。

在定义中，取得极值的点称为极值点，极值点是自变量的值，极值指的是函数值。

小结：

本文介绍了导数的定义、导数运算公式及导数的极值定义。

写博不易，敬请支持：

如果阅读本文于您有所获，敬请点赞、评论、收藏，谢谢大家的支持！