人工智能数学基础：泰勒（Taylor）公式

一、引言

对于一些较复杂的函数，为了便于研究，往往希望用一些简单的函数来近似表达，例如：

当x->0时，sinx≈arcsinx≈tanx≈arctanx≈ln(1+x)≈ex-1≈x

由于用多项式表示的函数，只要对自变量进行有限次加、减、乘三种算术运算，便能求出它的函数值来，因此我们经常用多项式来近似表达函数。

泰勒公式就是将函数用多项式表达的一种通用方法，又称为泰勒展开、泰勒级数，是将一个在x=x0处具有n阶导数的函数f（x）利用关于（x-x0）的n次多项式来逼近函数的方法。

二、泰勒中值定理1

定理：如果函数(x)在x0处具有n阶导数，那么存在x0的一个邻域，于该邻域内的任一x，有：

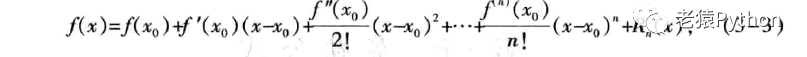
其中：Rn(x) = o((x-x0)n)                                                      (3-4)

具体证明的介绍请参考《理解泰勒中值定理1的证明过程的两个影响理解的简单隐含推导》的介绍。

说明：

多项式(3-3)公式右边去除“+Rn(x)”部分用pn（x）来表示：

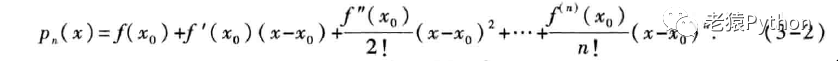
称pn（x）为函数f(x)在x0处(或按(x-x0)的幂展开)的n 次泰勒多项式。

公式(3-3)本身称为f(x)在x0处(或按(x-x0)的幂展开)的带有佩亚诺(Peano)余项的n 阶泰勒公式，而Rn(x)的表达式(3-4)称为佩亚诺余项，它就是用 n 次泰勒多项式来近似表达f(x)所产生的误差，这一误差是当x一>x0时(x-x0)n的高阶无穷小，但不能由它具体估算出误差的大小。

二、泰勒中值定理2

定理：如果函数f(x)在x0的某邻域U(x0)内具有n+1阶导数，那么对于任意x∈U(x0)，有：

其中：

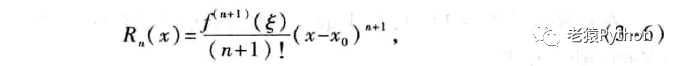
这里ε是x0与x之间的某个值。

证明思路：

Rn(x)具有n+1阶导数；

Rn(x0)和Rn(x)在x0位置的n阶导数值都为0；

Rn(x)和（x-x0）n+1在区间[x0,x]上满足柯西中值定理的要求，则

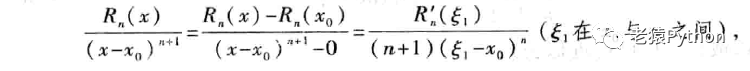
再对Rn’(x)与(n+1)(x-x0)n应用柯西中值定理，得：

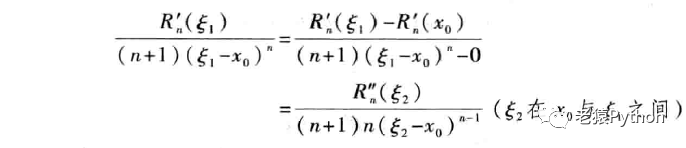
照此方法继续下去，经过（n+1）次后，得：

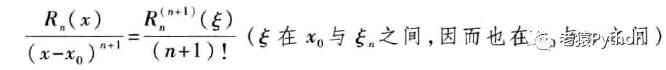
同时显然 Rn(n+1)(x) = f(n+1)(x)，从而可以证明定理成立。

说明：

公式(3-5)称为f(x)在x0处(或按(x-x0)的幂展开)的带有拉格朗日余项的n阶泰勒公式，而Rn(x)的表达式(3-6)称为拉格朗日余项。当n=0时，泰勒公式(3-5)变成拉格朗日中值公式：

f(x) = f(x0)+f’(ε)(x-x0) ，其中 ε∈（x0,x）

因此，泰勒中值定理2是拉格朗日中值定理的推广。

由泰勒中值定理2可知，以多项式pn(x)近似表达函数f(x)时，其误差为|Rn(x)|。如果对于某个固定的n，当x∈U(x0)时，|f(n+1)(x)|≤M，那么有估计式：

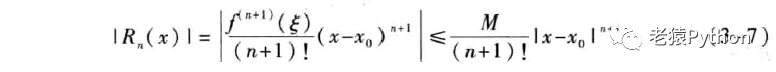
在泰勒公式(3-3)中，如果取x0=0，那么有带有佩亚诺余项的麦克劳林（Maclaurin）公式：

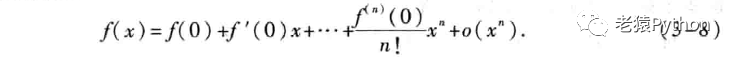
在泰勒公式(3-5)中，如果取x0=0，那么ε在0与x之间。因此可以令ε=θx(0<θ<1)，从而泰勒公式(3-5)变成较简单的形式，即所谓带有拉格朗日余项的麦克劳林公式：

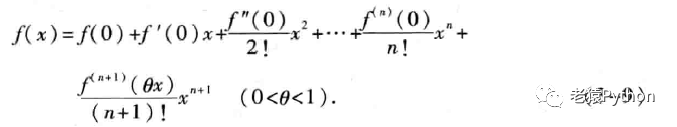
由(3-8)或(3-9)可得近似公式：

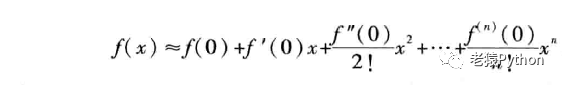
误差估计式(3-7)相应地变成：

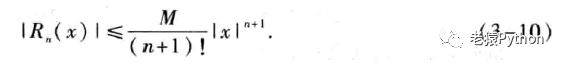
三、部分函数的泰勒公式表示

1、e的x次方泰勒公式

带拉格朗日余项的麦克劳林公式：

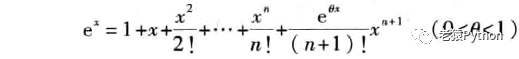
n次泰勒多项式为：

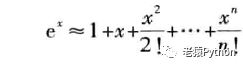
2、sinx的泰勒公式

带拉格朗日余项的麦克劳林公式：

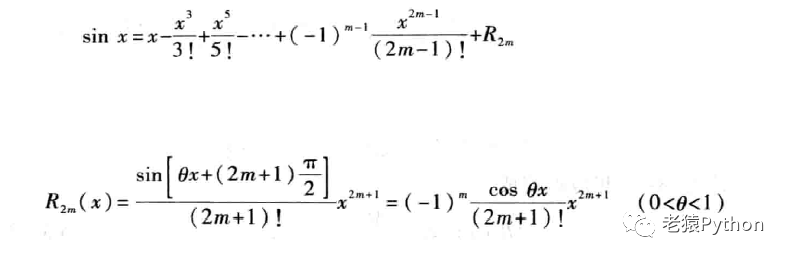
3、cosx的泰勒公式

带拉格朗日余项的麦克劳林公式：

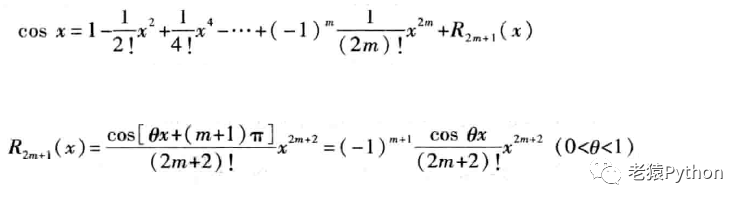
4、ln(1+x)的泰勒公式

带拉格朗日余项的麦克劳林公式：

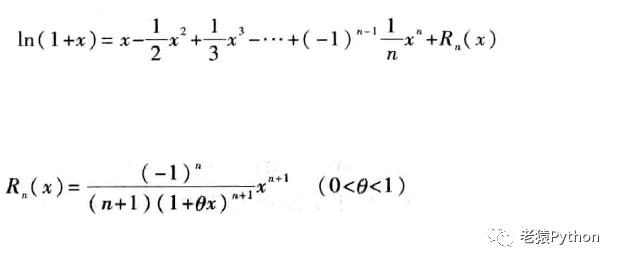
5、(1+x)的α次方的泰勒公式

带拉格朗日余项的麦克劳林公式：

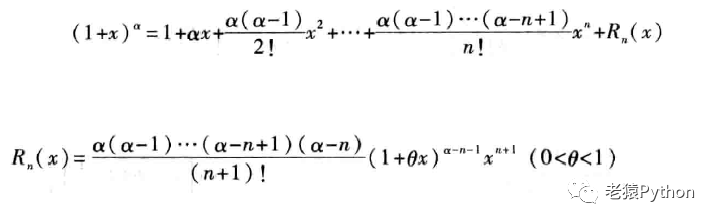
四、应用

五、小结

本文介绍了2个泰勒中值定理，泰勒中值定理1是将在某点具有n+1阶导数的函数表示为一个多项式加个余量的形式，泰勒中值定理2则将泰勒中值定理1的余量进行了细化。通过拉格朗日余项的n阶泰勒公式和带有拉格朗日余项的麦克劳林公式，可以将一个函数表示成n项的n阶多项式，从而为函数后续的运算提供便利。

说明：

本文内容是老猿学习同济版高数的总结，有需要原教材电子版以及OpenCV、Python基础知识、、图像处理原理介绍相关电子资料，或对文章内有有疑问咨询的，请扫博客首页左边二维码加微信公号，根据加微信公号后的自动回复操作。