关于泰勒公式展开

Taylor's Formula！

最近看书，看到泰勒公式展开，对它没有太大的印象，于是写一篇文章，整理一下个人对泰勒公式的理解吧！

先思考🤔一下，泰勒公式展开做的是什么？

对于某个函数(如)，是否可以用该函数的一个点，以及该函数的导数去表示。

先做一个假设，有这么一个点a 使得   (1)

首先，把a点代入 (1)式子中得到，

接着对 (1)式子两边⚽️求一次导数，并代入a这个数值得到，

接着对 (1)式子两边⚽️求两次导数，并代入a这个数值得到，

接着对 (1)式子两边⚽️求三次导数，并代入a这个数值得到，

接着对 (1)式子两边⚽️求四次导数，并代入a这个数值得到，

......

接着对 (1)式子两边⚽️求n次导数，并代入a这个数值得到，

通过以上多次求导，把的解带入(1)式子中，得到

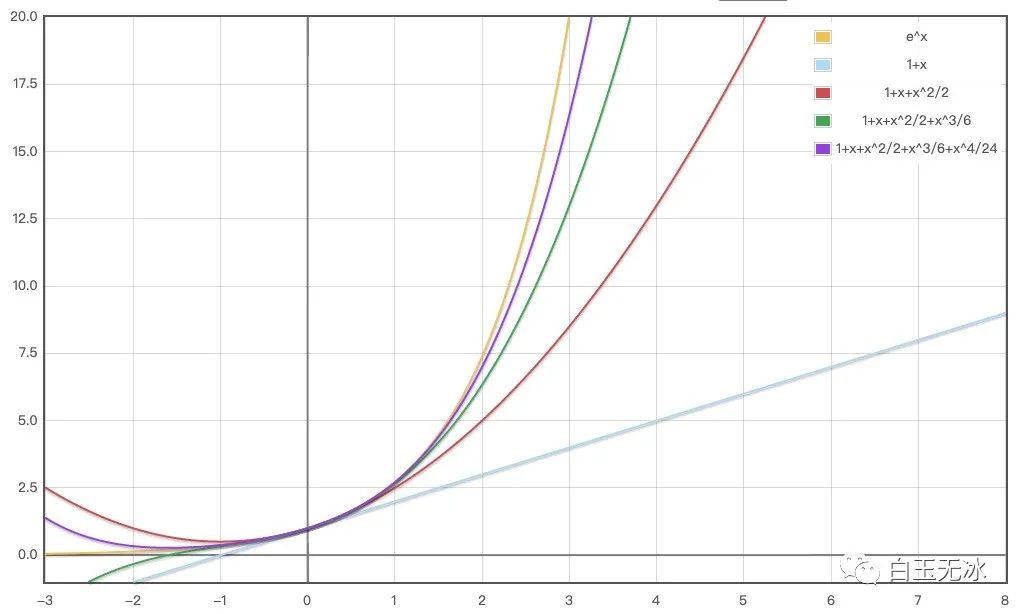
把上面的想法💡综合一下就是 泰勒近似定理

泰勒近似定理： 若在 光滑，则在所有次数为或更低的多项式中，当 在 附近时，最近似于 的是

经过一系列计算，我们得到了一个近似值，

那我们再给其补一个值，把近似值换成等于号！

假设，现在我们去求 。

我们先构造一个关于的函数，(2-1)式

• 把 代入 可以得到

• 把 代入 可以得到

根据中值定理，如果连续函数在区间内有零点，那么肯定可以在该区间找到一个值，其导数为 。

也就是说 存在一个使得 。

我们再构造一个函数

对于函数：

根据中值定理，存在一个使得 。

我们再构造一个函数

对于函数：

根据中值定理，存在一个使得 。

....

再构造n次函数 对于函数：

根据中值定理，存在一个使得 。

也就是 (3)式

注意到 ，(的最高次数为N,所有求(N+1)次导数，必然为0)，所以(3)式可求得

把上面的推导综合起来就是泰勒定理。

泰勒定理： 关于的N阶余项 ，其中c是介于x与a的一个数。于是可以写成

以上为白玉无冰关于 "泰勒公式展开" 的理解分享，如有错误欢迎指出，有任何想法，欢迎讨论！

点击“阅读原文”查看精选导航