Python中概率累计分布函数(CDF)分析
 PDF、CDF、CCDF图的区别
PDF、CDF、CCDF图的区别
PDF:连续型随机变量的概率密度函数是一个描述这个随机变量的输出值,在某个确定的取值点附近的可能性的函数。
概率密度函数,描述可能性的变化情况,比如正态分布密度函数,给定一个值, 判断这个值在该正态分布中所在的位置后, 获得其他数据高于该值或低于该值的比例。
CDF:能完整描述一个实数随机变量x的概率分布,是概率密度函数的积分。随机变量小于或者等于某个数值的概率P(X<=x)即:F(x) = P(X<=x)。
可使用 CDF 确定取自总体的随机观测值将小于或等于特定值的概率。还可以使用此信息来确定观测值将大于特定值或介于两个值之间的概率。
对于所有实数x,CDF(cumulative distribution function),与概率密度函数PDF(probability density function)相对。任何一个CDF,是一个不减函数,累积和为1。累计分段概率值就是所有比给定x小的数在数据集中所占的比例。任意特定点处的填充x的 CDF 等于 PDF 曲线下直至该点左侧阴影面积。
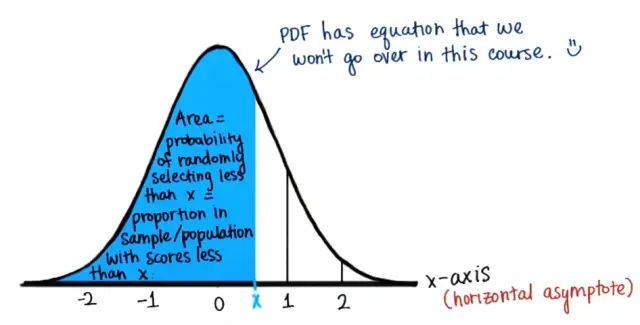
←概率密度函数PDF→
图中阴影面积=随机选择一个小于x的值的概率=总体中小于x的所有值所占比例
上面的pdf描述了CDF的变化趋势,即曲线的斜率。
CCDF:互补累积分布函数(complementary cumulative distribution function),是对连续函数,所有大于a的值,其出现概率的和。CDF 曲线从 0% 的概率上升到 100% 的概率,而 CCDF 曲线则从 100% 的概率下降到 0% 的概率。
累积分布函数(CDF)=∫PDF(曲线下的面积 = 1 或 100%)。
互补累积分布函数(CCDF)= 1-CDF。
import numpy as np
from scipy.stats import norm
import matplotlib.pyplot as plt
# 均值10,方差1,正态分布模拟数据
data = np.random.normal(10, 1, 100)
#计算正态概率密度函数在x处的值
def norm_dist_prob(theta):
y = norm.pdf(theta, loc=np.mean(data), scale=np.std(data))
return y
#计算正态分布累积概率值
def norm_dist_cdf(theta):
y = norm.cdf(theta,loc=10,scale=1)
return y
#利用ppf找到适合的横坐标,百分点函数
#ppf分位点函数(CDF的逆)即累计分布函数的逆函数(分位点函数,给出分位点返回对应的x值)。
#scipy.stats.norm.ppf(0.95, loc=0,scale=1)返回累积分布函数中概率等于0.95对应的x值(CDF函数中已知y求对应的x)。
x = np.linspace(norm.ppf(0.01,loc=np.mean(data), scale=np.std(data)),
norm.ppf(0.99,loc=np.mean(data), scale=np.std(data)), len(data)) #linspace() 函数返回指定间隔内均匀间隔数字的 ndarray。
y1=norm_dist_prob(x)
y2=norm_dist_cdf(x)
plt.plot(x, y1,'g',label='pdf')
plt.plot(x, y2,'r',label='cdf')
plt.show()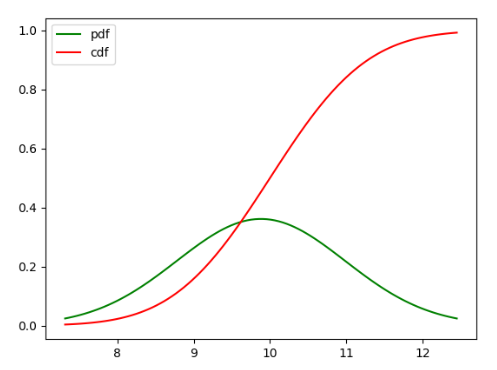
←PDF与CDF分布曲线对比→
 Python中计算累积分布函数
Python中计算累积分布函数
利用某设备三种工况条件下监测时间序列数据,对比分析不同工况下设备运行性能差异。这里数据大家可自行构造测试。
#CDF数据处理
def Cumsum_cdf(DATA):
denominator = len(DATA['VALS'])
Data1 = pd.Series(DATA['VALS'])
# #利用value_counts方法进行分组频数计算
Fre=Data1.value_counts()
# #对获得的表格整体按照索引自小到大进行排序
Fre_sort=Fre.sort_index(axis=0,ascending=True)
# # 每个数据出现频数除以数据总数才能获得该数据的概率
# #重置表格索引
Fre_df=Fre_sort.reset_index()
# #将频数转换成概率
Fre_df['VALS']=Fre_df['VALS']/denominator
# #将列表列索引重命名
Fre_df.columns=['Rds','Fre']
# # 将数据列表从小到大排列,然后将每个数据出现的概率进行叠加
# #利用cumsum函数进行概率的累加并按照顺序添加到表格中
Fre_df['cumsum']=np.cumsum(Fre_df['Fre'])
return Fre_df
def Cumulative_Distribution_Function(DATA,VAL1 =300):
import matplotlib.pyplot as plt
from scipy.special import jn, jn_zeros
plt.rcParams['font.sans-serif'] = ['SimHei'] # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False # 用来正常显示负号
df_A1,df_A2,df_A3 = DATA
#cdf数据处理函数,添加三条曲线
Fre_A1 = Cumsum_cdf(df_A1[df_A1.VALS > 0])
Fre_A2 = Cumsum_cdf(df_A2[df_A2.VALS > 0])
Fre_A3 = Cumsum_cdf(df_A3[df_A3.VALS > 0])
# 创建画布,只有一张图,也可以多张
# plot = plt.figure()
fig, ax1= plt.subplots(figsize=(8, 4), dpi=200)
ax1.spines["right"].set_visible(False)
ax1.spines["top"].set_visible(False)
ax1.grid(ls="--", lw=0.25, color="#4E616C")
# 按照Rds列为横坐标,累计概率分布为纵坐标作图
#添加三条数据曲线
ax1.plot(Fre_A1['Rds'], Fre_A1['cumsum'], label=f'工况1', mfc="white", ms=5)
ax1.plot(Fre_A2['Rds'], Fre_A2['cumsum'], label=f'工况2', mfc="white", ms=5)
ax1.plot(Fre_A3['Rds'], Fre_A3['cumsum'], label=f'工况3', mfc="white", ms=5)
# # 图的标题
ax1.legend(loc='upper left',
frameon=False,
edgecolor="None",fontsize=8)
#峰值负载
upper_peak = max(Fre_A1['Rds'].max(),Fre_A2['Rds'].max(),Fre_A3['Rds'].max())
f1_A25 = Fre_A3[Fre_A3['Rds'] / VAL1 >= 0.25]["cumsum"].to_list()[0]
f1_A50 = Fre_A3[Fre_A3['Rds'] / VAL1 >= 0.5]["cumsum"].to_list()[0]
# # 显示坐标点横线、竖线
peak = round(upper_peak/VAL1,2)*100
# # 峰值点负载率
ax1.annotate(
f"$({peak}$%$,100$%$)$", # 标注文字
(upper_peak,1),
# size="small",#medium
xytext=(-65, -40),
textcoords="offset points",
fontsize=10,
arrowprops=dict(
arrowstyle="->",
connectionstyle="arc3,rad=-0.3"), )
#25%、50%分界线
plt.vlines(VAL1 * 0.25, 0,f1_A25, colors="c", linestyles="dashed")
plt.vlines(VAL1 * 0.5, 0, f1_A50, colors="c", linestyles="dashed")
#峰值线
plt.vlines(upper_peak, 0,1,colors="r", linestyles="dashed")
#添加阴影区域,工况1
X = Fre_A1['Rds'].tolist()
C = Fre_A1['cumsum'].tolist()
x = np.array([i for i in X])
plt.fill_between(x,C,where=(VAL1*0.5*0.8 < x) & (x< VAL1*0.5),facecolor='green')
#标注工况3,50%负载概率值
ax1.annotate(
f"$(50$%$,{round(f1_A50,2)*100}$%$)$", # 标注文字
(VAL1*0.5,f1_A50),
# size="small",#medium
xytext=(-65, -40),
textcoords="offset points",
fontsize=10,
arrowprops=dict(
arrowstyle="->",
connectionstyle="arc3,rad=-0.3"), )
#标注分界线名称
ax1.text(
VAL1 * 0.27, 0.10,
f'25%负载率界限',
va="top", ha="left",
size=8)
ax1.text(
VAL1 * 0.52, 0.10,
f'50%负载率界限',
va="top", ha="left",
size=8)
#主题名称
team_ = ax1.text(
x=0, y=ax1.get_ylim()[1] + ax1.get_ylim()[1] / 20,
s=f"Cumulative probability",
color="#4E616C",
va='center',
ha='left',
size=8
)
# 横轴名
ax1.set_xlabel("用电量(kWh)",fontsize =8)
plt.savefig(r".\test.png",bbox_inches="tight")
return plt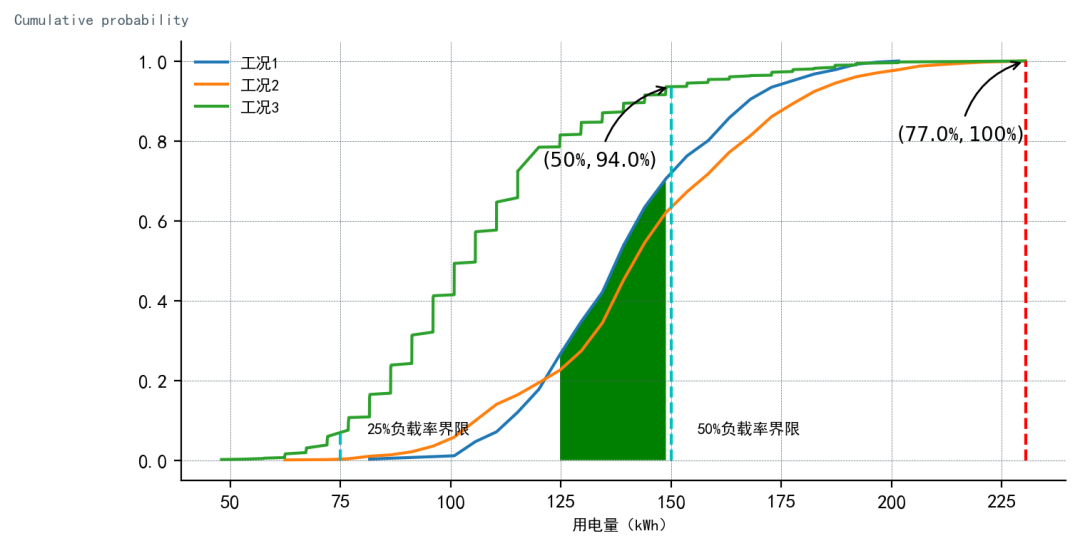
←某设备不同工况实际用能运行曲线对比→
利用 CDF(概率累积分布函数)分析数据集分布情况。分析概率分布函数曲线可以快速、简明地描述并量化由不同工况下导致的长期电能消耗中的细节差异。
注:
1、数据形式--dataframe
# 外部导入数据
DF = pd.read_excel(r".\ST\分析数据.xlsx")
df_A1 = DF[["工况1"]].copy()
df_A1 = df_A1.rename(columns={'工况1': 'VALS'})
df_A2 = DF[["工况2"]].copy()
df_A2 = df_A2.rename(columns={'工况2': 'VALS'})
df_A3 = DF[["工况3"]].copy()
df_A3 = df_A3.rename(columns={'工况3': 'VALS'})
DATA = df_A1,df_A2,df_A3VAL1 =300,VAL1这里表示设备功率值,其通常也作为异常参考阈值。这里不展开业务相关分析。
2、标注角度可按下图调整,更多.annotate()参数用法可上网查询。
3、图形美化自定义---参考以往推文一图胜千言,图解Matplotlib !
👆点击关注|设为星标|干货速递👆
评论
