【强化学习】DQN 的三种改进在运筹学中的应用
这篇文章主要介绍 DQN 的三种改进:Nature DQN、Double DQN、Dueling DQN 在运筹学中的应用,并给出三者的对比,同时也会给出不同增量学习下的效果。
这三种具体的改进方式可以从之前的文章中学习 《【强化学习】DQN 的各种改进》
背景
(搬运下背景)
假设有一个客服排班的任务,我们需要为 100 个人安排一个星期的排班问题,并且有以下约束条件:
一天被划分为 24 个时间段,即每个时间段为 1 个小时; 每个客服一个星期需要上七天班,每次上班八小时; 每个客服两次上班时间需要间隔 12 小时; 客服值班时,一个星期最早是 0,最晚 24*7 - 1。
评判标准:
现在有每个时间段所需客服人数,我们希望每个时段排班后的人数与实际人数尽量相近。
最优化问题可以使用启发式算法来做,上次用 DQN,这次用深度强化学习。
Nature DQN
之前给过 DQN 的代码,但是由于没有用批处理,所以速度非常慢,这里为了方便大家查看,给出完整版的 Nature DQN 代码,但是 Double DQN 和 Dueling DQN 的代码只会放上在前者需要修改的部分。
所以,Double DQN 的改进会加上 Nature DQN 的改进的部分,同理 Dueling DQN 实际上是 Nature DQN、Double DQN、Dueling DQN 三者的缝合怪。
import random
import numpy as np
import tensorflow as tf
from tensorflow.keras import layers
from copy import deepcopy
from collections import defaultdict, deque
random.seed(2020)
gpus = tf.config.experimental.list_physical_devices(device_type='GPU')
# GPU 随使用量增长
tf.config.experimental.set_memory_growth(gpus[0], True)
# 设定最大显存
tf.config.experimental.set_virtual_device_configuration(
gpus[0],
[tf.config.experimental.VirtualDeviceConfiguration(memory_limit=1024*16)]
)
person_n = 10
# 随机的一个排班需求
act_list = [5, 8, 8, 8, 5, 7, 9, 7, 5, 9, 7, 10, 10, 10, 7, 5, 10, 6, 7, 10, 7,
5, 6, 6, 10, 5, 9, 8, 8, 9, 9, 7, 6, 9, 7, 5, 9, 8, 7, 9, 10, 6, 7,
6, 6, 5, 8, 8, 9, 7, 8, 9, 8, 7, 7, 8, 9, 8, 7, 8, 9, 7, 10, 7, 5,
10, 10, 10, 7, 5, 6, 5, 9, 7, 5, 8, 7, 5, 5, 5, 7, 9, 9, 7, 9, 6, 9,
9, 9, 8, 9, 10, 5, 6, 6, 8, 7, 6, 5, 5, 9, 6, 7, 8, 6, 8, 9, 8, 5,
5, 8, 8, 6, 7, 9, 9, 10, 7, 8, 6, 6, 9, 6, 5, 6, 7, 5, 5, 8, 6, 5,
10, 10, 8, 10, 10, 6, 9, 8, 6, 5, 8, 6, 9, 8, 9, 6, 7, 6, 5, 9, 7,
7, 9, 6, 10, 7, 9, 5, 9, 9, 8, 7, 9, 9, 8, 8, 5]
class Env():
def __init__(self):
# 10 个人, 7 天,每个 bar 都可以向左向右移动,也可以不移动 '-1'
self.actions_space = ['{}{}L'.format(i, j) for i in range(person_n) for j in range(7)] + \
['{}{}R'.format(i, j) for i in range(person_n) for j in range(7)] + ['-1']
self.n_actions = len(self.actions_space)
self.act_list = act_list
self.w_list = [i / sum(self.act_list) for i in self.act_list]
self.state = [[i*24 for i in range(7)] for i in range(person_n)]
self.n_state = person_n * 7 * 24
self.punish = -1
print(self.act_list)
def list_2_str(self, l):
# 拼接完整的 list
state_list = [[0 for i in range(24*7)] for j in range(person_n)]
for person in range(person_n):
for i in l[person]:
for j in range(8):
state_list[person][i+j] = 1
return [i for state in state_list for i in state]
def reset(self):
self.state = [[i*24 for i in range(7)] for i in range(person_n)]
return self.list_2_str(self.state)
# 给当前排班打分,考虑权重
def reward(self, tmp_state):
# 判断每个人的排班要间隔 8+12 小时,否则 socre = -1000
for i in range(person_n):
# 星期天和星期一的排班间隔 8+12 小时
if (tmp_state[i][0] + (24*7-1) - tmp_state[i][6]) < 20:
return self.punish
for j in range(6):
if (tmp_state[i][j+1] - tmp_state[i][j]) < 20:
return self.punish
# 拼接完整的 list
state_list = [[0] * 24 * 7] * person_n
for person in range(person_n):
for i in tmp_state[person]:
for j in range(8):
state_list[person][i+j] = 1
plan_list = np.sum(state_list, axis=0).tolist()
s_list = [abs(plan_list[i] - self.act_list[i])/self.act_list[i] for i in range(len(plan_list))]
# 奖励越大越好,所以加个负号
score = 1-np.sum([s_list[i]*self.w_list[i] for i in range(len(s_list))])
return score
def step(self, action):
actions_str = self.actions_space[action]
if actions_str == '-1':
return self.list_2_str(self.state), self.reward(self.state)
else:
num = int(actions_str[0])
day = int(actions_str[1])
move = actions_str[2]
tmp_state = deepcopy(self.state)
if move == 'R':
if tmp_state[num][day] == (24*7-8-1):
tmp_state[num][day] = tmp_state[num][day] + 1
return self.list_2_str(tmp_state), self.punish
tmp_state[num][day] = tmp_state[num][day] + 1
if move == 'L':
if tmp_state[num][day] == 0:
tmp_state[num][day] = tmp_state[num][day] - 1
return self.list_2_str(tmp_state), self.punish
tmp_state[num][day] = tmp_state[num][day] - 1
reward = self.reward(tmp_state)
if reward == self.punish:
return self.list_2_str(tmp_state), self.punish
self.state = tmp_state
return self.list_2_str(self.state), self.reward(self.state)
class DQNAgent:
def __init__(self, state_size, action_size):
self.state_size = state_size
self.action_size = action_size
self.memory = deque(maxlen=2000)
self.discount_factor = 0.9
self.epsilon = 1.0 # exploration rate
self.epsilon_min = 0.1
self.epsilon_decay = 0.999
self.learning_rate = 0.01
# Nature DQN 就是创建了两个 DQN,防止又踢球又当裁判
self.model = self._build_model() # 用于选择动作、更新参数
self.model_Q = self._build_model() # 用于计算 Q 值,定期从 model 中拷贝数据。
def _build_model(self):
model = tf.keras.Sequential()
model.add(layers.Dense((512), input_shape=(self.state_size, ), activation='relu'))
model.add(layers.BatchNormalization())
model.add(layers.Dense((512), activation='relu'))
model.add(layers.BatchNormalization())
model.add(layers.Dense((256), activation='relu'))
model.add(layers.BatchNormalization())
model.add(layers.Dense((self.action_size), activation='sigmoid'))
model.compile(loss='mse', optimizer=tf.keras.optimizers.Adam(lr=self.learning_rate))
return model
def update_model_Q(self):
self.model_Q.set_weights(self.model.get_weights())
def memorize(self, state, action, reward, next_state):
self.memory.append((state, action, reward, next_state))
def get_action(self, state):
if np.random.rand() <= self.epsilon:
return random.randrange(self.action_size)
act_values = self.model.predict(state)
act_values = act_values[0]
max_action = np.random.choice(np.where(act_values == np.max(act_values))[0])
return max_action # returns action
def replay(self, batch_size):
minibatch = random.sample(self.memory, batch_size)
state_batch = [data[0] for data in minibatch]
action_batch = [data[1] for data in minibatch]
reward_batch = [data[2] for data in minibatch]
next_state_batch = [data[3] for data in minibatch]
next_state_batch = np.array(next_state_batch)
next_state_batch = next_state_batch.reshape(batch_size, self.state_size)
next_state_Q_batch = self.model_Q.predict(next_state_batch)
state_batch = np.array(state_batch)
state_batch = state_batch.reshape(batch_size, self.state_size)
state_Q_batch = self.model_Q.predict(state_batch)
y_batch = []
for i in range(batch_size):
target = reward_batch[i] + self.discount_factor * np.amax(next_state_Q_batch[i])
target_f = state_Q_batch[i]
target_f[action] = target
y_batch.append(target_f)
y_batch = np.array(y_batch)
y_batch = y_batch.reshape(batch_size, self.action_size)
self.model.fit(state_batch, y_batch, epochs=5, verbose=0)
if self.epsilon > self.epsilon_min:
self.epsilon *= self.epsilon_decay
def load(self, name):
self.model.load_weights(name)
def save(self, name):
self.model.save_weights(name)
env = Env()
bst_state = env.state
agent = DQNAgent(env.n_state, env.n_actions)
episodes = 1
update_model_Q_freq = 50
batch_size = 32
bst_reward = -500
for e in range(episodes):
state = env.reset()
print('---------- ', e, ' ------------')
for i in range(20000):
state = np.reshape(state, [1, env.n_state])
action = agent.get_action(state)
next_state, reward = env.step(action)
next_state = np.reshape(next_state, [1, env.n_state])
if i % update_model_Q_freq == 0:
agent.update_model_Q()
if reward != env.punish:
state = deepcopy(next_state)
agent.memorize(state, action, reward, next_state)
if len(agent.memory) > batch_size:
agent.replay(batch_size)
if bst_reward < reward:
bst_reward = reward
bst_state = deepcopy(env.state)
print('episode: {}/{}, i:{}, reward: {}, e: {:.2}'.format(e, episodes, i, bst_reward, agent.epsilon))
Double DQN
Double DQN 使用当前 Q 网络计算每一个 action 对应的 q 值,然后记录最大 q 值对应的 max action,然后用目标网络和 max action 计算目标 q 值。
em... 这块看公式比较清楚。
class DQNAgent:
... ...
def replay(self, batch_size):
minibatch = random.sample(self.memory, batch_size)
state_batch = [data[0] for data in minibatch]
action_batch = [data[1] for data in minibatch]
reward_batch = [data[2] for data in minibatch]
next_state_batch = [data[3] for data in minibatch]
# 修改了这里
next_state_batch = np.array(next_state_batch).reshape(batch_size, self.state_size)
cur_state_Q_batch = self.model.predict(next_state_batch)
max_action_next = np.argmax(cur_state_Q_batch, axis=1)
next_state_Q_batch = self.model_Q.predict(next_state_batch)
state_batch = np.array(state_batch).reshape(batch_size, self.state_size)
state_Q_batch = self.model_Q.predict(state_batch)
y_batch = []
for i in range(batch_size):
target = reward_batch[i] + self.discount_factor * next_state_Q_batch[i, max_action_next[i]]
target_f = state_Q_batch[i]
target_f[action] = target
y_batch.append(target_f)
y_batch = np.array(y_batch)
y_batch = y_batch.reshape(batch_size, self.action_size)
self.model.fit(state_batch, y_batch, epochs=5, verbose=0)
if self.epsilon > self.epsilon_min:
self.epsilon *= self.epsilon_decay
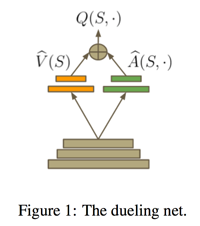
Dueling DQN
Dueling Network:将 Q 网络分成两个通道,一个输出 V,一个输出 A,最后再合起来得到 Q。
class DQNAgent:
...
def _build_model(self):
inputs = tf.keras.Input(shape=(self.state_size, ))
x = layers.Dense(512, activation='relu')(inputs)
x = layers.BatchNormalization()(x)
x = layers.Dense(512, activation='relu')(x)
x = layers.BatchNormalization()(x)
x = layers.Dense(256, activation='relu')(x)
x = layers.BatchNormalization()(x)
v = layers.Dense(1, activation='sigmoid')(x)
a = layers.Dense(self.action_size, activation='sigmoid')(x)
a = a - tf.reduce_mean(a)
outputs = a + v
model = tf.keras.Model(inputs=inputs, outputs=outputs)
model.compile(loss='mse', optimizer=tf.keras.optimizers.Adam(lr=self.learning_rate))
return model;
三者对比
放一下三者的对比:
| DQN | Nature DQN | Double DQN | Dueling Net | |
|---|---|---|---|---|
| 训练时长 | 32 | 31 min | 36 min | 38 min |
| 最好结果 | 0.6394 | 0.6538 | 0.6538 | 0.6538 |
| 收敛情况 | 9k 轮达到 0.6538 | 4.5k 轮达到 0.6538 | 8.5k 次达到 0.652; 1.3k 次达到 0.6538 |
PS:只实验了一次,结果仅供参考。
往期精彩回顾
本站知识星球“黄博的机器学习圈子”(92416895)
本站qq群704220115。
加入微信群请扫码:
评论
