数据分析——特征工程之特征关联
一、特征的相关矩阵
特征的相关矩阵
目标的相关矩阵
画出最相关的特征之间的关系
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
df = pd.read_csv('./data/train.csv')
corr_mat = df.corr()
f, ax = plt.subplots(figsize=(12, 9))
sns.heatmap(corr_mat, vmax=.8, square=True, ax=ax)
plt.show()
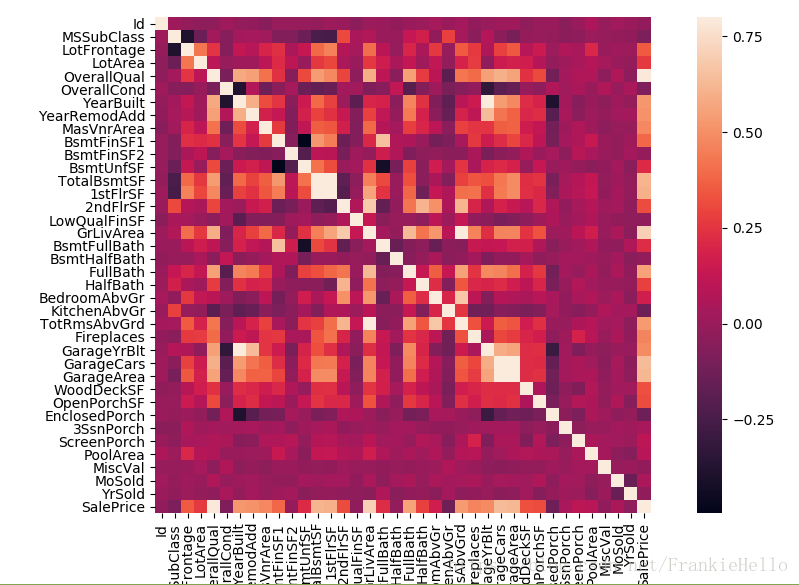
通过这个热力图,可以很直观的对各个特征之间的关系一目了然。另外,从图中可以看出TotalBsmtSF和1stFlrSF变量之间的相关性很明显,这就说明了如果同时使用这两个特征就会导致信息的冗余性,所以要尽量避免使用冗余的特征。
其中看一下df.corr()函数的源码:
def corr(self, method='pearson', min_periods=1):
"""
Compute pairwise correlation of columns, excluding NA/null values
Parameters
----------
method : {'pearson', 'kendall', 'spearman'}
* pearson : standard correlation coefficient
* kendall : Kendall Tau correlation coefficient
* spearman : Spearman rank correlation
min_periods : int, optional
Minimum number of observations required per pair of columns
to have a valid result. Currently only available for pearson
and spearman correlation
Returns
-------
y : DataFrame
"""
默认method参数是pearson,下面介绍下这三种相关系数:
1、Pearson correlation coefficient(皮尔逊相关系数)
皮尔逊相关系数用于度量两个变量X和Y之间的相关性(线性相关),它的值介于-1和1之间。
两个变量之间的皮尔逊相关系数定义为两个变量之间的协方差和标准差的商。
2、Kendall correlation coefficient(肯德尔相关性系数)
它所计算的对象是分类变量。
3、Spearman correlation coefficient(斯皮尔曼相关性系数)
它是衡量两个变量的依赖性的非参数指标。它利用单调方程评价两个统计变量的相关性,如果数据中没有重复值,并且两个变量完全单调相关时,斯皮尔曼相关系数则为+1或者-1。
二、目标的相关矩阵
找到与目标值相关性最大的几个特征,而这几个特征之间的相关性要低。
k = 10
cols = corr_mat.nlargest(k, 'SalePrice')['SalePrice'].index
cm = np.corrcoef(df[cols].values.T)
sns.heatmap(cm, annot=True, square=True, yticklabels=cols.values, xticklabels=cols.values)
plt.show()
通过以上代码得到与目标值相关性最大的前10个值,做出热力图。
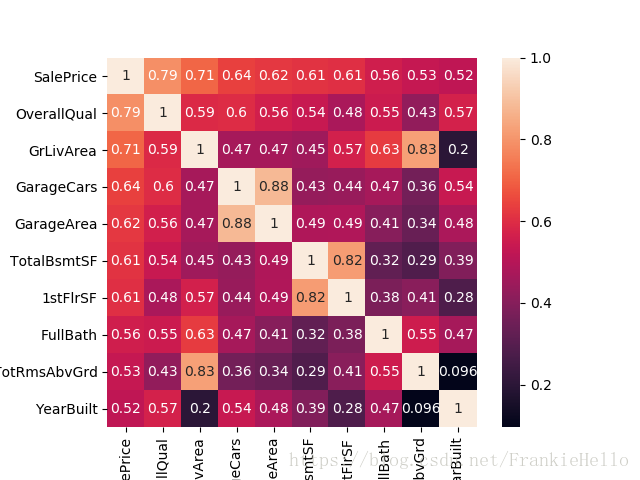
从图中可以很明显地看出OverallQual、GrLivArea等特征与SalePrice目标值之间有很大的关联。
三、最相关的特征之间的关系图
cols = ['SalePrice', 'OverallQual', 'GrLivArea', 'GarageCars', 'TotalBsmtSF', 'FullBath', 'YearBuilt']
sns.pairplot(df[cols], height = 2.5)
plt.show()
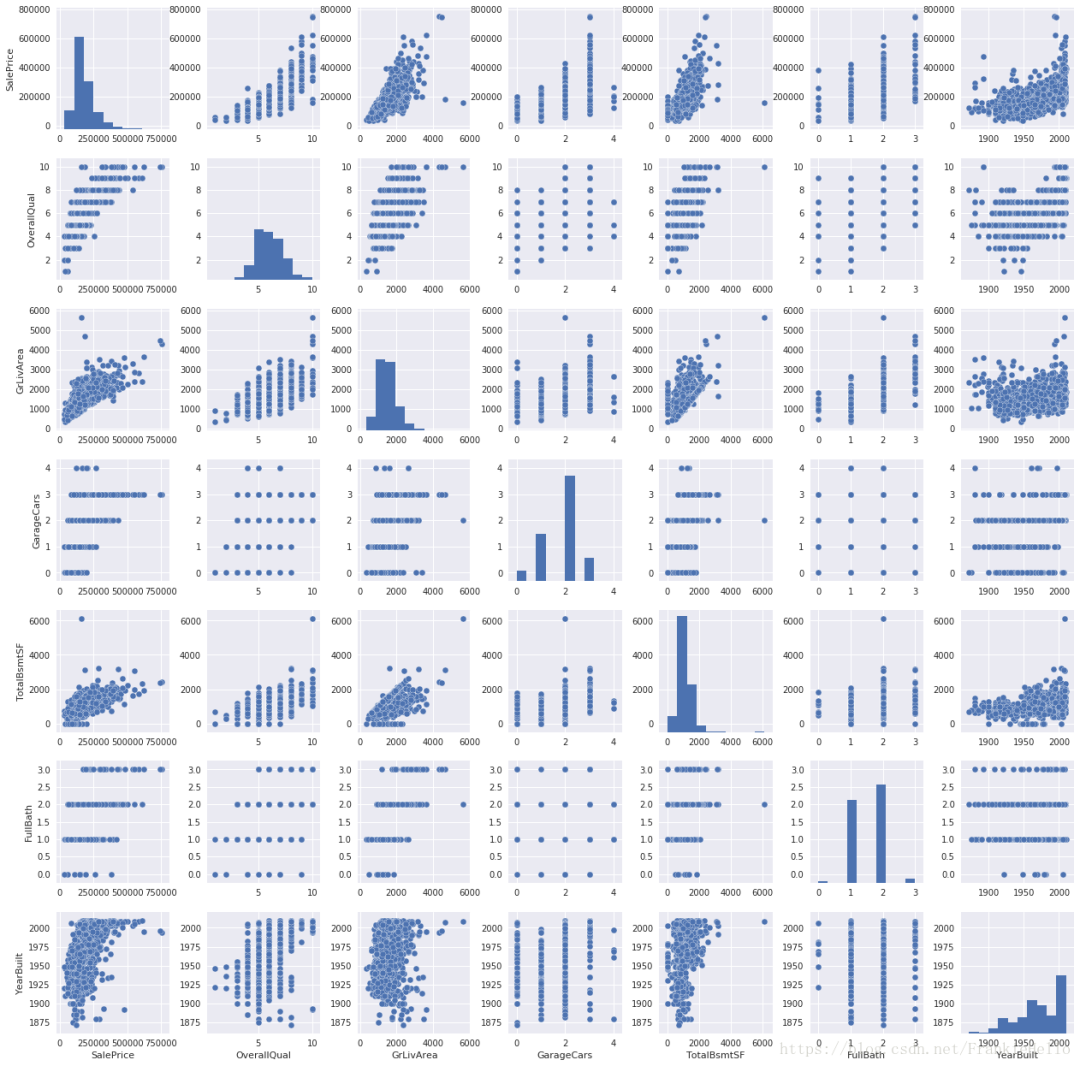
尽管我们已经知道了这些特征之间的一些关系,但是通过这个图可以给与一个更充分的理由。
《数据科学与人工智能》公众号推荐朋友们学习和使用Python语言,需要加入Python语言群的,请扫码加我个人微信,备注【姓名-Python群】,我诚邀你入群,大家学习和分享。
关于Python语言,有任何问题或者想法,请留言或者加群讨论。
